På tide med arbeidskrav 3.
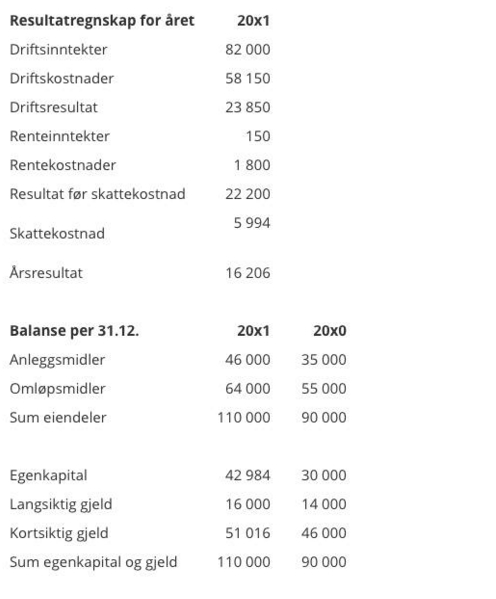
Vi tar utgangspunkt i disse tallene:
1. Hva var totalkapitalens rentabilitet før skatt for Tuscon Subsea AS i 20×1? Oppgi svaret (kun tallet) i hele prosent (avrund hvis nødvendig).
Rentabilitet er en metode for å måle resultatet i bedriften opp i mot investert kapital. Når vi måler rentabiliteten til totalkapitalen, slik vi skal i denne oppgaven, måler vi bedriftens avkastning på den samlede kapitalen som er bundet i bedriften. Totalkapitalrentabiliteten vil dermed gi oss et tall på nivået på bedriftens inntjening, og hvor godt man har “drevet butikken”. Eller med andre ord: hvor effektiv bedriften har vært til å forvalte de ressursene de har.
Totalkapitalrentabiliteten beregnes slik:
(Driftsresultat + finansinntekter) / gjennomsnittlig totalkapital
Når det gjelder gjennomsnittlig totalkapital så finner du denne ved å ta totalkapitalen fra fjoråret (IB) pluss totalkapitalen fra dette året (UB) og dele det på to. Totalkapitalen er sum eiendeler (aktiva) eller sum egenkapital og gjeld (passiva). Disse vet vi (jfr. balansen) at er det samme. For denne bedriften er IB totalkapital 90.000.000 og UB totalkapital…?
Nå er det bare å regne ut på kalkulatoren, så finner du svaret.
Når du ser på svaret, tenker du kanskje “er dette bra eller dårlig”?. Vel, det kommer blant annet an på hvor stor risiko virksomheten representerer, men den bør jo absolutt være høyere enn lånerenten. Altså bør vi for hver krone vi låner, tjene mer enn én krone.
Gjennomsnittlig totalkapitalrentabilitet for norske bedrifter i 2011 var 9,2%
2. Hva var egenkapitalens rentabilitet før skatt for Tuscon Subsea AS i 20×1? Oppgi svaret (kun tallet) i hele prosent (avrund hvis nødvendig).
Da vi regnet ut totalkapitalrentabiliteten (TKR) så vi hvordan den samlede kapitalen til bedriften forrentet seg. Nå skal vi se på egenkapitalens rentabilitet (EKR), som er veldig interessant for eierne og potensielle eiere av bedriften. Den viser hvordan eiernes investerte kapital utvikler seg. Dersom man står overfor en bedrift som er 100% finansiert av egenkapital (ingen gjeld), vil totalkapitalrentabiliteten og egenkapitalrentabiliteten være like stor. (Det er klare sammenhenger mellom EKR og TKR, og denne kan blant annet illustreres gjennom brekkstangformelen.) For deg som skal investere penger vil det kanskje være interessant å se hvilke av bedriftene du skal investere i som har høyest egenkapitalrentabilitet. Det som er viktig å huske er at eierne kommer sist når kapitalen skal fordeles. Først skal vareleverandørene, arbeidstakere, bankene osv. ha sine penger. Deretter, hvis det er noe til overs, går det til egenkapitalen.
Egenkapitalrentabiliteten bør som regel være høyere enn totalkapitalrentabiliteten. Dette fordi investorene som skyter inn pengene sine tar en mye høyere risiko enn f.eks. en produsent som selger en vare til bedriften. I tillegg bør den utvilsomt være bedre enn forventet avkastning på markedsporteføljen (f.eks. hovedindeksen på Oslo Børs). Dette fordi det er større risiko knyttet til å ha pengene sine i en virksomhet enn å ha pengene sine investert i hovedindeksen (mao mange bedrifter i forskjellige bransjer). Jo høyere risiko vi tar, jo høyere avkastning vil vi i sum kreve.
Vanligvis ønsker eierne å vite hvor mye av resultatet som går i deres “lomme”, derfor er det vanligste å beregne egenkapitalrentabiliteten etter skatt, men i denne oppgaven bes vi beregne den før skatt. Da er formelen slik:
ordinært resultat før skatt / gjennomsnittlig egenkapital
Gjennomsnittlig egenkapital får du ved å ta IB egenkapital + UB egenkapital og dele det på 2. UB egenkapital i våre tall er 42.984, og IB egenkapital er…?
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
3. Hvor mye ble avsatt til utbytte per 31.12.20×1? Oppgi svaret i hele tusen kroner (kun tallet), og bruk punktum som tusenskiller.
Hvis dere ikke har lært dere denne sammenhengen, så kan det hende dere syns BØK er litt håpløst. Denne ligninga får ofte mye til å løsne i dette faget:
IB + tilkomst – avgang = UB
For den som trenger å få det inn med teskje. Det denne ligninga sier er:
Så mye hadde jeg (IB) + så mye fikk jeg (tilkomst) – så mye ga jeg bort (avgang) = så mye har jeg igjen (UB).
Tilkomst er det som gjør at beholdningen/balanseposten blir større.
Avgang er det man kvitter seg med, og som følgelig gjør at beholdningen eller balanseposten blir mindre.
Denne kan også brukes her, og da må vi spørre oss selv, hva er “tilkomsten” og “avgangen” her?
Hvordan er det vi får tilkomst til egenkapitalen? Jo, egenkapitalen vokser hvis vi får et positivt resultat, og/eller hvis man får skutt inn egenkapital fra investorer.
Hvordan får vi “avgang”? Jo, egenkapitalen vil krympe hvis selskapet gir ut utbytte til eierne, eller ved underskudd i driften. Derfor blir sammenhengen slik:
IB EK + resultat + innskutt egenkapital – avsatt utbytte = UB EK
Løs denne ligningen med hensyn på avsatt utbytte.
Oppgaven sier ikke noe om innskutt egenkapital, så denne antar vi at er 0!
————-
Vi skal nå foreta ett ledd i det som kalles en likviditetsanalyse. Det er en analyse av betalingsevnen til en bedrift, altså bedriftens evne til å betale sine regninger i tide. Så vidt jeg kan se, skal dere ta for dere følgende “direkte” måter å beregne likviditeten til en bedrift på:
– Likviditetsgrad 1 (bør være større enn 2)
– Likviditetsgrad 2 (bør være større enn 1)
– Arbeidskapital
Det er viktig å presisere at man ikke får et fullstendig bilde ved å foreta disse analysene, da de er basert på balansen. Som vi vet gir balansen et uttrykk for en bedrifts finansielle situasjon på et gitt tidspunkt. Det kan gi et feilaktig bilde. Ta f.eks. en titt på likviditetsgradene til en av verdens største bedrifter, Coca Cola. Er likviditeten pr. definisjon god? Kanskje ikke. Er Coca Cola på randen av konkurs? Tvilsomt.
Det er viktig å se på andre faktorer, som f.eks. kredittider på gjeld og fordringer, nedbetalingstider, ubenyttet kassakreditt osv, osv…
4. Hva var endringen i arbeidskapitalen fra 20×0 til 20×1? Oppgi svaret (kun tallet) i hele tusen kroner og bruk punktum som tusenskiller. Har arbeidskapitalen blitt redusert, skal endringen angis med negativt fortegn.
Arbeidskapitalen er en viktig størrelse i regnskapet, og brukes ofte til å analysere likviditeten til en bedrift. Dette er kapital som en bedrift behøver for å finansiere varer og tjenester i arbeid inntil de er solgt og oppgjøret er på konto.
Formelen er slik:
Arbeidskapital = omløpsmidler – kortsiktig gjeld
Det vi kan lese ut fra denne sammenhengen er at hvis arbeidskapitalen er positiv (>0), er deler av omløpsmidlene finansiert av langsiktig gjeld eller EK. Dersom den er negativ (<0) er noe av anleggsmidlene finansiert av kortsiktig gjeld. En gylden regel er at de AM ikke skal være finansiert av KG. Er den det, og arbeidskapitalen følgelig negativ, er som regel likviditeten til bedriften også dårlig, og de vil ha problemer med å betale sine forpliktelser i tide.
Regn ut arbeidskapitalen for de to årene, og se hva endringen er.
5. Beregn likviditetsgrad 1 per 31.12.20×1. Oppgi svaret (tallet) med to desimalers nøyaktighet og uten benevning. Bruk komma som desimaltegn.
Likviditetsgrad 1 er et enkelt regnestykke. Man ser på forholdet mellom omløpsmidlene (bankinnskudd, fordringer, varelager osv.) og den kortsiktige gjelden. Altså:
L1 = omløpsmidler / kortsiktig gjeld
Her skal du bruke tallene for 20X1, ikke gjennomsnittet mellom IB og UB!
Litt om likviditetsgrad 2 i tillegg:
Likviditetsgrad 2 beregnes nesten likt, men tar utgangspunkt i våre mest likvide omløpsmidler – altså de omløpsmidlene som er penger, eller fort kan gjøres om til penger (eller til “likvider” som man sier når man skal være fancy). Dette betyr for alle praktiske formål omløpsmidler minus regnskapsført verdi på varelageret vårt. Dette ser vi i forhold til kortsiktig gjeld. Altså:
L2 = (omløpsmidler – varelager) / kortsiktig gjeld
6. Beregn egenkapitalprosenten per 31.12.20×1. Oppgi svaret (kun tallet) med to desimalers nøyaktighet.
Egenkapitalprosenten (også kalt egenkapitalandelen) viser hvor stor del av samlet kapital i bedriften som er egenkapital, altså hvor stor prosent av eiendelen som er finansiert med egne midler. Med andre ord viser dette hvor mye bedriften kan tape før det begynner å gå på bekostning av de vi har lånt penger av. Dette nøkkeltallet sier noe om bedriftens soliditet. Soliditeten til en bedrift forteller oss noe om hvor stor evne bedriften har til å tåle tap. Jo større prosent, desto mer solid er bedriften.
Formelen er slik:
Egenkapitalprosent = egenkapital / totalkapital
Totalkapitalen er, som jeg gjentar til det kjedsommelige, summen av dine eiendeler (aktiva) eller summen av din egenkapital og gjeld (passiva). De skal være like store, jfr. balansen. Ettersom det er 20X1 vi skal regne ut, bruker vi tallene fra 20×1 🙂
7. Bedriften har verdsatt sitt varelager meget forsiktig. Per 31.12.20×0 utgjorde skjulte reserver kr 4 000 000. Per 31.12.20×1 utgjorde skjulte reserver kr 4 700 000. Beregn korrekt driftsresultat for 20×1. Oppgi svaret i kroner (kun tallet). Bruk punktum som tusenskiller.
Mange syns dette med skjulte reserver er litt vanskelig, fordi boka forklarer det litt for komplisert for mange. Helt enkelt forklart er en skjult reserve en positiv forskjell mellom den virkelige verdien, og den balanseførte verdien av en eiendel. Man kan også få skjulte reserver i gjeld, men da hvis den virkelige gjelden er lavere enn den balanseførte.
Det vi kan resonere oss fram til er at dersom det viser seg at vi har lavere gjeld eller større verdi på anleggsmidler eller omløpsmidler enn vi trodde, vil dette påvirke egenkapitalposten i balansen vår. Egenkapitalen vil øke.
De oppgavene dere får er ofte sammensatt av informasjon om skjulte reserver over x antall år, og viser hvordan den skjulte reserven øker, synker eller forholder seg lik over tid. Det som er viktig å merke seg da er at hvis en skjult reserve forholder seg uendret fra et år til et annet, vil ikke dette påvirke resultatet. Dette fordi økningen av egenkapitalen er like stor ved inngangen som utgangen av året. Hvis vi ser en reduksjon i skjulte reserver vil det reelle resultatet være dårligere enn det fremstår. Hvis vi ser en økning (slik i vår oppgave) i skjulte reserver er det reelle resultatet bedre enn det som fremstår i regnskapet.
Så, det var teorien. Hvordan skal vi løse slike oppgaver? Jo, det finnes en veldig enkel fasit, og den er som følger (VIKTIG, kommer ofte på eksamen!):
Skjulte reserver UB 20×0 = 4.000.000
Skuljte reserver UB 20×1 = 4.700.000
Endring skjulte reserver = 700.000 (økning)
Bokført driftsresultat 20×1= ???
Endring i skjulte reserver = ???
Virkelig driftsresultat 20×1 = ???
8. Du får følgende opplysninger om en bedrift:
Totalkapitalens omløpshastighet er 4.
Resultatgraden er 3%.
Gjennomsnittlig gjeldsrente er 5%.
Total gjeld utgjør 15 mill.kr.
Egenkapitalen utgjør 30 mill.kr.
Hva er egenkapitalens rentabilitet? Oppgi svaret i % (kun tallet) med en desimals nøyaktighet. Bruk komma som desimaltegn.
Denne fremstår kanskje som litt krevende, men det er ved å løse slike oppgaver at det ofte går opp et lys eller to. La oss systematisere informasjonen noe:
Altså:
-Totalkapitalens omløpshastighet er 4.
*Forteller oss at den investerte kapitalen blir omsatt 4 ganger i løpet av et år. Formelen for totalkapitalens omløpshastighet er:
salgsinntekt / gjennomsnittlig totalkapital
-Resultatgraden er 3%.
*Forteller oss hvor stor del som tilfaller selskapet av hver krone som omsettes. Mao, hvor stor lønnsomheten er i forhold til de totale inntektene.
Formelen er: ordinært resultat før skatt + rentekostnad / salgsinntekt
-Gjennomsnittlig gjeldsrente er 5%.
*Forteller oss at vi i snitt betaler 5% rente på våre lån.
Formelen for gjennomsnittlig gjeldsrente er: rentekostnad/gjennomsnittlig gjeld
-Total gjeld utgjør 15.000.000
-Egenkapitalen utgjør 30.000.000
* Summen av total gjeld og egenkapital forteller oss at totalkapitalen er på 45.000.000 kroner. Totalkapitalen er jo som kjent summen av våre eiendeler (aktiva) eller vår egenkapital og gjeld (passiva)
Når jeg da i tillegg presenterer følgende formel, som kalles brekkstangformelen (viktig å lære, kommer ofte tekstspørsmål om denne på eksamen OBSOBS! Les side 454-455 i Økonomistyring 1-boka (Sending)), så blir dette kanskje lettere enn vi hadde trodd.
Brekkstangformelen:
EKR = TKR + (TKR – GGR) * G/EK
Hvor:
EKR = egenkapitalrentabiliteten
TKR = totalkapitalrentabiliteten
GGR = gjennomsnittlig gjeldsrente
G/EK = gjeld/egenkapital
Nå har vi en ligning med to ukjente (TKR og EKR). Hvis vi da retter vårt blikk til side 450 i Sending-boka, ser vi på DuPont-modellen at totalkapitalrentabiliteten fremkommer som et produkt av kapitalens omløpshastighet og resultatgraden. Med andre ord finner vi TKR ved å ta:
Kapitalens omløpshastighet * resultatgraden = 4 * 3% = 4*0,03 = 0,12
Nå er brekkstangformelen plutselig bare med én ukjent, nemlig EKR, så da er det bare å regne ut.
9. En bedrift har anskaffet et varig driftsmiddel for kr 1.200.000 inklusive mva. Forventet levetid for driftsmiddelet er 5 år. Anslått salgsverdi ved utløpet av levetiden er kr 100.000 inklusive mva. Anta at bedriften benytter lineære avskrivninger. Hva blir avskrivningene i år tre? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.
Hva er en avskriving? Det enkleste er å se på det som en slags periodisering av kostnadene knyttet til en stor investering som du “forbruker” over tid. F.eks. hvis du kjøper et anleggsmiddel i form av en maskin du skal bruke til produksjonen, er det feil å sette av hele denne utgiften i det året du kjøpte den. Du fordeler utgiften som kostnad over dens levetid.
Det finnes flere måter å beregne avskrivinger på, og det er opp til hver enkelt bedrift å avgjøre hvilken metode som er mest fornuftig for deres investeringer. De metodene vi kommer borti i dette faget er:
Lineær avskriving. Lineær avskrivingsmetode betyr at avskrivingen skal være den samme hvert år.
Saldoavskriving: Hvert enkelt år avskrives med en konstant prosentandel av det som er bokført verdi av f.eks maskinen ved årets begynnelse (01.01.XXXX). Denne metoden innebærer, i motsetning til lineær avskriving at avskrivingene vil bli lavere for hvert år, siden bokført verdi hele tiden reduseres etter hvert som driftsmiddelet avskrives.
I tillegg til disse har du også produksjonsenhetsmetoden, som tar hensyn til at driftsmidlets verdiforringelse skyldes bruken av det, og ikke så mye av “tidens tann”.
I denne oppgaven får du oppgitt at bedriften bruker lineær avskrivingsmetode. Vi får oppgitt at forventet levetid er 5 år (altså skal de fordele kostnadene over 5 år). Når de fem årene har gått, kommer den fremdeles til å ha en markedsverdi på 100.000 (80.000 eks mva) – altså er den ikke “helt oppbrukt”.
Da må du rett og slett finne ut hva den årlige avskrivingssummen er. Den er som sagt den samme hvert år når man benytter lineær avskriving.
Formelen for lineære avskrivninger er
(Anskaffelseskost – utrangeringsverdi) / forventet levetid
Husk at summene skal være eks mva. Du skal jo ikke avskrive momsen. Vil du lære mer om mva-regning, har jeg skrevet et innlegg om det her: http://hobbyokonomen.blogg.no/1442513016_17092015.html
10. En bedrift har anskaffet et varig driftsmiddel for kr 1.200.000 inklusive mva. Forventet levetid for driftsmiddelet er 5 år. Anslått salgsverdi ved utløpet av levetiden er kr 100.000 inklusive mva. Anta at bedriften benytter saldoavskrivninger. Saldoavskrivningssatsen er satt til 40%. Hva blir avskrivningene i år tre? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.
Saldoavskrivingssatsene vil variere fra år til år. De vil bli mindre for hvert år, ettersom de baseres på en prosentsats av restverdien ved inngangen av året.
Generelt betyr det altså.
År 1: restverdi pr. 1.1 * saldosats = avskrivingsbeløp år 1
År 2: (restverdi år 1 – avskrivingsbeløp år 1) * saldosats.
Et eksempel med tall:
Verdi varig driftsmiddel: 1.000.000
Prosentsats: 10%
År 1: 1.000.000 * 0,10 = 100.000 <—– Avskrivingsbeløpet i år 1 er altså 100.000
År 2: (1.000.000-100.000) * 0,10 = 90.000 <——- Verdien i år 2 er 900.000, og avskrivingssummen er derfor 90.000
År 3: (900.000-90.000) * 0,10 = 81.000 <—- Avskrivingssummen i år 3 er 81.000
Nå, prøv det samme med tallene i vår oppgave. Husk at også her må du trekke fra mva. på alle verdiene 🙂