Posted on 27.09.202019.04.2022

Pensjon

Jeg er fremdeles i 20-årene, og folk i min omgangskrets har frem til nå vært ganske lite opptatt av tema pensjon. Det er vel naturlig at studenter ikke tenker veldig mye på pensjon, med mindre man har en sterk interesse for privatøkonomi. Det gleder meg at flere av mine venner som nå er kommet i jobb etter studiene spør meg hvordan de bør tilpasse seg når det gjelder pensjon. Det er ikke bare bare å forklare pensjon, men jeg skal gjøre et ærlig forsøk i dette innlegget.

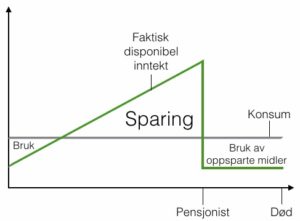
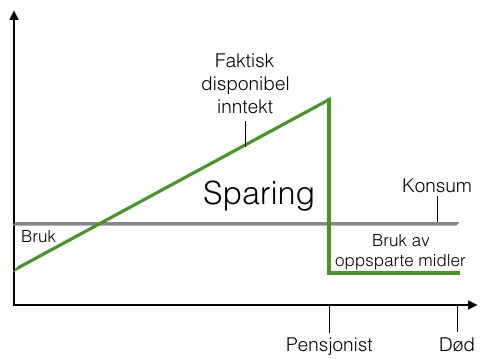
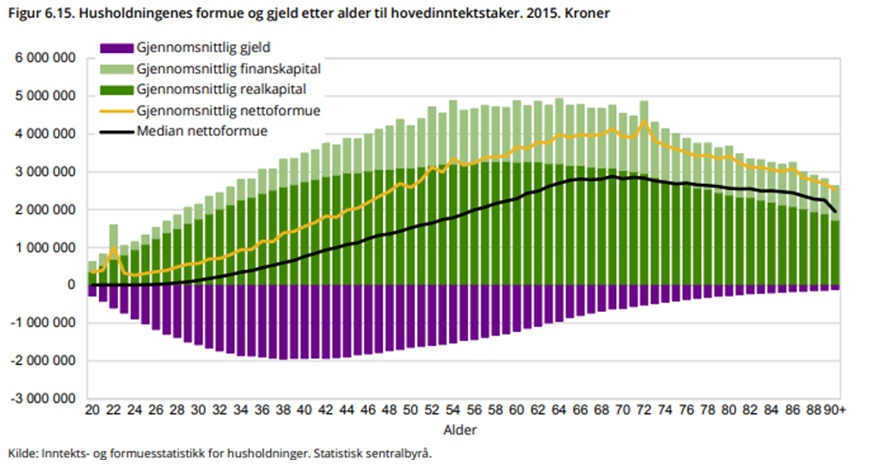
Pensjon er på mange måter en kombinasjon av de to finansielle verktøyene sparing og forsikring (risikostyring). I innlegget mitt om lån fortalte jeg at hovedårsaken til at vi låner penger er for å flytte konsum fra fremtiden til i dag. Pensjonssparing handler om det motsatte, nemlig å flytte konsum fra i dag til i fremtiden. Det er en absolutt nødvendighet dersom vi skal kunne fortsette å konsumere etter vår arbeidsinntekt forsvinner. Figuren under husker du kanskje hvis du har lest innlegget om lån. Figuren illustrerer fenomenet “konsumglatting”, nemlig at vi fordeler konsumet vårt over hele levetiden.

Livssylushypotesen (Modigliani), bilde hentet fra Hellebostad og Mauring

Vi har også et element av usikkerhet inn i bildet. Det er nemlig en risiko for at vi blir fryktelig gamle. Dersom vi blir eldre enn vi først antok, må vi kunne konsumere de siste leveårene også, og av den grunn består pensjon av et forsikringselement også.

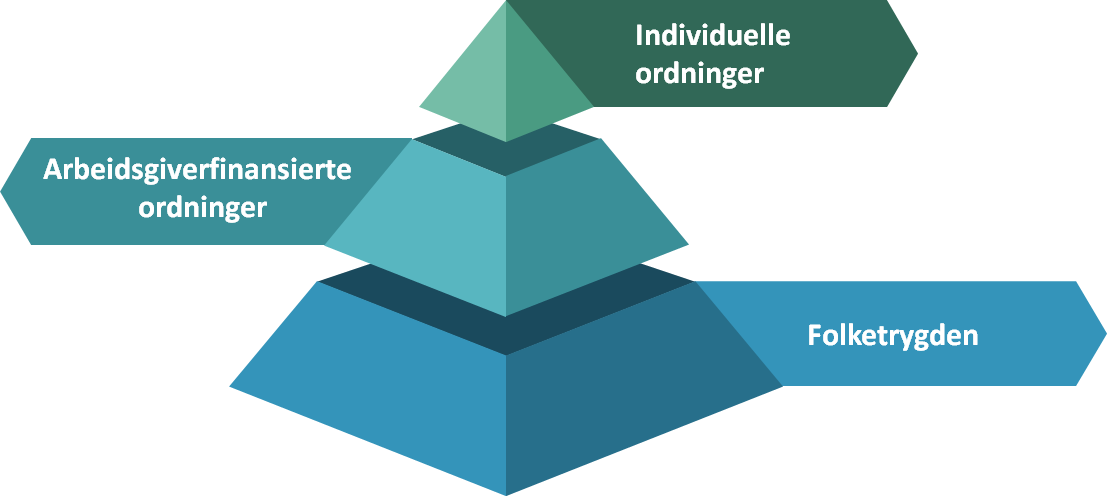
For å forstå pensjon kan vi ta utgangspunkt i de tre nivåene i “pensjonspyramiden”:

Det nederste nivået er folketrygden. Folketrygden er obligatorisk for alle ved at innbetaling skjer som en del av skatten (gjennom trygdeavgift og arbeidsgiveravgift), og skal sikre alle en “rimelig pensjon”.

Det midterste nivået er arbeidgiverfinansierte ordninger. I motsetning til folketrygden er dette nivået forskjellig fra person til person, eller riktigere sagt fra arbeidsgiver til arbeidsgiver. Arbeidsgiver står nemlig fritt til å velge pensjonsordning selv for den ansatte, innenfor lovverkets (eventuelt tariffavtalenes) rammer.

Det øverste nivået er den delen av pensjonen vi frivillig sørger for selv. Her står man helt fritt til å velge blant de sparings- og forsikringsordningene som eksisterer i markedet – eller man kan la være.

Jeg vil nå ta for meg hvert enkelt nivå fra bunn til topp, og starter med folketrygden.

Folketrygden er en ordning som involverer individene og staten (og for såvidt arbeidsgiver indirekte via arbeidsgiveravgiften). Folketrygden ble lagt om for noen år siden, og denne omleggingen fikk en del konsekvenser, særlig for de født etter 1963. Personer født før 1953 følger fremdeles den gamle ordningen for folketrygden. De født mellom 1954-1962 har en egen overgangsordning, mens de født etter 1963 følger den nye ordningen. Jeg skal fokusere på den nye ordningen, målgruppen tatt i betraktning.

Hovedprinsippene bak folketrygden er:

Man tjener opp 18,1% av lønnen som pensjonsopptjening, opp til 7,1G (tilsvarer ca 710.000 kroner i 2019/2020). Det som overskyter 7,1G gir ingen opptjening.
Det man har tjent opp reguleres med allmenn lønnsvekst i samfunnet. Det betyr at dersom det går bra i Norge, og vi har en høy lønnsvekst, så kommer det pensjonspengene til gode også.
Uttaket avhenger av et delingstall. Delingstallet er konstruert slik at det skal representere forvenet levetid fra du begynner å ta ut pensjonen. Delingstallet gjør systemet nøytralt med hensyn til når du begynner å ta ut pensjon fra ordningen, fordi du får et høyere delingstall jo tidligere du begynner uttaket.
Dersom du har lav opptjening, får man likevel en minimumspensjon (også kalt “minstepensjon”).

Du kan altså se for deg at for hver krone du tjener, går 18,1 øre inn på en konto. For hvert år justeres beløpet på “kontoen” med en “rente” tilsvarende lønnsveksten i samfunnet, før et beløp tilsvarende 18,1% av årets inntekt (opp til 7,1G) settes inn på kontoen. Etter du har begynt å ta ut penger, reduseres “avkastningen” på kontoen med 0,75 prosentpoeng. Det vil si at etter du har begynt å ta ut av ordningen, vil beløpet justeres med lønnsvekst fratrukket 0,75%. I perioder med lav lønnsvekst vil altså pensjonister kunne oppleve svekket kjøpekraft fra ett år til et annet (dersom inflasjon>lønnsvekst-0,75%). Så er det noen som spør seg om det er rettferdig, men det skal ikke vi dvele ved.

Fra du er 62 år kan du begynne å ta ut penger fra folketrygden. Du velger selv når du begynner å ta ut etter fylte 62, men jo tidligere du begynner å ta ut, jo lavere utbetaling får du per år. Hva du får utbetalt fra det året du starter uttak avgjøres av delingstallet for ditt årskull. Delingstallet finner du på nav.no. Delingstallene fastsettes slik at den samlede pensjonen man kan forvente å få ut av ordningen er lik uavhengig av når du begynner å ta ut penger. Delingstallet reflekterer derfor både muligheten for fleksibelt uttak (jo før, jo mindre per år) og levealdersjustering (jo lengre forventet levealder, jo mindre hvert år). En person født i 1970 kan altså forvente å få utbetalt mer hvert år enn en person født i 1990 selv om begge begynner å ta ut penger fra fylte 62. Dette fordi personen født i 1990 forventes å leve lengre, og derfor må fordele pengene over lengre tid.

Levealdersjusteringen er lik for kvinner og menn, noe som isolert sett er en fordel for kvinner, ettersom de statistisk sett har nesten fire år lengre levetid enn menn. Skulle systemet tatt hensyn til dette, ville kvinner få en lavere årlig pensjon for å oppnå den samme pensjonen over livsløpet. Dette syns enkelte menn er veldig urettferdig selvfølgelig, men man kan ikke se isolert på dette, og menn har ingen grunn til å sutre. Vi vet at kvinner i snitt tjener mindre enn menn (kvinner tjener ca 89% av det menn tjener), noe som fører til lavere pensjonsopptjening, både gjennom folketrygden og gjennom tjenestepensjon som jeg skal komme tilbake til senere. I snitt får menn utbetalt 28% mer pensjon enn kvinner i følge SSB.

Delingstallet for hvert årskull bestemmes endelig det året årskullet fyller 61 år. Selv om du er yngre enn 61 kan du allerede nå se hva prognosene sier vil bli dine delingstall (men det endelige delingstallet vil altså ikke bli fastsatt før det året du fyller 61). Jeg er født i 1993, og delingstallet mitt dersom jeg begynner å ta ut fra ordningen ved fylte 62 vil være 23,93. Dersom beholdningen min ved 62 er 1 million, blir mitt uttak: 1.000.000/23,93 = ca 41.788 per år. Hva viser delingstallet egentlig? Jo, det viser egentlig forventet gjenværende levetid fra uttakstidspunktet. Det forventes at jeg skal leve nesten 24 år fra fylte 62. Venter jeg derimot til jeg er 68 med å ta ut pensjon, får jeg delingstall 19,06, og får følgelig 52.466 kroner per år, altså 25,5% mer per år.

Merk dere at det ikke er slik at man må slutte å arbeide når man begynner å ta ut penger fra folketrygden. Du kan starte uttak fra 62, men fortsette å jobbe. Hva er smart å gjøre? Ta ut tidlig, eller ta ut sent? Dette er det ikke noe fasitsvar på, men man kan ta følgende med i vurderingen:

Er du i stand til å plassere din overskuddslikviditet i produkter/prosjekter som gir høy avkastning? I såfall kan det være gunstig å starte uttak tidlig.
Har du høy inntekt ved siden av uttaket? I såfall vil det kunne være gunstig å vente med å ta ut pengene frem til inntekten din går ned (pga trinnskatten skatter du mer ved høy inntekt).
Er du i formuesskatteposisjon? I såfall kan det være gunstig å vente, slik at du ikke trenger å betale formuesskatt på det du tar ut. Pensjonsbeholdningen er ikke formuesskattepliktig før den tas ut av pensjonsordningen.
Tror du at du kommer til å dø tidlig? I såfall kan det være greit å starte uttak tidlig. Statistisk sett vil menn leve kortere enn kvinner, og folk med lav utdanning og manuelle yrker vil leve kortere enn høyt utdannede.

Er det jeg skriver i siste kulepunkt rettferdig? Tja, noen hevder at det ikke er det, ettersom noen vil få lavere utbetaling enn andre. Se for eksempel for dere en lege og en renholdsarbeider som er født samme år, og er like lenge i arbeidslivet; legen vil sannsynligvis leve lengre enn renholdsarbeideren, og derfor få en større utbetaling fra folketrygden. Burde de som forventes å leve kortere kompenseres for dette i ordningen? På samme måte kan vi jo si at en ikke-røyker sannsynligvis vil få en større utbetaling enn en som røyker, selv om alt annet ved dem er likt. Vi kan vel alle være enige i at det ville vært ganske feil dersom ordningen skulle gitt incentiver til å begynne å røyke, ved at det gis høyere utbetaling til røykere.

Vi skal forlate folketrygden, og går over til arbeidsgiverfinansierte ordninger.

De arbeidsgiverfinansierte ordningene, ofte omtalt som tjenestepensjon, blir litt mer kompliserte – mye fordi det er mange flere parter inn i bildet. Folketrygden er en ordning mellom deg og staten. Arbeidsgiverfinansierte ordninger involverer i tillegg arbeidsgiver og forsikringsselskaper.

Av arbeidsgiverfinansierte ordninger, finnes det i all hovedsak to hovedgrupper innenfor produktene som tilbys. Dette er garanterte produkter, og ikke-garanterte produkter. I tillegg skiller man på produktene hvorvidt man er ansatt eller tidligere ansatt. Det finnes noen flere, men jeg fokuserer på de to vanligste, ytelsespensjon og innskuddspensjon, og med mest fokus på sistnevnte.

Forskjellen på garanterte og ikke-garanterte produkter er enkelt forklart at de garanterte produktene gir et bestemt pensjonsbeløp, mens ikke-garanterte produkter gir et innskudd til en “pensjonskonto”, hvor utbetalingen avhenger av innskuddet til kontoen og nettoavkastningen på innskuddsbeløpet. Når du avslutter ansettelsesforholdet hos en arbeidsgiver hvor du har hatt en ytelsespensjonsordning, vil ordningen gjøres om til en fripolise. Fripolisen definerer hvor mye penger du skal få ut av denne avtalen når du går av med pensjon. Når du avslutter ansettelsesforholdet hos en arbeidsgiver med innskuddspensjonsordning, gjøres ordningen om til et pensjonskapitalbevis, som igrunn er en oversikt over hva som står på “pensjonskontoen”.

Ytelsespensjon og fripolise

Ytelsespensjon blir mindre og mindre vanlig. De fleste private virksomheter har, eller er på vei over til, innskuddsbaserte ordninger. Årsakene til det er i stor grad at en ytelsesbasert ordning påfører arbeidsgiver veldig langsiktige forpliktelser. Stort sett er det bedrifter som leverer tjenester til det offentlige eller andre bedrifter som har forhandlet frem gode ordninger i tariffavtalen sin, som har ytelsespensjon. Den ytelsesbaserte ordningen samkjøres med folketrygdeopptjeningen slik at man ved full opptjening (typisk 30 år) skal være sikret en pensjon på X prosent (for eksempel 66%) av lønnen på fratredelsestidspunktet, forutsatt et uttak på et viss tidspunkt (typisk ved fylte 67 år). Det er mulig med tidligere uttak, men da går også ytelsen per år ned for å kompensere for lengre forventet uttakstid.

Offentlige ansatte har i dag veldig gode pensjonsordninger (bedre enn de fleste private virksomheter), og disse ordningene er ganske lik (men ikke helt lik) ytelsespensjonsordningen. Jeg går ikke nærmere inn på offentlig tjenestepensjon i dette innlegget. Likevel kan det være verdt å merke seg at selv om lønnsnivået i det offentlige i snitt kan være lavere enn hos private virksomheter, blir mye av dette kompensert av den gode offentlige tjenestepensjonsordningen. Husk at tjenestepensjon også er lønn, bare lønn du får litt senere i livet.

For å forklare ytelsespensjon veldig enkelt kan vi tenke oss at forvalteren av denne ordningen (typisk et forsikringsselskap) investerer pengene i finansielle instrumenter som gir avkastning. Avkastningen fordeles slik at kunden får sin garanterte avkastning. Eierne av forsikringsselskapet får en tilsvarende avkastning på egenkapitalen de har i selskapet. Avkastning utover garantert avkastning fordeles på eierne, kunden og noe som kalles bonusfond (penger som i utgangspunktet er satt av for å øke pensjonen til kunden, men som ennå ikke er fordelt eller på noen måte er garantert at blir fordelt). Det som er greit å vite her er at så lenge du er ansatt, er det arbeidsgiver som får eventuell overskytende avkastning utover garantiavkastningen, men når ansettelsesforholdet er avsluttet går det til fripolisen din.

Men hva er en fripolise? Jo, det er altså en tidligere ytelsespensjon. Når du slutter i jobben blir ytelsespensjonen flyttet fra arbeidsgiver og over på en konto som administreres på en ganske lik måte som ytelsespensjonen, altså garantert avkastning + deler av overskytende avkastning.

Innskuddspensjon og pensjonskapitalbevis

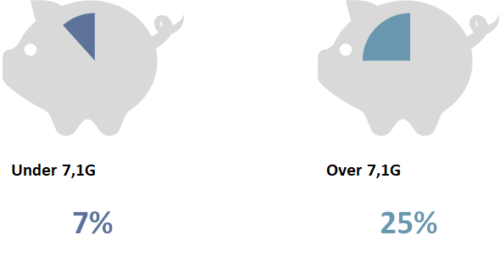
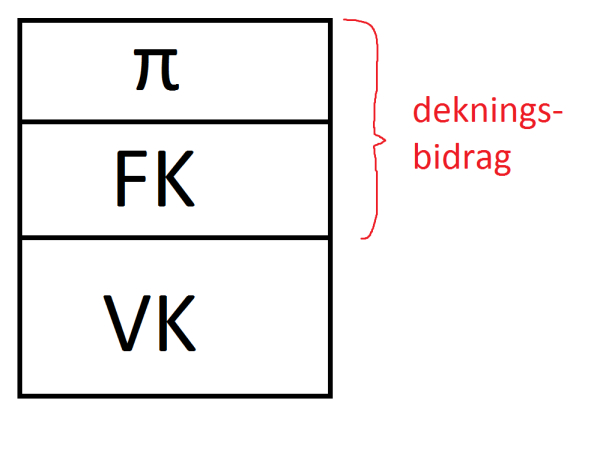
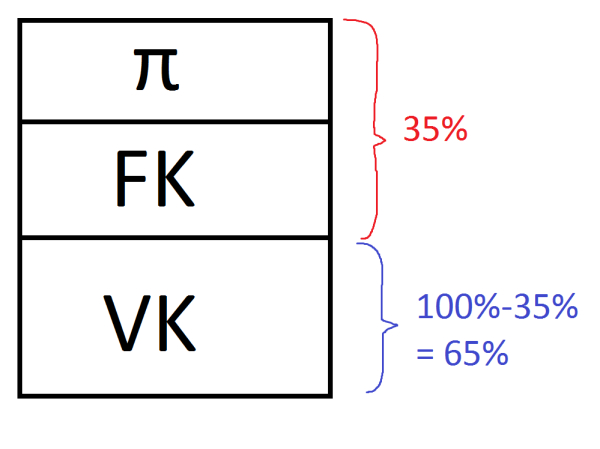
Innskuddspensjon er altså det vanligste i dag, og blir bare enda mer vanlig. Innskuddspensjon er et innskudd i prosent av lønnen din. Det kan være et innskudd fra første krone, eller det kan være et innskudd fra og med 1G. Lovens minstekrav er 2% av lønn mellom 1-12G. “Kjipe” bedrifter gir deg lovens minimum, mens andre har innskudd fra første krone, og vesentlig høyere enn 2% av lønnen (makssatsen er 7% for lønn under 7,1G og 25% for lønn over 7,1G, se figur lengre nede). Beholdningen av innskuddspensjonen øker altså jo mer du tjener, i tillegg til at den utvikler seg etter avkastningen på innskuddet. Det fungerer altså ganske likt en vanlig konto, bortsett fra at du selv får mulighet til å velge hvilken risiko du vil utsette innskuddet for. Du kan med andre ord selv bestemme hvordan innskuddspensjonen din skal investeres, eller som vi nerdene kaller det; du bestemmer innskuddspensjonens aktivaallokering. Det er en sannhet med noen modifikasjoner, fordi forsikringsselskapet har bare et utvalg alternativer du kan velge. Normalt kan du velge mellom ulike fond, eller enda mer vanlig får man velge hvor stor prosentandel av innskuddet du vil plassere i aksjer (hvorpå det resterende blir investert i typisk obligasjoner og andre lavrisikoinstrumenter). Jo lavere aksjeandel, jo lavere risiko, men jo lavere avkastning kan du forvente på innskuddspensjonen din.

Slutter du i jobben får man et pensjonskapitalbevis. Det som er viktig å huske er at for innskuddspensjonen er det arbeidsgiver som betaler forvaltningen av pengene, men for pensjonskapitalbeviset er det du selv som betaler forvaltningen. Fordi arbeidsgiver vanligvis ikke vil betale all verden for forvaltningen av dine penger, vil det normalt være flere investeringsalternativer for et pensjonskapitalbevis enn du hadde før du sluttet i jobben. At pensjonsforvalteren din som standard setter deg opp på en forvaltningsplan som er svindyr bør ikke komme som en overraskelse. Kanskje dette er dagen for å sjekke hva du betaler i forvaltningshonorar for ditt pensjonskapitalbevis?

Som sagt finnes det makssatser for innskudd. Det vil si, det er mulig å gi innskudd høyere enn dette, men det må skattes som lønn. Satsene er altså 7% opp til 7,1G, og 25% mellom 7,1G og 12G. Dette er omtrent de samme satsene som på ytelsespensjon (i gjennomsnitt). Det er en logikk i hvorfor det er høyere for lønn over 7,1G. Det må ses i sammenheng med det vi lærte tidligere om folketrygden. Folketrygden setter av et innskudd på 18,1% av lønn opptil 7,1G. Gapet mellom 7% og 25% er altså ment å kompensere for at det ikke settes av noe til folketrygden for lønn over 7,1G ved at det kan settes inn 18% mer i innskuddspensjon.

Så er det sikkert mange som lurer på hva som er best av ytelsespensjon og innskuddspensjon. Hovedforskjellen er; i en ytelsesbasert pensjonsordning vet du hva du vil få (ytelsen), mens med en innskuddsbasert pensjonsordning vet vi bare hva vi putter inn – og ikke hva vi vil få igjen. Det betyr ikke nødvendigvis at ytelsespensjon er best, selv om det nok er gjengs oppfatning. En annen forskjell er nemlig at ved innskuddspensjon er det arbeidsgiver og/eller du som bestemmer investeringsprofilen, mens for ytelsespensjon er det forsikringsselskapet (pensjonskapitalforvalteren) som bestemmer. Uten at jeg skal gå i dybden på hvordan utbetalingen av garanterte produkter (som en ytelsespensjon/fripolise) skjer, så kan du merke deg at for garanterte produkter så får man en utbetaling som tilsvarer et garantert beløp, med muligheten til å få noe mer dersom forsikringsselskapets avkastning på porteføljen er ekstra god. Det betyr at det ville vært veldig gunstig for kundene dersom forsikringsselskapet har høy risiko på porteføljen, ettersom økt risiko gir høyere forventet avkastning, noe som ville komme kundene til gode. Kundene har ingen nedsiderisiko ved en slik høy risiko, fordi de får jo sitt garanterte beløp uansett. For forsikringsselskapet gir imidlertid en slik ordning incentiver til å plassere porteføljen i svært sikre investeringer, ettersom de har mindre og vinne og mer å tape på å utsette seg for risiko. Ettersom det er forsikringsselskapet som bestemmer, blir det slik. Dette er også en del av kritikken knyttet til ytelsespensjon, nemlig at det ikke er optimalt for samfunnet at det tas så lav risiko i investeringen av pensjonsmidlene.

Hvis man ser helt rasjonelt på de to ordningene, så vil en ordning hvor pensjonsmidlene er investert i rene aksjefond være det mest optimale for kundene over tid, da dette gir høyest forventet pensjonsutbetaling. Dette er altså noe man ikke kan oppnå med ytelsesbasert pensjon, ref. forrige avsnitt, men som man kan oppnå ved innskuddsbasert pensjonsordning. Derfor er det ikke sikkert man trenger å være så misfornøyd med pensjonsordningen sin selv om man ikke har en garantert ytelse. Så kan man spørre seg hvorfor noen i det heletatt ønsker garanterte ordninger dersom de er så dårlige som jeg skriver. Det har nok en del med tapsaversjon å gjøre. Dersom vi er typen som sitter å se på pensjonskontoen vår hver måned og mister nattesøvnen når vi ser at vi har tapt penger fra én måned til den neste så vil kanskje en ytelsesbasert ordning være bedre for deg. Selv om det rent rasjonelt er dårligere, kan det gi mer optimal “nytte” for deg, ettersom du er villig til å gi avkall på potensiell ekstra avkastning i bytte mot tryggheten av en garantert ytelse. En annen årsak er nok at det er noe som henger igjen fra tidligere, hvor slike ordninger har vært “det vanlige” – og folk liker best å gjøre som alle andre…

Hvilken investeringsprofil bør du velge?

Når vi snakker om investeringsprofil kan vi enkelt si at vi mener; hvor stor prosentandel av pensjonspengene skal man plassere i aksjer (høy risiko) og hvor mye i obligasjoner (lav risiko).

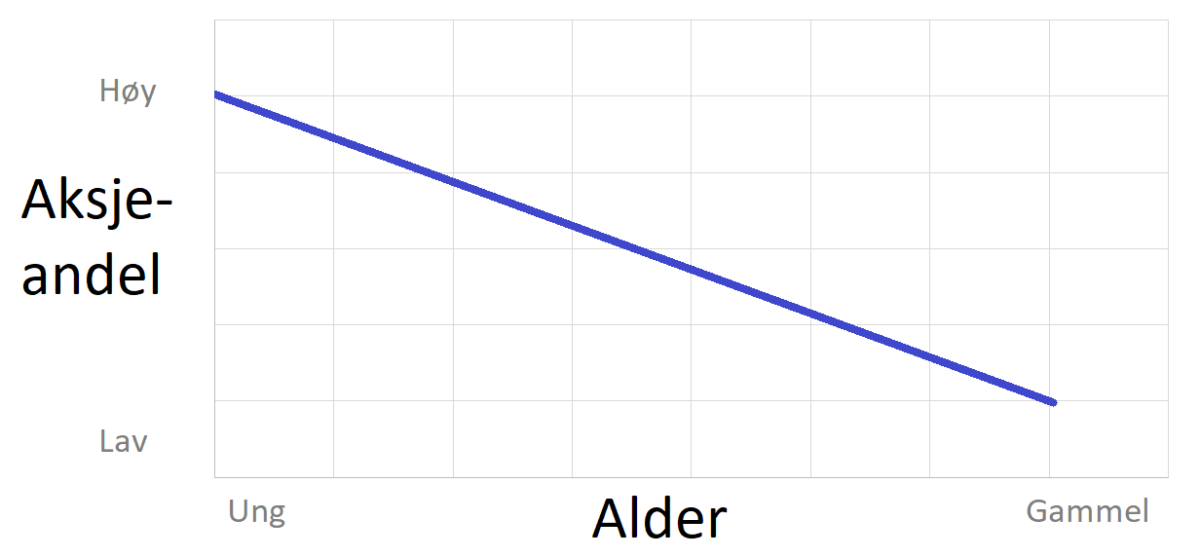
Det finnes ikke et fasitsvar – dette avhenger mye av din egen risikoappetitt. Er man ikke risikoavers bør man optimalt sett investere 100% av pensjonskapitalen i aksjer hele tiden, slik jeg beskrev i et tidligere avsnitt, men de fleste av oss har en viss grad av risikoaversjon. Et generelt råd når man skal velge aktiva-allokering, er å velge en høy aksjeandel (høy risiko) når du er ung, og gradvis trappe ned mens du beveger deg mot pensjonsalder. Noen forsikringsselskaper tilbyr løsninger som gjør dette automatisk for deg.

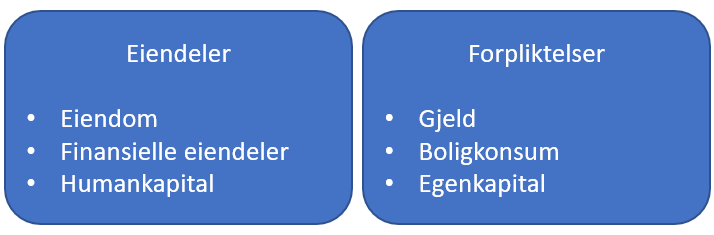
Det er ikke nødvendigvis så heldig å utsette pensjonen sin for høy risiko når det nærmer seg uttakstidspunkt, fordi da har du jo snart bruk for dem. Når du er ung er pengene for det første ikke like sårbare for svingninger, fordi eventuelle nedgangskonjunkturer vil med all sannsynlighet hentes inn av etterfølgende oppgangskonjunkturer. For det andre har du mye mer av din fremtidige inntekt liggende foran deg enn når du er gammel. De som leste innlegget om lån vil huske at jeg introduserte begrepet humankapital som en betegnelse for dagens verdi av din fremtidige inntekt. Ettersom humankapital anses som risikofritt, sier økonomisk teori at så lenge du er ung, kan det være optimalt å utsette mer av sine finansielle eiendeler for risiko når man er ung. For den som er spesielt interessert, og som ikke blir svimmel av tall, kan jeg forklare dette litt nærmere med et eksempel:

La oss anta at du har klart å gå inn i deg selv og finne din nyttefunksjon som gir deg en formel for din personlige optimale andel av risikofylte og risikofrie investeringer, og funnet ut at det som er optimalt for deg er 60% risikofritt og 40% i aksjer. Anta at du har 2,5 millioner kroner i finansiell formue (penger). La oss anta at du jobber i en trygg bedrift med fastlønn frem til du går av med pensjon, så du vet at verdien av all din fremtidige inntekt er 3 millioner. Da kan man kanskje tenke at man bør investere slik:

Aksjer: 40% = 1 million
Obligasjoner: 60% = 1,5 millioner

Det blir ikke riktig, fordi i tillegg til de 2,5 millionene du har i finansiell formue, har du også 3 millioner i humankapital. Totalt har du altså en “egenkapital” på 5,5 millioner, men bare 2,5 millioner av disse er penger du kan aktivt plassere. Resten er jo bundet opp i din framtidige inntekt, som vi altså anser som risikofritt. Dersom det er slik at du skal investere 60% risikofritt betyr det at du skal investere 60% av 5,5 millioner, altså 3,3 millioner risikofritt. Du har allerede 3 millioner plassert risikofritt i dag (din humankapital), så det betyr at du bør plassere 300.000 av din finansiell formue på 2,5 millioner i risikofrie instrumenter, og resten i aksjer. Da blir dine eiendeler fordelt slik:

Aksjer: 2,2 millioner
Obligasjoner: 300.000
(Humankapital: 3 millioner)

Så for å oppsummere; i teorien bør man ha en relativt stor andel av pensjonssparingen investert risikofylt når man er ung, og gradvis trappe ned når man blir eldre. (Dersom man ikke er risikoavers bør man ha pengene investert risikofylt hele livet.)

Hva gjør folk?

Sannheten er dessverre at folk ikke gjør noe. I hvertfall er det ikke mange nok som gjør nok. Folk flest tar dessverre ikke et aktivt valg, og ender derfor opp på den investeringsplanen som man får som standard. Dette er typisk 50% aksjeandel. Nesten halvparten av Norges pensjonssparing er investert med 50% aksjeandel… Mange lever nok i en tro om at pensjonen “ordner seg selv”, ved at folketrygden og det man har spart opp gjennom arbeidsgiver vil være bra nok til å leve komfortabelt som pensjonist. For de fleste er ikke dette sant.

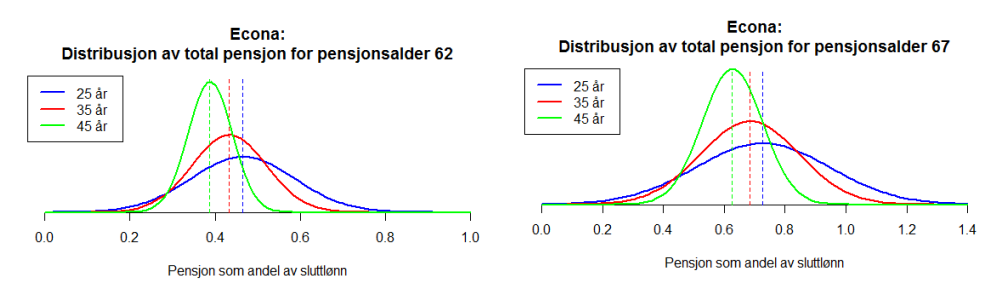
Det som er viktig å være obs på er at innskuddspensjon er relativt “nytt”, noe som betyr at det per i dag ikke finnes veldig store innskuddspensjonsformuer og derfor ikke veldig mye datagrunnlag å føre statistikk over. Det man imidlertid kan si med sikkerhet er at størrelsen på innskuddspensjonen vår vil være veldig viktig, og at avkastningen vi får på innskuddspensjonen vår vil kunne få store utslag for hvor mye vi vil få å rutte med som pensjonister. Så er det naturligvis slik at jo bedre innskuddspensjonsordning, jo større utslag vil avkastningen gi. Det vil med andre ord si at avkastningen vil ha større utslag på utbetalingene til en advokat enn en butikkmedarbeider.

Det disse figurene, hentet fra denne bacheloroppgaven, viser er blant annet at pensjonen til en person med innskuddspensjon vil variere veldig. Variasjonen drives i stor grad av avkastningen på innskuddspensjonen. Velger du en forsiktig profil, reduseres svingningene kraftig, men forventet pensjonsutbetaling i prosent av lønnen reduseres også kraftig. Med andre ord er mye av din pensjon avhengig av 1) din investeringsprofil og 2) utviklingen i aksjemarkedet. Det viser seg dessverre at alt for få nordmenn har forstått hvor mye dette har å si, og at særlig for oss som er unge i dag, så er dette virkeligheten vi må forholde oss til.

Hva skjer når jeg dør?

Hva som skjer med pensjonen din når du dør er forskjellig mellom ytelses- og innskuddspensjon. Dødelighetsarv er et konsept som bygger på at pensjonsmidler som tilhører en person som avgår ved døden går tilbake til ordningen, og fordeles blant de resterende kundene i ordningen. Konsekvensen av dødelighetsarv er at man har en slags forsikring i tilfelle man lever lengre, ved at man kan få utbetalt ytelsen selv om man skulle leve lengre enn det forventes at du skal. Til gjengjeld blir det ingenting til overs til etterlatte når du dør, dersom du skulle dø før forventet.

Ytelsespensjonen bygger altså på en forsikring som egentlig er motsatt av en livsforsikring. Ved en livsforsikring får man penger når man dør, mens ved en ytelsespensjon får man penger hvis man man lever lengre enn forventet, og ingenting når man dør før forventet – da går “overskuddet” tilbake i ordningen. Nå har du jo forsåvidt ikke noe bruk for penger når du er død heller, så jeg forstår at du sikkert tenker at det høres ut som en mye bedre deal for deg… Uansett; denne mekanismen finnes ikke i innskuddspensjon. Dersom man dør før man har fått hele innskuddspensjonen utbetalt, blir dette utbetalt til arvingene. Det vil ikke inngå i boet som sådan, men utbetales til den som i polisen er oppgitt som etterlatt. Dette kan føre til et dilemma: skal man ha en kort utbetalingsperiode og risikere å “gå tom”, eller ha en lang utbetalingsperiode og risikere å dø med en diger innskuddspensjon til de etterlatte? Dersom man velger en kort utbetalingsperiode, vil man etter kontoen er tom måtte leve på folketrygden som eneste løpende inntektskilde. Det kan være ganske kjipt hvis man skulle finne på å bli veldig gammel. I motsetning til hvordan pensjonssystemet var før, har man ingen forsikring som sikrer en en fast sum hele livet, så etter utbetalingsperioden for innskuddspensjonen har man ikke særlig igjen å leve for.

AFP – Avtalefestet pensjon

Privat AFP er ikke noe jeg går nøye innpå i dette innlegget. Avtalefestet pensjon er, i privat sektor, en tariffbasert pensjonsordning som ble innført i 1989 som et forsøk på å bøte på behovet enkelte yrkesgrupper (“sliterne” i arbeidslivet) hadde for en tidlig pensjonsordning. AFP-ytelsen er en livsvarig ytelse som kan tas ut fra fylte 62, så fremt man tilfredsstiller vilkårene for å motta AFP. I all hovedsak er det snakk om et påslag på pensjonsgivende inntekt frem til og med året man fyller 61. Det er en rekke vilkår – for eksempel skal du ha vært arbeidstaker i en bedrift som omfattes av AFP-ordningen i minst 7 av de siste 9 årene før du fyller 62 (med noen unntak for de født før 1955). Fra tid til annen er det artikler i avisene om folk som helt på tampen av karrieren havner i en uheldig situasjon som gjør at de mister retten til AFP, og derfor “taper” millionbeløp som de kunne fått fra denne ytelsen. Ordningen er et resultat av trepartssamarbeidet mellom arbeidsgiver- og arbeidstakerorganisasjonene og staten. Bedriftene som omfattes dekker omtrent 2/3 av utgiftene knyttet til denne ordningen og staten dekker resten.

AFP er en god ordning for de som har det, men det er lett å forstå at noen mener det er betenkelig at staten skal være med å finansiere 1/3 av en gullkantet ordning som bare noen få arbeidstakere har tilgang til. Storparten av arbeidsstyrken, inkludert mange lavtlønnede, har ikke tilgang til denne ordningen.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Da er vi kommet til den delen av pensjonssparingen som påvirkes aller mest av våre egne valg, og som for mange kanskje blir den mest krevende og uoversiktlige delen av pensjonssparingen. Den individuelle pensjonssparingen er delen av pensjonen vår som er helt og holdent opp til oss, og som derfor krever at vi er disiplinert. I følge en undersøkelse utført på vegne av DNB svarer bare 39% av norske kvinner og 50% av norske menn at de har noen form for pensjonssparing utover folketrygden og arbeidsgiverfinansierte ordninger.

Individuelle ordninger er ordninger mellom deg og leverandøren av spareproduktet du velger. Det vil si, staten har en viktig rolle også, som premissleverandør. Med det mener jeg at staten gir visse former for pensjonssparing skattemessige incentiver som ikke “vanlig sparing” har for å pushe folk til å binde en del av formuen sin i langsiktig pensjonssparing. Hvorfor gjør staten det? Jo, det er nok ganske enkelt fordi de vet at folk flest sparer alt for lite til pensjon, at folketrygden og arbeidsgiverfinansierte ordninger for de fleste ikke vil være nok, og at den beste måten å påvirke folks atferd på er ved å påvirke lommeboka deres.

Det finnes mange måter å spare til pensjon på når du skal spare på egenhånd. Mange velger å betale ned på boliglånet som en sparing, ettersom man da har sparepengene liggende som egenkapital i boligen. Skal du selge boligen og kjøpe deg noe billigere senere vil du kunne realisere noe av denne egenkapitalen. Skal du imidlertid flytte inn i en helt ny leilighet mer sentralt enn der du bor i dag, kan det hende at mye av sparepengene må gå med som egenkapital i ny bolig. Noen velger å kjøpe en hytte, som de tenker å selge når de blir pensjonister, men så finner de ut at det er dumt å selge hytta når de endelig har tid til å bruke den. Man bør altså ta høyde for flere eventualiteter, og da trenger man å ha flere produkter i verktøykassa.

Du kan alltids opprette en sparekonto, kalle den “pensjon” og sette over et beløp hver måned. Du kan også bare tenke at deler av fondssparingen din skal være øremerket pensjon. Mange banker har egne fond som er tiltenkt pensjonssparing. Dersom man er flink og disiplinert og ikke tar ut disse pengene før pensjonsalder, kan dette være en god løsning – iallfall for deler av pensjonssparingen. Å ha dette som sin eneste individuelle pensjonssparing er for mange en dårlig løsning, fordi slik sparing ikke forplikter nok, da det er mulig å ta ut sparepengene når som helst. For mange er det beste å putte deler av pensjonssparingen i en ordning hvor pengene blir låst frem til man når pensjonsalder. Jeg vil derfor fokusere denne delen av innlegget rundt det produktet som nok er best egnet for de fleste.

IPS – Individuell Pensjonssparing

Jeg vil legge hovedvekt på Individuell Pensjonssparing. IPS er en ordning som kom i 2017 og som tilbys av de fleste store pensjonsleverandørene. I følge Finans Norge er det omtrent 6 milliarder kroner investert i IPS, hvorav 60% av sparingen er gjort av menn, og 40% av kvinner. Konseptet er at man kan sette inn inntil 40.000 kroner per år i denne ordningen. Pengene man betaler inn i denne ordningen blir bundet til pensjonssparing frem til man er 62 år. Etter fylte 62 kan man velge å starte uttaket med én gang, eller vente til et senere tidspunkt. Midlene du har i IPS skal utbetales månedlig frem til du er 80 år. Det skal minimum utbetales over en periode på 10 år, som betyr at du senest kan starte uttaket det året du fyller 70. Starter du uttaket når du er 62 år, får du med andre ord en 18 års utbetalingstid. Dette skjønner vi at er en mindre fleksibel ordning enn å legge pensjonskapitalen på en sparekonto eller i vanlig fondssparing, hvor du kan ta ut så mye du vil, når du vil. Likevel vet vi jo at vi mennesker foretrekker konsum i dag foran konsum i morgen, så for de fleste vil det være behov for et produkt som disiplinerer oss ved mer jevn fordeling av pensjonssparingen, så vi ikke bruker opp alt med én gang, og må leve med svært lav inntekt de siste leveårene.

Derfor har altså staten gått inn for å gi skattemessige incentiver for IPS for å pushe oss til å spare langsiktig i et produkt som fordeler kapitalen vår jevnt over flere år. De viktigste skattemessige fordelene med IPS er:

1) Formuen du har spart opp som ligger innunder IPS er fritatt for formuesskatt. Det vil si at dersom du er i en netto formuesposisjon hvor du betaler formuesskatt, så vil det ikke beregnes formuesskatt av midlene du har innunder IPS-ordningen.

2) Innskuddet du gjør vil komme til fratrekk på alminnelig inntekt det året innskuddet gjøres. Det vil si at dersom du setter inn 40.000 kroner, vil alminnelig inntekt reduseres med 40.000. Dersom skatt på alminnelig inntekt er 22% betyr det at du sparer 8.800 i skatt det året. “Gratis penger” tenker du kanskje? Ja og nei. Den dagen du tar ut pengene igjen, vil de måtte skattes som alminnelig inntekt igjen. Likevel kan vi være ganske sikre på at 8.800 kroner i dag er verdt mer enn 8.800 kroner den dagen du blir 62, så sånn sett vil man sannsynligvis ha en økonomisk gunstig effektiv av å få utsatt skatten. De 8.800 kan du jo for eksempel sette inn på IPS neste år, eller i annen sparing. Skulle skattesatsen for alminnelig inntekt gå ned, vil du ha tjent litt ekstra, og skulle skattesatsen gå opp vil du måtte skatte mer i kroner og øre den dagen du tar det ut.

3) Avkastningen er fritatt for beskatning så lenge pengene står plassert i IPS. Det vil si at du kan omplassere pengene (for eksempel bytte fond) uten å måtte skatte av avkastningen så lenge man bytter innad i IPS-ordningen. Avkastningen skattes som alminnelig inntekt på samme måte som innskuddet, det året du tar det ut. En ting som kan være greit å være klar over er at ettersom avkastningen ikke skattes som kapitalinntekt, men som alminnelig inntekt, får man ingen glede av eventuelt opparbeidet skjermingsfradrag.

Det er spredning i prisene for IPS, så man bør ta en titt på prislistene før man setter i gang. Du vil for eksempel se at noen tilbydere (for eksempel Sparebank 1) tar et administrasjonsgebyr i tillegg til forvaltningsgebyr, mens andre ikke har dette administrasjonsgebyret. Utover forskjellen i pris på tvers av tilbyderne har du til en viss grad muligheten til å styre kostnadene litt selv. Jo høyere aksjeandel, jo høyere forvaltningsgebyr. Velger du et indeksfond eller investeringsprofil med lav aksjeandel vil du komme best ut kostnadsmessig, men på sikt vil du også få lavere avkastning. Det er også stor forskjell blant tilbyderne i fleksibiliteten man har for plasseringen av midlene. Hos noen leverandører har du valget mellom noen få alternativer basert på hvilken investeringsprofil du ønsker. Hos Sparebank 1 har du for eksempel 4 valg (25% aksjer, 50% aksjer, 75% aksjer og 100% aksjer). Hos DNB og Nordea kan du derimot velge mellom over 50 fond, med ulik grad av aksjeeksponering.

Egen Pensjonskonto (forventet januar 2021)

Fra 1. januar 2021 vil alle som har innskuddspensjon få “Egen Pensjonskonto”. Dette er besluttet av myndighetene, og er noe som skjer automatisk uten at du må foreta deg noe aktivt. Det som skjer er at du får en konto hvor all innskuddspensjon fra nåværende arbeidsgivere og gamle innskuddspensjoner (pensjonskapitalbevis) fra alle tidligere arbeidsgivere blir samlet. Pensjonskontoen vil bli opprettet hos den leverandøren du har innskuddspensjonen din hos i dag, altså den leverandøren din nåværende arbeidsgiver har avtale med. Det vil si at dersom du gjennom din arbeidsgiver har innskuddspensjonen din hos DNB i dag, vil pensjonskontoen din opprettes der. Følgelig vil alle pensjonskapitalbevis du har andre steder flyttes til DNB og slås sammen til én avtale den 1. april (med mindre du reserverer deg mot denne flyttingen innen 31. mars).

I dag dekker som tidligere nevnt arbeidsgiver kostnadene til forvaltningen av din innskuddspensjon, mens du selv betaler kostnadene knyttet til forvaltningen av tidligere innskuddspensjoner (pensjonskapitalbevis). Når Egen Pensjonskonto kommer, vil arbeidsgiveren din nå måtte dekke forvaltningskostnadene knyttet til dine pensjonskapitalbevis også. Dette forutsetter imidlertid at din pensjonskonto er hos arbeidsgivers leverandør.

Du står fritt til å flytte pensjonskontoen din. Hva betyr det i praksis? Jo, det betyr at du kan velge å samle pensjonen din hos en selvvalgt leverandør, altså en annen leverandør enn den som arbeidsgiveren din har avtale med. Noe man må huske da, er det jeg nettopp skrev om kostnader. Dersom du har pensjonskontoen din hos din arbeidsgivers pensjonsforvalter, betaler arbeidsgiver forvaltningskostnaden for din innskuddspensjon og pensjonskapitalbevis. Dersom du flytter pensjonskontoen din vekk fra leverandøren din arbeidsgiver har avtale med, er det plutselig du som må betale. Arbeidsgiver vil riktignok måtte betale en kompensasjon for dette, som skal gå med til å dekke kostnadene du får hos din selvvalgte leverandør. Ofte kan arbeidsgiveren din har forhandlet frem en avtale som er bedre enn den du må betale hvis du velger selvstendig leverandør, slik at du selv etter kompensasjonen kan tape på flyttingen.

For å oppsummere har du altså tre alternativer:

1) Samle innskuddspensjon og pensjonskapitalbevis i “Egen Pensjonskonto” hos din arbeidsgivers pensjonsforvalter (dette er det som vil skje automatisk hvis du ikke foretar deg noe)

2) Velge å ha din innskuddspensjon og dine pensjonskapitalbevis spredd blant flere leverandører.

3) Velge å samle innskuddspensjon og pensjonskapitalbevis hos en selvvalgt leverandør.

Personlig syns jeg Egen Pensjonskonto er veldig positivt. For det første er det normalt sett billigere og enklere å ha alt samlet på ett sted som én avtale fremfor å ha flere pensjonskapitalbevis liggende som individuelle avtaler. Mange som har hatt flere jobber oppigjennom har nok mange pensjonskapitalbevis liggende rundt hos ulike leverandører. For det andre vil det forhåpentligvis gjøre at flere tar et aktivt valg om hvordan de vil investere sine pensjonspenger. For det tredje gjør det at kunder nå har større og enklere valgfrihet rundt pensjonsforvaltningen sin, at leverandørene vil kjempe om kundene. Det kan føre til at prisene går ned, slik at hver enkelt får lavere kostnader knyttet til forvaltningen av pensjonssparingen, og derfor at man sitter igjen med mer pensjon for hver krone man sparer enn før.

Jeg håper dette innlegget har vært lærerikt, og enda viktigere håper jeg at innlegget har ført til at du har gått inn å sett på om pensjonen din har en investeringsprofil som er optimal for deg! Det vil alltids være noen som savner noe i et slikt innlegg, men jeg føler jeg har fått med det jeg ønsket å formidle.

Posted on 05.04.202019.04.2022

Kjapt om det norske skattesystemet

To ting er sikkert her i livet: døden og skatten.
– Benjamin Franklin

I disse dager melder skattemeldingen sin ankomst, og Altinn blir igjen overbelastet når alle skal inn samtidig. Det norske skattesystemet er så enkelt at folk flest

bruker bare noen få minutter på å se over skattemeldingen sin (selv om de fleste med fordel kanskje kunne viet den litt mer oppmerksomhet). I tillegg til å være et skattesystem som er veldig enkelt for (den private) skattebetaleren, er det også blant verdens mest effektive skattesystemer, og det eneste skattesystemet i verden som er designet av samfunnsøkokonomer ned til den minste detalj.

I dette innlegget skal jeg ikke gi noen veiledning til skattemeldingen. Jeg skal beskrive noen enkle grunnprinsipper bak skattesystemet, og jeg vil fokusere på personinntekt. Hensikten med innlegget er å belyse hvorfor skattesystemet vårt er slik det er, med enkle eksempler. Mange vil kanskje reagere på at jeg har utelatt mange skatteelementer som eiendsomsskatt, formuesskatt osv. Dette kommer jeg gjerne tilbake til i andre innlegg, men i den hensikt å få frem hovedtrekkene, virket det mest hensiktsmessig å holde detaljene til et minimum.

Laffer-kruven:

Denne kurven kalles Laffer-kurven (Laffer Curve). Vi ser at på venstre side av t* er den deriverte positiv, mens på den høyre siden er den deriverte negativ. På norsk betyr det at på venstresiden er inntekten til staten stigende ved økt skattetrykk, mens på høyre side er skatteinntekten synkende. For å illustrere dette med et eksempel, kan man se for seg bompenger. Dersom man øker avgiften, vil det komme et punkt (i dette tilfellet t*) hvor skatteinntektene (også kalt provenyet) vil begynne å falle, som følge av at folk slutter å kjøre bil. Dette er naturligvis ikke nødvendigvis noe negativt, da mye av hensikten med bomringene i utgangspunktet er å minske trafikken – ikke nødvendigvis å maksimere provenyet. Et annet og kanskje mer treffende eksempel er vanlig personbeskatning. Dersom skatt på inntekt blir for høy, vil man på et punkt enten slutte å jobbe (fordi inntekt etter skatt blir så lav at vi verdsetter fritiden vår mer enn ekstrainntekten), eller ved at andel svart arbeid øker. Med unntak av noen få tilfeller er det altså viktig for polikerne å sørge for at vi ikke havner på høyre side av t* i Laffer-kurven.

Effektivitetstapet:

Jeg vil illustrere en effekt ved skattlegging ved å se hva som skjer når vi legger en skatt per enhet solgt av en vare (slik som f.eks. mva). Figuren under viser det berømte markedskrysset. Det er det første man lærer når man tar et kurs i samfunnsøkonomi. Du kan se for deg at det viser samlet etterspørsel for en vare, representert ved den synkende etterspørselskurven, og det samlede tilbudet for en vare, representert ved den stigende tilbudskurven. Etterspørselskurven viser konsumentenes betalingsvillighet for produktet, mens tilbudskurven viser bedriftens marginalkostnad. Marginalkostnad er den kostnaden bedriften har ved å produsere én ekstra enhet av produktet. Denne antas i de fleste normaltilfeller å være stigende.

I et “perfekt marked” (med blant annet fullkommen konkurranse) vil prisen på produktet være P0, og det perfekte kvantum vil være K0. Dette er det punktet som gjør at det tilbys like mange varer som det etterspørres (K0), og hvor det såkalt samfunnsmessige overskuddet maksimeres. På dette punktet får alle som ønsker å kjøpe produktet for mer enn kostnaden av å produsere det, kjøpt varen. Vi ser at hele det avgrensede arealet innenfor tilbuds- og etterspørselskurven er skravert. Arealet som er skravert med rødt kalles “konsumentoverskuddet”. Konsumentoverskuddet kommer av at det finnes konsumenter som er villige til å betale mer enn P0 for varen. De som ligger lengst til venstre (høyest opp) i etterspørselskurven har det høyeste konsumentoverskuddet, mens “den siste konsumenteten”, som er villig til å betale bare P0 for varen ikke har noe konsumentoverskudd. Arealet som er skravert med blått kalles produsentoverskuddet, og skyldes at bedriftens gjennomsnittlige marginalkostnad på produktet blir lavere enn salgspris P0.

Vi legger nå på en skatt for produktet. Som vi ser fører dette til økt pris og redusert etterspørsel. Prisen ut til konsumenten er Pk, mens bedriften sitter igjen med Pp. Til pris Pk er det færre som har betalingsvillighet for produktet, og tilpasningen i markedet skjer derfor på et lavere kvantum. Du kan se at det er veldig mange flere konsumenter som er villig til å kjøpe produktet til Pp kroner, men siden utsalgsprisen er Pk, er det bare Kt som vil kjøpe produktet. Vi ser at skatten absorberer både deler av konsumentoverskuddet og produsentoverskuddet, slik at staten får inn A+B i inntekt. Det er fremdeles noe overskudd for konsument og produsent, men poenget er at summen av A + B + rød + blå nå er lavere enn summen av rød + blå før skatten. Det er nemlig to områder til, C + D, som ikke kommer verken stat, konsument eller produsent til gode. Summen av total velferd var altså større før skatten ble innført. Dette velferdstapet kalles effektivitetstapet. Vi kan se for oss et lignende fenomen med arbeidsinntekt, hvor arbeidstakerens tilbud av arbeidstimer representeres av tilbudskurven, og arbeidsgivers etterspørsel representeres ved etterspørselskurven. Vi ser at jo høyere skatt på inntekt, jo færre arbeidstimer tilbys i markedet.

Okey, så skatt fører til et effektivitetstap i markedet, selv om vi selvfølgelig vet at det er nødvendig for å finansiere politi, helsevesen, pensjoner og infrastruktur. Et viktig tiltak er derfor å forsøke å minimere dette effektivitetstapet. Derfor er det viktig å være klar over følgende: dobler vi skattesatsen, så mer enn dobler effektivitetstapet seg. Dere får unnskylde at jeg ikke er så flink til å tegne som jeg er til mye annet, men i figuren under har jeg forsøkt å legge på en skatt som er så å si dobbelt å stor som den vi har i forrige figur. Vi kan se at områdene med C og D har mer enn doblet seg, som betyr at velferdstapet er mer enn doblet ved å doble skattesatsen.

Hvorfor har jeg brukt så mye tid på å tegne dette i paint? Er det viktig? Ja – det er faktisk veldig sentralt for å forstå skattesystemet vårt. Dette fenomenet er nemlig årsaken til vi har lave skattesatser, men heller skattlegger på et bredt skattegrunnlag. Dette er årsaken til at staten ikke henter inn alle sine skatteinntekter gjennom ett skattegrunnlag (f.eks. inntektsskatt) – fordi effektivitetstapet ville vært enormt høyt. Jean Baptiste Colbert (finansminsteren til Louis XIV) sammenlignet skattlegging med å plukke fjær av en gås; det handler om å plukke fjæra på en slik måte at gåsa merker minst mulig. Jo flere aktiviteter vi skattelegger, desto lavere skatt per aktivitet – og desto mindre merker folk at de skattlegges.

En naturlig konsekvens av dette er at dersom vi skal redusere skatten i ett marked, må det økes i et annet marked dersom skatteinntektene skal opprettholdes. Da vil, som vi har sett over, velferdstapet i samfunnet bli høyere totalt sett som følge av overproporsjonale effektivitetstap.

Det betyr også at det er mer gunstig å ha høye skattesatser i markeder hvor tilbud og etterspørsel ikke påvirkes like mye av pris, og derfor ikke påvirkes mye av skatt. Eksempler på dette er markeder hvor etterspørselskurven er mer eller mindre vertikal, som betyr at kvantumet som selges er mer eller mindre uavhengig av pris (typisk nødvendighetsvarer, slik som medisiner). På økonomispråket kaller vi dette uelastisk etterspørsel.

Tenk over følgende utsagn:
– “Det er bedre å fjerne NRK-avgiften, og heller øke inntektsskatten litt.”
– “Vi bør fjerne selskapsskatten, og heller hente inn skatteinntektene gjennom å øke andre skatter.”
– “Det er urimelig at vi skal skatte av samme skattegrunnlag flere ganger, ved at vi først skatter av arbeidsinntekt, deretter betaler moms når vi handler for den allerede skattlagte inntekten.”

Jeg skal ikke si at det er noen fasit, fordi det vil alltid kunne være noen som ville kommet bedre ut ved at man justerte på skattesatsene i enkelte markeder (og noen vil komme verre ut). Det jeg som økonom kan si, og som du som leser nå vet, er imidlertid at dersom vi skal se på nasjonen som helhet så er utsagenene feil. Totalt sett ville vi kommet dårligere ut dersom vi ikke hadde fordelt skattene slik vi gjør i dag.

Brede skattegrunnlag, lave skattesatser og skattemessig likebehandling av næringer, virksomheter og investeringer vil bidra til at ressursene utnyttes best mulig.
– Regjeringens skatte- og avgiftspolitikk (Nasjonalbudsjettet 2019)

Skattearbitrasje:

Arbitrasje betyr å utnytte prisforskjeller på samme vare eller verdipapir i forskjellige markeder. I praksis betyr det altså “gratis penger”, ved at man får en avkastning uten noen risiko. En investor vil alltid ønske å investere der avkastning etter skatt er høyest mulig. Skattearbitrasje kan oppstå dersom det er mulig å utnytte satsforskjeller i skattesystemet. Vi kan illustrere dette på en enkel måte, ved å se for oss at vi har to skattesatser:
– En skattesats på lønnsinntekt: T1
– En skattesats på bedriftsinntekt: T2
– Vi ser for oss at det ikke er noen skatt på utbytte
– Vi antar at T1 er større enn T2

Det er lett å se av eksemplet over at det vil være mulig å utnytte dette. I et slikt system vil man for eksempel kunne utnytte satsforskjellene ved at man opprettet seg en bedrift og fakturerte arbeidstimene sine, heller enn å motta lønn. Da kunne man tatt ut pengene fra bedriften i form av utbytte, og altså bare betalt bedriftsskatt (T2). Resultatet ville vært at man betalte mindre skatt, ved at man hadde tilpasset seg på en viss måte i skattesystemet. Ville du tatt ut pengene fra selskapet ditt som lønn, dersom skattesatsen på lønnsinntekt var høyere enn utbytteskatt?

Svaret på spørsmålet over er nei, og vi vet av erfaring at man tilpasser seg der det er mulig. Jeg skal fortelle en liten historie. Etter skattereformen i 1992, og frem til 2006 var det ikke noe skatt på utbytte. Dersom du eide mer enn 2/3 av aksjene i en bedrift ble du beskattet som “aktiv eier”. Basert på bedirftens kapital, og et mål på avkastning, ble det beregnet en kapitalinntekt for eieren. Deretter ble det beregnet en arbeidsinntekt basert på overskudd minus kapitalinntekten. For eksempel dersom kapitalen i bedriften var 200.000, og målet på avkastningen var 7%, ble det beregnet kapitalinntekt lik 200.000*7% = 14.000. Dersom overskuddet var 100.000, ble den aktive eierens arbeidsinntekt beregnet til 100.000-14.000 = 86.000. Denne lønnsinntekten ble deretter skattet av som normalt. Jeg sa at dette gjaldt dersom man eide mer enn 2/3 av bedriften. Vel, det som skjedde var at det etterhvert ikke eksisterte et eneste aksjeselskap her i landet hvor noen eide mer enn 2/3 av aksjene. Dersom man gjorde det, “solgte” (les: overførte) man aksjer til venner og bekjente, for å unngå å bli beskattet som “aktiv eier”, og heller komme innunder betegnelsen “passiv investor”. Med andre ord betalte en “passiv investor” som tok ut utbytte kun bedriftsskatt (på den tiden 28%), mens lønnsmottakere skattet mye mer (på den tiden var marginalskatt på lønn like under 50%)

Vi ser at slike arbitrasjemuligheter vil kunne elimineres dersom man har et skattesystem hvor forskjellen på marginalskattesatsen på personinntekt og eierinntekt (inkludert bedriftsskatt) er tilnærmet lik null. Dette er slik det norske skattesystemet er designet. For de spesielt interesserte skal jeg forklare dette nærmere senere.

En ting veldig mange ikke ser ut til å forstå er nettopp dette. Hvis du tukler med én av skattesatsene så påvirkes hele skattesystemet. I det øyeblikket vi øker trinnskatten på lønn må vi også øke utbytteskatten. Hvorfor? Fordi vi ikke skal skape incentiver til inntektsskifting eller skattearbitrasje. Vi ønsker ikke at folk i skattesystemet skal kunne foreta arbitrasjetransaksjoner uten å ta risiko bare ved å posisjonere seg innenfor skattesystemet (eksempelvis velge hvilken institusjonell posisjon man tar – lønnsmottaker, bedrift etc.)

Omfordelingseffekter

Før jeg skriver om omfordelingseffektene ved skattesystemet, må jeg forklare begrepet jeg nettopp brukte: marginalskatt. Den effektive marginalskatten tilsvarer den prosenten du må betale i skatt på din neste inntjente krone. Den defineres som:

Det er den effektive skattesatsen som avgjør skattesystemets fordelingsegenskaper. Den effektive skattesatsen er egentlig det samme som en gjennomssnittsskatt, og defineres slik:

, vi ser at det som ligger over brøkstreken er den faktisk betalte skatten. Faktiske inntekter kan avvike fra skattegrunnlag (vi har minstefradrag, rentefradrag osv som gjør skattegrunnlaget lavere enn faktiske inntekter). Bare dersom skattegrunnlaget er lik faktisk inntekt vil effektiv skattesats være lik formell skattesats, og da har vi et flatt skattesystem. Da er gjennomsnittsskatten og skattesatsen helt lik.

Vi kan tenke oss: vi har betalt 100.000 i skatt i år, vi hadde 1.000.000 i inntekt. Da er gjennomsnittsskatten 100/1000 = 10%. Hvis jeg nå tjente 3.000.000, og betalte 150.000 i skatt ville gjennomsnittsskatten gå ned til 5%. Det betyr at jo rikere vi er, jo mindre andel av bruttoinntekten betaler vi i skatt. Dette er et regressivt skattesystem. Det fordeler fra fattige til rike. La oss si at skatteøkningen heller økte til 350.000 ved en bruttolønn på 2.000.000. Da ville jeg betalt mer i skatt som andel av bruttoinntekt. Da har vi et progressivt skattesystem som fordeler fra rik til fattig. Den observante vil se at det samme gjelder for marginalskatten; dersom marginalskatten er økende med stigende inntekt, vil skattesystemet være progressivt.

Et progressivt skattesystem fører altså til at de med høy inntekt betaler en større andel av inntekten sin i skatt enn de med lav inntekt. Dette kalles evneprinsippet, og det norske skattesystemet er tuftet på dette prinsippet. Mange mener at dette er urettferdig. Jeg skal forholde meg politisk uavhengig i denne sammenheng, men det kan til en viss grad forsvares rent samfunnsøkonomisk også, og jeg skal illustrere det med et enkelt eksempel:
– Person A tjener 400.000 i året før skatt
– Person B tjener 4.000.000 i året før skatt
– Staten må få inn 200.000 kroner i skatteinntekter, og har to muligheter:
1. Begge skatter 100.000 hver
2. Person A skatter 50.000, og person B skatter 150.000.

Hva tror du vil skape mest verdiskapning i samfunnet? Med all sannsynlighet vil alternativ 2 skape mest verdi, og jeg skal forklare hvorfor. I økonomisk teori sier vi at man har avtakende grensenytte når det gjelder konsum, som ganske enkelt betyr at selv om vi opplever økt nytte (glede/tilfredshet) ved økt konsum, så avtar nytten jo mer vi konsumerer. Avtakende grensenytte betyr også at du har mer glede av en krone ekstra jo mindre penger du har. Det er stor sannsynlighet for person A vil bruke mer av de 50.000 ekstra h*n får i disponibel inntekt til å kjøpe varer og tjenester enn det person B ville gjort. Isolert sett er det bedre for samfunnets verdiskaping at pengene brukes til kjøp av varer og tjenester enn at de går med til å øke en persons formue.

Et annet virkemiddel vi bruker i skattesystemet er bunnfradrag. Bunnfrardaget gjør at gjennomssnittskatten på en lavtlønnet person er lavere enn en høytlønnet. Jo høyere bunnfradrag, jo mer omfordeling. Vi kan se på et enkelt eksempel igjen:

Skattesats: 22%
Bunnfrardrag: 86.000

Person A	Person B
Inntekt: 400.000	Inntekt: 700.000
Skattbar inntekt = 400.000 – 86.000 = 314.000	Skattbar inntekt = 700.000 – 86.000 = 614.000
Gjennomsnittskatt = (314.000*0,22)/400.000 = 17,27%	Gjennomsnittskatt = (614.000*0,22)/700.000 = 19,30%

Legg merke til:
– Lavere gjennomsnittskatt for person A (lavest lønn) enn person B.
– Dersom det ikke fantes et bunnfradrag ville begge hatt samme gjennomssnittskatt (22%).
– Marginalskatten, altså den skattesatsen vi betaler på siste krone (22%) er høyere enn gjennomssnittskatten.

Alminnelig skattesats, trygdeavgift og trinnskatt

Skattesatsene kan være ulike fra år til år. I løpet av de siste årene har skattesatsen på alminnelig inntekt og selskapsskatten blitt nedjustert flere ganger, noe som først og fremst er veldig irriterende for sånne som meg, som lager eksempeloppgaver for studenter, og dermed må endre både oppgaver og løsningsforslag ofte. Nok om det…

Den alminnelige skattesatsen ilegges den alminnelige inntekten. Hva ligger i begrepet alminnelig inntekt? Alminnelig inntekt er selve ryggraden i det norske skattesystemet. Når vi begynner å motta lønn “starter” vi på alminnelig inntektsskatt. Det er også det bedriften betaler (med samme sats som lønnsmottakere), og vi betaler alminnelig inntektsskatt på renteinntekt. Hos bedriftene er skattesatsen flat (fast 22%), mens vi lønnstakere betaler trinnskatt, som blir høyere jo mer inntekt vi får. Trinnskatt er en skatt man betaler på den inntekt som ligger innenfor de respektive intervallene. Jeg skal illustrere med et eksempel senere. Ved beregning av alminnelig inntekt finnes det to fradrag vi må kjenne til: minstefradraget og personfradraget. Minstefradraget er et standardfradrag som automatisk trekkes fra lønn, pensjon og lignende inntekt. For de fleste vil det ikke være aktuelt å endre på denne, da det beregnes automatisk når du endrer på lønnsinntekten din i skattemeldingen. For noen kan det likevel være aktuelt å endre på denne dersom man for eksempel har faktiske kostnader knyttet til jobb som er høyere enn minstefradraget. I så tilfelle kan man kreve fradrag for disse i skattemeldingen. Minstefradraget beregnes med grunnlag av en sats på 45% av lønnsinntekt, med en nedre grense på 31.800 kroner og en øvre grense på 104.450 kroner. Personfradraget er et generelt bunnfradrag som i 2020 er 51.300 kroner.

Den høyeste marginalskatten på lønnsinntekt er 46,4%. Jeg skal vise hvordan vi kommer frem til det:

Skattesatser 2020
Skatt på alminnelig inntekt = 22%
Trinnskatt 1 (180.800-254.500) = 1,9%
Trinnskatt 2 (254.500-639.750) = 4,2%
Trinnskatt 3 (639.750-999.550) = 13,2%
Trinnskatt 4 (over 999.550) = 16,2%
Trygdeavgift = 8,2%

Vi ser at den høyeste marginalskatten vi får er 22+16,2+8,2 = 46,4%. Dette gjelder for inntekt over 999.550. Dersom man tjener 500.000 er marginalskatten 22+4,2+8,2 = 34,4%, fordi det da er trinnskatt 2 som slår inn.

La oss regne på et eksempel, hvor vi tar utgangspunkt i en person som tjener 500.000. La oss se hva samlet inntektsskatt blir for denne personen, og hva gjennomssnittskatten blir. Først beregner vi den alminnelige inntekten, deretter skatten. For eksemplets skyld ser vi bort fra eventuelle andre fradrag, som for eksempel fradrag for gjeldsrenter osv. Dette er kun for å forstå grunnelementene.

Alminnelig inntekt:

Lønnsinntekt	500.000
– Minstefradrag	104.450 (500.000*0,45 = 225.000, men øvre grense er 104.450)
– Personfradrag	51.300
= Skattegrunnlag alminnelig inntekt	344.250

Skattesats	Skatt å betale	Beregning
Skatt på alminnelig inntekt (22%)	75.735	344.250*0,22
Trinnskatt 1 (1,9%)	1.400	(254.500 – 180.800)*0,019
Trinnskatt 2 (4,2%)	10.311	(500.000-254.500)*0,042
Trygdeavgift (8,2%)	41.000	500.000*0,082
Samlet inntektsskatt	128.086	75.375+1.400+10.311+41.000

Denne personens gjennomssnittskatt var 128.086/500.000 = 25,6 %, mens marginalskatten var 34,4%. Det betyr at dersom personen tjente 100 kroner til, ville han betalt 34,4% skatt på denne hundrelappen.

Legg merke til:
– Du betaler bare trinnskatt for den delen av inntekten som havner innenfor intervallet, og ikke for hele inntekten som ligger over innslagspunktet (med unntak av trinnskatt 4, som ikke har noe øvre grense)
– Minstefradrag og personfradrag vil ha størst effekt på gjennomsnittskatten til personer med lav inntekt.
– Personer med inntekt over 232.111 vil oppnå øvre grense på minstefradraget.

Eierinntekt vs lønnsinntekt

Vi har tidligere sett at høyeste marginalskatt for lønnsinntekt er 46,4%, men hva blir marginalskatten for eierinntekt?

Dersom vi i stedet for å motta lønnsinntekt hadde opprettet en bedrift og tjent alle pengene våre i bedriften, ville vi først skattet 22% av bedriftens inntekter (husk at selskapsskatten er lik alminnelig skattesats, for tiden 22%). Så husker vi at kapitalinntekter beskattes med alminnelig skattesats, så da skulle man tro at når man tok ut utbytte fra denne bedriften, skal man skatte 22% av utbyttet. Når du tar ut utbytte, beskattes du imidlertid med 22% multiplisert med en oppjusteringsfaktor, for tiden 1,44. Det vil si at når du tar ut utbytte, beskattes du med 22%*1,44=31,68%.

Da blir regnestykket slik:

Da kan vi se at effektiv skattesats blir 0,22 + (1-0,22)*0,22*1,44 = 46,7%, som er ganske likt 46,4% som er effektiv skattesats på marginen for lønnsinntekt. Her ser vi altså igjen at skattesystemet er konstruert slik at det skal være nøytralitet knyttet til om vi tjener penger som lønn eller om vi tar det ut som utbytte fra AS. Hvorfor har vi en slik oppjusteringsfaktor? Vel, det kan være av praktiske årsaker, men det kan like gjerne være at politikerne ikke ønsker å fortelle oss i klartekst hva eierskatten er. Det blir kanskje mindre spetakkel fra gåsa dersom de øker en justeringsfaktor som kanskje de færreste vet eksisterer enn om de øker skattesatsen.

Dersom vi ikke hadde hatt oppjusteringsfaktoren kan vi se at effekitv skattesats ville blitt 0,22 + (1-0,22)*0,22 = 39,16%. Dette er lavere enn marginalskatt på lønnsinntekt, hvilket ville generert et incentiv til å skifte inntekt fra lønnsinntekt til eierinntekt. For å motvirke dette incentivet har man derfor en justeringsfaktor.

I 2006 ble det i Norge innført en aksjonærmodell. Aksjonærmodellen sier at aksjeinntekter (enten det er utbytte eller gevinst) skattes som alminnelig inntekt for det beløp som overstiger et skjermingsfradrag. Jeg har skrevet om skjermingsfradrag i et eget innlegg, så jeg skal ikke beskrive dette nærmere i dette innlegget.

Et annet viktig prisnipp er fritaksmetoden, som sier at aksjeselskaper er fritatt for skatt på aksjeinntekter, aksjeutbytte og aksjegevinster. Fritaksmetodens formål er å unngå såkalt kjedebeskatning, altså at slike inntekter blir beskattet flere ganger i én og samme eierkjede. Dette unngår man ved at slik inntekt ikke beskattes før den dagen de taes ut av selskapet. Når inntekten tas ut av selskapet, beskattes eieren med eierskatt for den delen av utbyttet som overstiger skjermingsfradraget.

Dette var veldig grunnleggende, men det var alt jeg tenkte å skrive om i dette innlegget. Er det noe innenfor tema skatt du ønsker jeg skal gå mer i dybden på?

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Posted on 24.03.202006.04.2020

Hva betyr den midlertidige endringen i boliglånsforskriften?

Slik dere kunne lese i mitt innlegg om lån er bankenes utlånspraksis begrenset av en rekke reguleringer. Mest kjent for de fleste er boliglånsforskriften, eller “Forskrift om krav til nye utlån med pant i bolig” som den heter.

Dette er en forskrift som er kommet først og fremst på grunn av den økende gjeldsbelastningen blant norske husholdninger. Kort oppsummert sier den dette:

For Oslo	For resten av landet
Lånekundens samlede gjeld skal ikke overstige fem ganger bruttoinntekt (inkl forbrukslån, studielån osv.)	Lånekundens samlede gjeld skal ikke overstige fem ganger bruttoinntekt (inkl forbrukslån, studielån osv.)
Det skal kreves minst 40% egenkapital ved kjøp av sekundærbolig (bolig nr 2, 3 osv)
Det skal kreves 15% egenkapital ved kjøp av primærbolig.	Det skal kreves 15% egenkapital ved kjøp av primærbolig.
Avdrag kreves for lån som overstiger 60% av boligens verdi.	Avdrag kreves for lån som overstiger 60% av boligens verdi.
Rammelån kan ikke gis når lånerammen overstiger 60% av boligens verdi.	Rammelån kan ikke gis når lånerammen overstiger 60% av boligens verdi.

Banken kan gjøre unntak utenfor kravene, men bare for 10% av bankens totale innvilgede lån (8% i Oslo).

I går, 23. mars 2020, vedtok Finansdepartementet en midlertidig endring i boliglånsforskriften, i all hovedsak for å øke fleksibiliteten for bankene slik at de skal være i bedre stand til å hjelpe kundene sine gjennom de økonomiske utfordringene koronaviruset medfører. Endringen de har gjort er å øke fleksibilitetskvotene som står med uthevet skrift under tabellen over. I stedet for henholdsvis 8% i Oslo og 10% i resten av landet, er nå kvotene økt til 20% for hele landet (inkludert Oslo).

Både boliglånsforskriften, og den ikke like kjente forbrukslånsforskriften har et såkalt “avdragskrav”, som betyr at det stilles krav til at både boliglån og forbrukslån må nedbetales etter en fastsatt nedbetalingsplan. Som dere er kjent med er det imidlertid et unntak for dette i boliglånsforskriften, som gjelder lån med sikkerhet i bolig hvor belåningsgraden er under 60%.

Departementet skriver at:

Begge forskriftene åpner for at bankene kan innvilge midlertidig avdragsfrihet på grunn av omstendigheter som inntrer i lånets løpetid, og som midlertidig forverrer kundens betalingsevne. Hvis bankene i dagens situasjon gir midlertidig utsettelse av betaling av renter og avdrag på et eksisterende lån, skal det derfor ikke regnes som et nytt lån etter forskriftene. Det kan innvilges avdrags- og renteutsettelse i inntil seks måneder.

Hva betyr dette i praksis? Dette betyr at alle kunder med løpende (eksisterende) bolig- eller forbrukslån i banken kan få innvilget avdragsfrihet (at man betaler kun renter) og/eller betalingsutsettelse (på både rente og avdrag) i inntil 6 måneder, uten at banken behøver å melde inn dette som en del av bruddkvota (fleksibilitetskvota). Dette gjør videre at bankene kan bruke fleksibilitetskvota på nye lån eller ved refiansiering av lån.

Hvorfor er dette så bra?

At løpende lån kan holdes utenfor bruddkvota betyr for det første at banken kan gi avdragsfrihet/betalingsutsettelse til mer eller mindre alle som trenger det, ikke bare 20% av lånevolumet. Det betyr videre at banken kan benytte fleksibilitetskvota til å imøtekomme kunder som trenger å opprette nye lån, men som har behov for fleksibiliteten med avdragsfrihet fra starten av låneperioden. Dette er gode nyheter for for eksempel bedriftseiere som stiller sine private boliger som sikkerhet for lån til bedriften, som nå har muligheten til å refinansiere sine lån for å hjelpe bedriften gjennom krisen.

Den midlertidige endringen skal i utgangspunktet gjelde 2. kvartal 2020, men kan bli forlenget.

Finansministeren undersktreker at tiltaket ikke kommer for å stimulere aktiviteten i bolig- og kredittmarkedet, men for å gi bankene rom til å utøve godt bankhåndtverk. Aner jeg en liten anerkjennelse fra ministeren her, om at den originale forskriften har begrenset bankenes evne til å utøve godt bankhåndtverk?

Posted on 04.03.201910.06.2023

Bedriftsøkonomi og finans – arbeidskrav 8 (2019)

Her kommer veiledning til siste arbeidskrav i bedriftsøkonomi og finans dette semesteret!

Spørsmål 1

Du setter kr 40 000 i banken. Innskuddsrenten er 2,2 % per år. Hva har beløpet vokst til etter fem år? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

På finanskalkulator (jeg bruker Texas Instruments sin)

PV: -40.000 (husk minus)
N: 5
I/Y: 2,2
CPT–>FV = ?

Spørsmål 2

Hvor mye penger må du sette i banken i dag for at innskuddet skal vokse til kr 50 000 om fem år? Bruk en rentesats på 2,1 % per år. Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

Kalkulator:

FV: -50000
N: 5
I/Y: 2,1
CPT–>PV = ?

Spørsmål 3

Du tar opp et kortsiktig annuitetslån på kr 60 000. Lånet skal tilbakebetales over to år med like store terminbeløp ved utgangen av hvert kvartal. Lånerenten er 8% per år. Vi ser bort fra andre lånekostnader. Hva er terminbeløpet (=sum renter og avdrag)? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

Bruk finanskalkulator f.eks.

PV: -60000
N: 8
I/Y: 2
CPT–>PMT

Svaret du får (PMT) er terminbeløpet

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077

Spørsmål 4

En elektrokjede tilbyr deg “gratis” kreditt i tre måneder. Elektrokjeden oppgir at du kun må betale et gebyr på kr 200 ved kjøp av en vare, men ingen renter, hvis det beløpet du skylder, blir betalt senest etter tre måneder. Anta at du kjøper en vare for kr 4 000, betaler gebyret på kr 200, utsetter betalingen av varen, for så å betale kr 4 000 etter tre måneder. Hva blir den effektive renten per år for denne kreditten? Oppgi svaret (kun tallet) i % med to desimalers nøyaktighet.

Du må sette opp de to alternativene og la de danne en differansekontantstrøm

	I dag	Om en måned	Om to måneder	Om tre måneder
Kontant	-4000	0	0	0
Kreditt	-200	0	0	-4000
Differansekontantstrøm	*3800(1)**	0	0	-4000
Effektiv rente (IRR)(2)*	?%
Effektiv årsrente(*3)	?%

*1 (-200) – (-4000) = 3800
*2: Legg inn kontantstrømmen i kalkulator og finn internrenta. IRR er da effektiv månedsrente.
*3: F.eks. hvis månedsrenta er 2,63%, omregner vi til årsrente slik: (1+0,00263)¹² – 1 = 36,59%. Gjør det med de tallene du får

EDIT:
Eventuelt kan du gjøre det sånn:

	T0 (i dag)	T1 (3mnd)
Kontant	4000	0
Utsettelse	-200	-4000
Differansekontantstrøm	3800	-4000
IRR (effektiv rente) pr 3mnd	??
IRR årlig (fra kort til lang rente)	?? *(1)

*(1): (1+r)^t – 1 ==> [(1,?)^4] -1
eks: hvis du finner ut at IRR per tre måneder er 1,7%, regner du ut det sånn: (1+0,017)^4 – 1 = 0,0697537 = 6,98%

Her er tanken den at du regner ut IRR (det vil si effektiv rent) for hvert kvartal (tre mnd). Det vil med andre ord si at heller enn å opphøye i 12, som du gjør når du har månedsrenta, opphøyer du i 4, fordi det er 4 kvartaler i et år. Det er litt mindre trykking, men fremgangsmåten er jo den samme.

Et fem-årig investeringsprosjekt forventes å ha følgende kontantstrøm i mill. kroner: ( -10, 3, 4, 5, 4,3). Avkastningskravet er 20% per år. Hva er prosjektets nåverdi? Oppgi svaret i millioner kroner med to desimalers nøyaktighet.Spørsmål 5

Legg inn kontantstrømmen i kalkulatoren din, legg inn avkastningskravet = 20% og la kalkulatoren kalkulere nåverdien. Hvis du ikke vet hvordan du regner ut nåverdi på kalkulatoren må du lære deg det. Spander en white russian på en venn, og få han eller henne til å lære deg det.

Spørsmål 6

Et fem-årig investeringsprosjekt forventes å ha følgende kontantstrøm i mill. kroner: ( -10, 3, 4, 5, 4,3). Avkastningskravet er 20% per år. Hva er prosjektets internrente? Oppgi svaret (kun tallet) i % med to desimalers nøyaktighet.

Et par tastetrykk til så har du regnet ut IRR. Hvis du ikke vet hvordan du regner ut IRR på kalkulatoren må du lære deg det. Spander en white russian på en venn, og få han eller henne til å lære deg det.

For den interesserte:

Hva betyr det egentlig at et prosjekt har positiv nåverdi? Betyr det at hvis nåverdien er 100 millioner, så er avkastningen på prosjektet 100 millioner? Nei, det gjør det ikke. Det betyr at prosjektets avkastning er 100 millioner kroner MER enn det vi alternativt kunne fått ved å investere pengene våres annerledes. Jeg pleier å si at verdiskapning handler om hva vi måler i forhold til. Hva kunne vi alternativt fått ut av ressursene? Noen ganger kan vi jo måle opp mot nåsituasjonen, men uansett: det handler om alternativ anvendelse av kapital. Det jeg prøver å formidle her er at verdiskapning skjer når et prosjekt skaper verdier utover beste alternative anvendelse av ressurser. Det er DETTE som skaper positiv nåverdi.

Begrepet “positiv nåverdi” har mange flere navn: superprofitt, EVA (Economic Value Added), Residualinntekt, økonomisk rente osv.

Verdiskapningen skjer altså når man tar ut en fortjeneste som er unormalt høy. Det skal i teorien ikke være mulig å gjøre i et effisient marked, ettersom det alltid vil komme nye aktører i markeder der det er mulig å oppnå superprofitt (positiv nåverdi). Det vil med andre ord si at når aktører etablerer seg i markeder, er det fordi de tror de kan hente ut superprofitt i markedet. Det er litt nerdete, men jeg vil likevel si det. Det er litt morsomt at et effisient marked består av utrolig mange aktører som mener at markedet ikke er effisient.

Det jeg har forsøkt å gjøre her er å fortelle dere forskjellen mellom nåverdi og avkastning. Nåverdien er den avkastning vi får UTOVER det vi krever å få for at vi skal gå for dette prosjektet heller enn et alternativt prosjekt. Internrenten er den prosentvise avkastningen vi FAKTISK får. Er denne større enn avkastningskravet har vi positiv nåverdi, fordi avkastningen vi faktisk får er større enn den vi krever. Er internrenten mindre enn avkastningskravet får vi negativ nåverdi, og vi vil få bedre avkastning ved å investere pengene i alternative prosjekter. Har vi en internrente som er lik avkastningskravet blir nåverdien lik 0. Vi får ingen avkastning utover det vi krever, og det vi kan få alternativt.

Vil du dufte av selvtillit og suksess på eksamen?

Finn din nye duft hos

Vi benytter følgende tall til de neste oppgavene:

Nedenfor er vist et regnskapssammendrag for bedriften North Park ASA. Bedriften driver en mva-pliktig virksomhet.

Resultatregnskap for året	20×1
Driftsinntekter	70.000.000
Driftskostnader	58.000.000
Driftsresultat	12.000.000
Renteinntekter	150.000
Rentekostnader	2.050.000
Resultat før skattekostnad	10.100.000
Skattekostnad	2.727.000
Årsresultat	7.373.000

Balanse per 31.12.	20×1	20×0
Anleggsmidler	76.000.000	65.000.000
Omløpsmidler	30.000.000	25.000.000
Sum eiendeler	106.000.000	90.000.000

Egenkapital	33.700.000	30.000.000
Langsiktig gjeld	42.000.000	34.000.000
Kortsiktig gjeld	30.300.000	26.000.000
Sum egenkapital og gjeld	106.000.000	90.000.000

Tilleggsopplysninger:

Varelager 6.000.000 4.000.000

Kundefordringer 8.000.000 12.000.000

Leverandørgjeld 14.000.000 10.000.000

Varekostnad 31.000.000

Avskrivninger 11.000.000

Gevinst ved salg av brukte

anleggsmidler 120.000

Oppgave 7

Hva var totalkapitalens rentabilitet før skatt for North Park ASA i 20×1? Oppgi svaret i % (kun tallet) med en desimalers nøyaktighet, og bruk komma som desimaltegn.

Rentabilitet er en metode for å måle resultatet i bedriften opp i mot investert kapital. Når vi måler rentabiliteten til totalkapitalen, slik vi skal i denne oppgaven, måler vi bedriftens avkastning på den samlede kapitalen som er bundet i bedriften. Totalkapitalrentabiliteten vil dermed gi oss et tall på nivået på bedriftens inntjening, og hvor godt man har “drevet butikken”. Eller med andre ord: hvor effektiv bedriften har vært til å forvalte de ressursene de har.

Totalkapitalrentabiliteten beregnes slik:

(Driftsresultat + finansinntekter) / gjennomsnittlig totalkapital

I dette regnskapet er finansinntekter det samme som renteinntekter. Det er ofte det, så remember.

Oppgave 8
Hva var egenkapitalens rentabilitet før skatt for North Park ASA i 20×1? Oppgi svaret i % (kun tallet) med en desimalers nøyaktighet og bruk komma som desimaltegn.

Da vi regnet ut totalkapitalrentabiliteten (TKR) så vi hvordan den samlede kapitalen til bedriften forrentet seg. Nå skal vi se på egenkapitalens rentabilitet (EKR), som er veldig interessant for eierne og potensielle eiere av bedriften. Den viser hvordan eiernes investerte kapital utvikler seg. Dersom man står overfor en bedrift som er 100% finansiert av egenkapital (ingen gjeld), vil totalkapitalrentabiliteten og egenkapitalrentabiliteten være like stor. (Det er klare sammenhenger mellom EKR og TKR, og denne kan blant annet illustreres gjennom brekkstangformelen som du finner på side 454 i Sending-boka.) For deg som skal investere penger vil det kanskje være interessant å se hvilke av bedriftene du skal investere i som har høyest egenkapitalrentabilitet. Det som er viktig å huske er at eierne kommer sist når kapitalen skal fordeles. Først skal vareleverandørene, arbeidstakere, bankene osv. ha sine penger. Deretter, hvis det er noe til overs, går det til egenkapitalen.

Egenkapitalrentabiliteten bør som regel være høyere enn totalkapitalrentabiliteten. Dette fordi investorene som skyter inn pengene sine tar en mye høyere risiko enn f.eks. en produsent som selger en vare til bedriften. I tillegg bør den utvilsomt være bedre enn forventet avkastning på markedsporteføljen (f.eks. hovedindeksen på Oslo Børs). Dette fordi det er større risiko knyttet til å ha pengene sine i en virksomhet enn å ha pengene sine investert i hovedindeksen (mao mange bedrifter i forskjellige bransjer). Jo høyere risiko vi tar, jo høyere avkastning vil vi i sum kreve.

Vanligvis ønsker eierne å vite hvor mye av resultatet som går i deres “lomme”, derfor er det vanligste å beregne egenkapitalrentabiliteten etter skatt, men i denne oppgaven bes vi beregne den før skatt. Da er formelen slik:

ordinært resultat før skatt / gjennomsnittlig egenkapital

Gjennomsnittlig egenkapital får du ved å ta IB egenkapital + UB egenkapital og dele det på 2. IB EK er 30 mill. Hva er UB EK?

Oppgave 9
Alt varekjøp har skjedd på kreditt. Posten leverandørgjeld er i sin helhet gjeld til vareleverandører. Hva ble utbetalt til bedriftens vareleverandører i 20×1? Oppgi svaret (kun tallet) i kroner og bruk punktum som tusenskiller.

Husker dere sammenhengen jeg skrev om tidligere?
IB + tilkomst – avgang = UB
Altså: Balansepostens størrelse på starten av året + det som øker balanseposten – det som reduserer balanseposten = balansepostens størrelse på slutten av året

I denne sammenhengen vil varekjøp (på kreditt) gjøre at balanseposten “leverandørgjeld” øker (fordi du får MER gjeld). Du forstår også at hvis du betaler ned gjelda di, så vil balanseposten reduseres (fordi du får MINDRE gjeld).

MAO:
IB leverandørgjeld + innkjøp (inkl. mva) – Utbetalinger til leverandørene = UB leverandørgjeld

Du må huske å plusse på mva på innkjøpet, fordi leverandørgjeld-posten i balansen er inkludert mva (fordi det beløpet som står på fakturaen din er inkludert mva, hvis det gir mer mening)
Denne snur vi på og får følgende oppsett

IB leverandørgjeld + innkjøp (inkl. mva) – UB leverandørgjeld = utbetalinger til leverandører

Varekjøpet husker vi at vi finner ved å snu og vende på lagerligninga: Husk at vareforbruk er det samme som varekostnad (fordi, vi husker jo at en kostnad oppstår når vi forbruker).

Vareforbruk = IB varelager + Varekjøp – UB varelager
Altså:
Varekjøp = Vareforbruk – IB varelager + UB varelager

Husk at varekjøpet skal være inkl mva!

Da er det bare å regne da 🙂

Oppgave 10

Hva var gjennomsnittlig lagringstid for varene i 20×1? Oppgi svaret i hele dager (avrund oppover hvis det er nødvendig).

For å regne ut gjennomsnittlig lagringstid for varer kan man enten først beregne varelagerets omløpshastighet, og deretter dele 360 på denne summen, eller ta gjennomsnittlig varelager delt på varekostnad ganget med 360. Jeg skal presentere begge nedenfor. Hvorfor bruker vi 360 og ikke 365? Hvorfor er himmelen blå? Hvorfor kjører vi på høyre side av veien? Jeg vet ikke, det bare er sånn…

Når vi snakker om omløpshastigheten til et varelager, snakker vi om hvor mange ganger lageret “byttes ut” pr. år. Det er fint å ha en relativt høy omløpshastighet, da dette som regel betyr at man har mindre kapital bundet i et varelager som tar lang tid å omsette. Dessuten slipper man at varene på lageret blir gamle og taper seg i verdi.

For å beregne varelagerets omløpshastighet får du:

varelagerets omløpshastighet = varekostnad / gjennomsnittlig varelager

Igjen, gjennomsnittlig varelager er (IB varelager + UB varelager) / 2

Når du har funnet omløpshastigheten tar du:

360 / varelagerets omløpshastighet

En annen måte å løse det på, som kanskje går litt fortere

Gjennomsnittlig lagringstid for varer = (gjennomsnittlig varelager * 360) / varekostnad

Tallet du får som svar forteller oss hvor mange dager varene i snitt ligger på lager før de blir solgt.

Posted on 04.03.201910.06.2023

Bedriftsøkonomi og finans – arbeidskrav 7 (2019)

Her kommer nest siste arbeidskrav i dette faget. Det nærmer seg eksamen. Begynner dere å bli stressa? Det ville jeg ikke vært. Dette faget er veldig likt fra år til år, så hvis du har vært flink å bruke bloggen min, møte opp i forelesninger og i eventuelle øvinger på campus så er du godt rustet til å starte med mengdetrening etter hvert. Det ligger mange eksamenssett ute. Dere bør også løse eksamenssett i faget “finans og økonomistyring 1”, da det faget er identisk med deres (så å si).

Oppgave 1:
Industribedriften Latex AS produserer to produkter, X og Y. I 2. kvartal 2015 hadde bedriften en omsetning på kr 36.000.000 fordelt med 40% på X og 60% på Y. Dekningsgraden for X var 45%. Dekningsgraden for Y var 36%. Bedriftens faste kostnader utgjorde kr 12.040.000. Bedriftens variable kostnader er proporsjonale. Hva var bedriftens resultat (overskudd/underskudd) i 2. kvartal 2015? Oppgi svaret i hele kroner og bruk punktum som tusenskiller.

Freshe sneakers: Dette er skoene som gjelder i vår

Denne type oppgave kommer ofte på eksamen, da den tester deg i ganske mye.

Du skal her finne bedriftens resultat. Som jeg har sagt før er bedriftens resultat ganske enkelt: inntekt – kostnad. Eller sagt med andre ord: dekningsbidrag – faste kostnader (fordi dekningsbidrag jo er inntekt (omsetning) minus variable kostnader).

Én måte å sette opp denne oppgaven på er:

Omsetning produkt X: 36.000.000 * 0,4 = …
Omsetning produkt Y: 36.000.000 * 0,6 = …

Dekningsgraden er dekningsbidraget i prosent. Derfor finner du dekningsbidraget for produktene slik:

Dekningsbidrag produkt X = Omsetning produkt X * dekningsgrad produkt X
Dekningsbidrag produkt Y = Omsetning produkt Y * dekningsgrad produkt Y
= totalt dekningsbidrag.

Dermed gjenstår det bare å trekke fra de faste kostnadene, så har du resultatet ditt.

Oppgave 2
Industribedriften Latex AS produserer to produkter, X og Y. I 2. kvartal 2015 hadde bedriften en omsetning på kr 36.000.000 fordelt med 40% på X og 60% på Y. Dekningsgraden for X var 45%. Dekningsgraden for Y var 36%. Bedriftens faste kostnader utgjorde kr 12.040.000. Bedriftens variable kostnader er proporsjonale. Hva var bedriftens nullpunktomsetning i 2. kvartal 2015? Oppgi svaret i hele kroner, og bruk punktum som tusenskiller.

Nullpunktomsetning regnes ut med FK/DG, som vi vet. Når vi har flere produkter må vi finne en gjennomsnitlig dekningsgrad. Her har vi 2 produkter, som har både forskjellig omsetning, og forskjellig dekningsgrad. De bidrar med andre ord ulikt til både omsetning og resultat. Mange tenker at når vi skal finne gjennomsnittlig dekningsgrad, så tar vi 45+36 delt på 2, det blir feil ettersom de vektes forskjellig i produksjonen.

Vi må derfor finne gjennomsnittlig DG på følgende måte:

Total omsetning – totale variable kostnader / total omsetning

“MEN FAEN, VI VET JO IKKE DE VARIABLE KOSTNADENE DIN DRITTHOBBYØKONOM!!”

Greit nok, men total omsetning – totale variable kostnader er jo det samme som totalt dekningsbidrag. For dere som ikke ser sammenhengen mellom pris og omsetning enda:
Pris er prisen pr enhet. Denne kan f.eks. være 100 kroner. Når vi selger denne enheten har vi fått en økt omsetning på 100 kroner.
Total omsetning blir derfor omsetningen på alle varene vi har solgt. Det blir prisen pr enhet*antall enheter vi har solgt.
Derfor får vi altså at Total omsetning – totale variable kostnader / total omsetning blir det samme som:

Totalt dekningsbidrag / total omsetning
(ser du at denne ligner litt på formelen for DG pr enhet, bare at i stedet for å dele på pris, så deler du på total omsetning? Det er ikke tilfeldig.)

Jeg går frem sånn for å finne totalt DB:

Omsetning produkt X = 36.000.000 * 0,4 = 14.400.000
Dekningsbidrag produkt X = 14.400.000 * 0,45 = 6.480.000

Gjør det samme selv med produkt Y:
Omsetning produkt Y = …
Dekningsbidrag produkt Y = …

Totalt DB = DB produkt X + DB produkt Y

Gj.sn. DG = Totalt DB / total omsetning =

Da har du altså funnet gjennomsnittlig dekningsgrad, og er klar til å sette inn tallene i NPO-formelen: FK/DG

FK/DG = ??

Oppgave 3
En bedrift har i en periode solgt 1.000 enheter av sitt produkt til en pris av kr 500. Bedriften har proporsjonale variable kostnader som utgjør kr 200 per enhet. Faste kostnader utgjør kr 200.000 per periode. Maksimal kapasitet er 2.000 enheter. Markedsundersøkelser tyder på at priselastisiteten er -2,2. I hvilken retning og med hvilket beløp vil bedriftens resultat bli endret hvis bedriften reduserer prisen med 10 %? Hvis resultatet forbedres, angis resultatforbedringen uten fortegn. Hvis resultatet forverres, angis resultatnedgangen med negativt fortegn. Oppgi svaret (kun tallet) i kroner uten desimaler og bruk punktum som tusenskiller.
Priselastisitet sier noe om hvor følsom etterspørselen etter et produkt er for pris. Sånn egentlig er elastisitet en individuell greie. Min følsomhet til prisen på en mac vil kanskje være annerledes enn din. Fordi jeg er rikere enn deg, spør du? Nja, kanskje, kanskje ikke. Det handler like mye, om ikke mer, om hvor mye nytte vi ser i produktet. Når vi regner priselastisitet i dette faget er det summen av alle individenes følsomhet vi snakker om.

Når priselastisiteten er -2,2 betyr det at når prisen stiger med 1 prosent, synker etterspørselen med 2,2 prosent. Hvis prisen synker med 10% stiger etterspørselen med 22%.

Når du skal regne ut dette trenger du egentlig bare å se på endring i dekningsbidrag. Endringen i dekningsbidrag vil være det samme som endringen i resultat, da de faste kostnadene vil være uendret.

Det jeg gjør først er å regne ut dekningsbidraget før prisreduksjon:

(Pris – VEK)*antall enheter solgt
(500-200)*1000 = 300.000 = total DB før prisreduksjon

Så vet vi at de skal redusere prisen med10%. Da vet vi, ettersom priselastisiteten er -2,2 at etterspørselen vil øke med 22% (10*2,2).

Da regner vi ut DB etter prisreduksjon slik (ja, jeg har gjort det slik at du må tenke litt selv):

(Pris*(1-0,10) – 200)*(1000*???) = total DB etter prisreduksjon

Nå skal du kunne finne resultatendringen

Oppgave 4
En bedrift har per 31.12.20×1 kr 12.000.100 i omløpsmidler, kr 13.000.000 i kortsiktig gjeld, kr 16.100.000 i langsiktig gjeld og kr 12.690.000 i egenkapital. Hva er beløpet for bedriftens anleggsmidler? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

AM + OM = EK + LG + KG

Hvis denne ligningen virker gresk for deg, er det fornuftig å bruke et par linjer på å repetere hva balansen er, og hva den skal gi uttrykk for.

Balanseligningen skal gi uttrykk for hvilke økonomiske ressurser bedriften har på et bestemt tidspunkt, og hvordan ressursene er finansiert. Altså viser balansen den finansielle stillingen på et gitt tidspunkt, mens resultatregnskapet til sammenligning viser resultatet av finansiell aktivitet over en gitt periode. Grunnen til at jeg nevner resultatregnskapet er fordi ofte når man leser regnskapet til en bedrift er det som regel rapportert i all hovedsak med resultatregnskapet og balansen.

Balansen deler vi opp i to «avdelinger» eller som vi i praksis skal benytte, to sider av en ligning. Aktiva-siden, som er ressursene dine, og passiva-siden, som er finansieringen av ressursene.

Vi kan altså skrive balanseligninga slik:
#1: Ressursene i en bedrift = finansieringen av ressursene
#2: Anvendelse av kapital = anskaffelse av kapital
#3: Eiendeler er = egenkapital + gjeld
#4: Anleggsmidler + Omløpsmidler = Egenkapital + Langsiktig gjeld + Kortsiktig gjeld
#5: AM + OM = EK + LG + KG

Egenkapitalen kan vi igjen dele opp i «Opptjent egenkapital» (Egenkapital som er opptjent ved at bedriften har gått i overskudd, uten å betale ut alt overskuddet i utbytte) og «Innskutt egenkapital» (egenkapital som er skutt inn av investorer). For å gjøre det enklest benytter vi:

AM + OM = EK + LG + KG

Løs oppgaven som en ligning med en ukjent.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077

Oppgave 5
En bedrift betalte kr 273.900 i diverse driftskostnader i 2015. Per 01.01.2015 hadde bedriften ubetalte driftskostnader fra 2014 for kr 19.200. Per 31.12.2015 viste det seg at av driftskostnader betalt i 2015 var kr 11.100 forskuddsbetaling for 2016. Hva ble resultatført som driftskostnader i resultatregnskapet i 2015? Se bort fra mva i denne oppgaven. Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

Dette er repetisjon. Dette er periodisering. Dette kan du. (Hvis ikke: se tidligere innlegg fra arbeidskrav med samme type oppgaver) 🙂

Oppgave 6

Bedriften Kongsberg Lion AS produserer to produkter. Selvkostkalkylen for produktene ser slik ut:

	Produkt A	Produkt B
Direkte materialer	2 400,00	14 400,00
Direkte lønn	1 800,00	20 000,00
Indirekte variable kostnader i tilvirkningen (30 %)	540,00	6 000,00
Indirekte faste kostnader i tilvirkningen (50 %)	900,00	10 000,00
Totale tilvirkningskostnader	5 640,00	50 400,00
Indirekte variable kostnader i salg/adm (10 %)	564,00	5 040,00
Indirekte faste kostnader i salg/adm (30 %)	1 692,00	15 120,00
Selvkost	7 896,00	70 560,00

Produksjon og salg i en normalperiode er 1 000 enheter av produkt A og 100 enheter av produkt B. Selvkostkalkylen er basert på disse produksjonsmengdene. Salgspris per enhet er kr 8 000 for A og kr 80 000 for B. Det medgår 20 kg materialer (råvarer) per enhet A og 120 kg materialer (råvarer) per enhet B. Arbeidstidsforbruket per enhet A er 9 timer og per enhet B 100 timer.

Anta at bedriften i en periode har begrenset tilgang på materialer slik at materialer er en flaskehals. Det kan maksimalt skaffes 19 920 kg materialer. Bedriften ønsker i denne perioden å satse på det produktet som er mest lønnsomt gitt begrensningen i tilgangen på materialer.

Hvor stort blir totalt dekningsbidrag for perioden hvis bedriften kun produserer det produktet som er mest lønnsomt? Oppgi svaret (kun tallet) i kroner, og bruk punktum som tusenskiller.

Ja, okei. Endelig noen flaskehalsoppgaver. En flaskehals er et fellesbegrep for knappe faktorer en bedrift kan oppleve, som f.eks. tilgang til råvarer, arbeidskraft, hylleareal eller i vårt tilfelle, maskinkraft. Når vi ser på flaskehalsproblemer i dette faget, prioriteres de produktene som gir høyest dekningsbidrag per flaskehalsenhet.

I slike oppgaver blir vi egentlig bedt om å tegne opp et kapasitetsdiagram, men det slipper vi i denne oppgaven, fordi vi får informasjon om at vi egentlig bare har med én flaskehals å gjøre – råvarene.

Jeg har et standard oppsett jeg alltid setter opp når jeg får slike oppgaver, fordi på eksamen kan du få presentert informasjonen på mange forskjellige måter. Hvis du har et standardoppsett som du er trygg på vet du at du klarer å løse oppgaven på eksamen, uansett hvordan de har valgt å formulere oppgaveteksten. Denne oppgaven er litt spesiell, slik at oppsettet mitt vil ikke se veldig lurt ut, men jeg vil likevel presentere oppsettet for dere, så kan dere bruke det på andre flaskehalsoppgaver dere skal løse senere.

Først oppsummerer jeg informasjonen:

Begrensning	Forbruk produkt A	Forbruk produkt B	Kapasitet
Råvarer	20	120	19920
Arbeidstimer	9	100	Ikke relevant*

*Jeg har skrevet ikke relevant. Grunnen til det er at de skriver at råvarer er flaskehalsen. Jeg velger å tolke det dithen at arbeidstimene ikke er en flaskehals, fordi man vil bli begrenset av kapasitetsbegrensningen på råvarer før kapistetsbegrensingen på arbeidstimer blir et problem. For å lage et bilde du kanskje forstår: Hvis du har 2 motorsager og 3 arbeidsfolk, så er flaskehalsen din motorsagene. Arbeidsfolka er en begrensning, men de er ikke en flaskehals, fordi akkurat nå, med 2 motorsager, er ikke begrensningen på arbeidsfolk et problem – motorsagene er det.

Deretter setter jeg opp dette oppsettet, og hvor mye jeg maksimalt kan produsere av henholdsvis produkt A og B dersom jeg KUN produserer ett av de. Det gjør jeg ved å bruke formelen: kapasitet / forbruk pr enhet

Begrensning	Kun A	Kun B	Kapasitet
Råvarer	19920/20=996	19920/120=166	19920
Arbeidstimer	Kan ikke regne ut	Kan ikke regne ut	Ikke oppgitt

Dette betyr at hvis vi BARE produserer produkt A, og benytter all råvaren vår til produksjonen av produkt A, kan vi produsere 996 enheter av produkt A. Dersom vi kun produserer B kan vi produsere 166 enheter av produkt B.

Da må vi se hva som gir oss mest dekningsbidrag: 996 av produkt A, eller 166 av produkt B.
Totalt dekningsbidrag = (Pris – VEK)*antall enheter
VEK pr enhet A og pr enhet B kan vi lese av i kalkylen. Det er min oppfatning at veldig mange av dere sliter med å skille hva som er variable og hva som er faste kostnader. Det skal egentlig være helt unødvendig å feile på. Direkte material og direkte lønn er material- og lønnskostnader som medgår direkte i produktet. Det betyr at hvis man IKKE hadde produsert produktet ville ikke kostnadene medgått. Ergo, de er variable, fordi én ekstra enhet fører til ekstra kostnad. De indirekte variable ligger i navnet at er variable.

Jeg vil at dere skal forstå forskjellen på faste og variable kostnader, men likevel skal gjøre det jævlig enkelt for dere: I denne selvkostkalkylen, og i dette faget generelt er ALLE kostnader variable, så lenge det ikke står at de er faste (eksempelvis indirekte faste kostnader)

VEK for produkt A blir derfor: 2400 (DM) +1800 (DL) + 540 (IVK tilvirkning) +564 (IVK salg og admin) = 5.304

Totalt dekningsbidrag produkt A = (8.000 – 5.304)*996 = 2.685.216
Totalt dekningsbidrag produkt B = ??

Hvilket produkt gir best DB, og hvor mye blir det?

Oppgave 7
Til en ordre forventes å medgå direkte materialkostnader for kr 55.000 og direkte lønnskostnader for kr 60.000. Tilleggssatsene for indirekte variable kostnader er 20% i tilvirkningsavdelingen og 10% i salgs- og administrasjonsavdelingen. Aktivitetsmål ved innkalkulering av indirekte variable kostnader er direkte lønnskostnader i tilvirkningsavdelingen og variable tilvirkningskostnader i salgs- og administrasjonsavdelingen. Dekningsgraden er 40%. Beregn salgspris uten mva for ordren. Oppgi svaret (kun tallet) i hele kroner uten desimaler, og bruk punktum som tusenskiller.
Jeg skriver det samme som jeg gjorde i mitt forrige innlegg. Legg merke til at tallene i figurene under er annerledes enn tallene i oppgaven, da disse figurene ble laget til en oppgave med andre tall.

Dette er oppsettet for bidragskalkyle. En bidragskalkyle inneholder bare de variable kostnadene (i motsetning til selvkostkalkylen som inkluderer de faste kostnadene også)

Direkte material
Direkte lønn
Indirekte variable kostnader (IVK), tilvirkning
=variable tilvirkningskostander
Indirekte variable kostnader, salg og administrasjon
=minimumskost

Noen ord om de indirekte kostnadene. Direkte kostnader er jo kostnader som kan knyttes direkte til “kostnadsbærerne”. Dette er ting som material og lønn. Det er lett å knytte stoffet og knappene på skjorta til skjorta. Det samme gjelder lønn. Det er lett å knytte lønnskostnadene til skjorta, ettersom vi vet hvor mye tid arbeiderne bruker på å produsere skjortene. De indirekte kostnadene er kostnader vi ikke kan knytte direkte til det bestemte produktet. Dette kan f.eks. være husleie, strøm, lønn til sjefen (som ikke har noe direkte med produksjonen av produktet å gjøre), avskrivninger, arbeidsgiveravgift osv, osv osv…

Direkte kostnader er altså kostnader som oppstår som en direkte konsekvens av produksjonen av en vare, mens indirekte kostnader er skjønnsmessig fordelt. Disse indirekte kostnadene er kostnader vi er nødt til å fordele på en eller annen måte. I dette faget fordeles de vanligvis ved en fast prosentsats. Denne prosentsatsen er knyttet opp mot et “aktivitetsmål”. I denne oppgaven er prosentsatsen for de indirekte variable kostnadene i tilvirkningsavdelingen 20%, og aktivitetsmålet er direkte lønn. Det betyr at IVK i tilvirkningen er 20% av direkte lønn. Tilleggssatsen for IVK i salg og admin er 10% av de variable tilvirkningskostandene.

I tillegg skal bedriften ha en dekningsgrad på 40%. Dekningsgraden er dekningsbidraget i prosent. Dekningsbidrag skal, som det ligger i ordet: dekke de faste kostnadene, og bidra til et overskudd. Dekningsbidrag.

Jeg vil forsikre meg om at dere har forstått en vesentlig sammeneheng i dette faget. Når jeg skal lære bort denne sammenehengen, syns jeg det er enklest å gjøre det slik (OBS! TALLENE I DETTE EKSEMPLET STEMMER IKKE MED TALLENE I OPPGAVEN):

Se for deg at prisen på et produkt består av 3 deler. De variable kostnadene (VK), de faste kostnadene (FK) og et overskudd (π).

Den delen av prisen som dekker de faste kostnadene og bidrar til overskudd er altså det vi kaller dekningsbidrag. Dersom dette er oppgitt til å være 35%, vet vi at resten, altså de variable kostnadene er 65%. Dette er ikke tilfellet i denne oppgaven, men jeg orker ikke tegne nye figurer. I denne oppgaven er dekningsgraden 40%, som betyr at de variable kostnadene utgjør 60%

Så. når du har regnet ut minimumskosten, så vet du at du har funnet de variable kostnadene. Du vet videre at dette må være 65% av totalen, ettersom DG er 35%

Da må du spørre deg selv. “Hva er dette 65% av?”, så regner du ut det. Da har du svaret.

Sett opp en bidragskalkyle for oppgaven vår, og regn så ut salgsprisen ved hjelp av sammenhengen overfor. Husk at vi har en DG på 40%, og ikke 35% som i eksemplet over 🙂

Vil du dufte av selvtillit og suksess på eksamen?

Finn din nye duft hos

Oppgave 8
En bedrift har i en periode solgt 12.800 enheter av sitt produkt til en pris av kr 1000. Bedriften har proporsjonale variable kostnader som utgjør kr 750 per enhet. Faste kostnader utgjør kr 2.500.000 per periode. Markedsundersøkelser tyder på at ved en prisøkning på 10 % vil bedriftens overskudd forbedres med kr 25.600. Hva er priselastisiteten ved denne prisøkningen? Oppgi svaret (kun tallet med fortegn) med en desimalers nøyaktighet. Bruk komma som desimaltegn.

Priselastisiteten finner vi ved å ta: prosentvis endring i mengde / prosentvis endring i pris.

Prisøkningen har vi. Den er 10 prosent

For å finne endring i mengde må vi gjøre litt matte.
Vi vet at de tidligere har hatt følgende resultat:

(Pris – VEK) * antall enheter solgt – faste kostnader = resultat
(1000-750)*12800 – 2.500.000 = 700.000
Vi vet at den nye prisen blir 1.000*1,10, og at VEK fremdeles er 750 kroner. Da sitter vi igjen med 350.
Vi vet at de faste kostnadene er 2.500.000. Det vi trenger å finne er mengden. Vi vet, jamfør resultatligningen at

(pris-VEK)*antall enheter solgt – FK = resultat
I oppgaveteksten står det at resultatet skal øke med 25.600, som betyr at nytt resultat blir 725.600

Hvis vi setter inn tallene vi har, og løs ligningen med hensyn på X (antall enheter solgt):
(1100 – 750) * X – 2.500.000 = 725.600
Som sagt finner vi elastisiteten slik:

e_p = Relativ mengdeendring / Relativ prisendring

som rent teknisk kan uttrykkes slik:

e_p = [(X₂ – X₁)/X₁] / [(P₂ – P₁)/P₁]

Hvor X₂ er den nye mengden, X₁ er den gamle mengden, P₂ er den nye prisen og P₁ er den gamle prisen.

[(X₂ – X₁) / X₁] er altså den relative mengdeendringen. [(P₂ – P₁) / P₁] er den relative prisendringen.

Mengdeendringen i prosent finner vi med andre ord slik

X₂ – 12.800 / 12.800 (X₂ er det du fant ved hjelp av resultatligning 2 lengre oppe)

Da har du alt du trenger for å regne ut elastisiteten. Husk fortegn! 🙂

Oppgave 9
En bedrifts årsregnskap for 2015 viste et driftsresultat på kr 11.271.000. Det framgår ikke av regnskapet at bedriften per 01.01.2015 hadde skjulte reserver i sine eiendeler for kr 426.000 og per 31.12.2015 skjulte reserver for kr 233.000. Hva var bedriftens korrekte driftsresultat i 2015? Oppgi svaret i hele kroner (kun tallet), og bruk tusenskiller.

Jeg skriver det samme som jeg har skrevet i tidligere innlegg:

Mange syns dette med skjulte reserver er litt vanskelig, fordi boka forklarer det litt for komplisert for mange. Helt enkelt forklart er en skjult reserve en positiv forskjell mellom den virkelige verdien, og den balanseførte verdien av en eiendel. Man kan også få skjulte reserver i gjeld, men da hvis den virkelige gjelden er lavere enn den balanseførte.

Det vi kan resonere oss fram til er at dersom det viser seg at vi har lavere gjeld eller større verdi på anleggsmidler eller omløpsmidler enn vi trodde, vil dette påvirke egenkapitalposten i balansen vår. Egenkapitalen vil øke.

De oppgavene dere får er ofte sammensatt av informasjon om skjulte reserver over x antall år, og viser hvordan den skjulte reserven øker, synker eller forholder seg lik over tid. Det som er viktig å merke seg da er at hvis en skjult reserve forholder seg uendret fra et år til et annet, vil ikke dette påvirke resultatet. Dette fordi økningen av egenkapitalen er like stor ved inngangen som utgangen av året. Hvis vi ser en reduksjon i skjulte reserver (som i vår oppgave) vil det reelle resultatet være dårligere enn det fremstår. Hvis vi ser en økning i skjulte reserver er det reelle resultatet bedre enn det som fremstår i regnskapet.

Så, det var teorien. Hvordan skal vi løse slike oppgaver? Jo, det finnes en veldig enkel fasit, og den er som følger (VIKTIG, kommer ofte på eksamen!):

Skjulte reserver UB 2014 = 426.000
Skuljte reserver UB 2015 = 233.000
Endring skjulte reserver = 193.000 (reduksjon)

Bokført driftsresultat 2014= 11.271.000
Endring i skjulte reserver = ???
Virkelig driftsresultat 2014 = ???

Oppgave 10
En bedrift kjøpte ved inngangen til år 20×1 en maskin for kr 5.200.000. Antatt restverdi ved utløpet av levetiden var kr 400.000. De årlige avskrivninger (lineære avskrivninger) ble beregnet til kr 600 000. Hvor mange år har bedriften lagt til grunn som levetid for maskinen? Svaret (kun tallet) oppgis som antall hele år.

Du husker formelen for lineære avskrivinger:

Årlige avskrivinger = (Anskaffelseskost – utrangeringsverdi) / forventet levetid

Her har du en ligning med én ukjent.

600.000 = (5.200.000 – 400.000) / X

Posted on 04.03.201910.06.2023

Bedriftsøkonomi og finans – arbeidskrav 6 (2019)

Håper alt står bra til. Her er arbeidskrav 6. Som før, glad for tilbakemeldinger. Jeg setter også pris på at dere stiller spørsmål, og at dere hjelper hverandre i kommentarfeltet. Det finnes ikke dumme spørsmål – bare dumme folk, som jeg pleier å si, hihi!

Oppgave 1
Varehandelsbedriften PBL AS budsjetterer for en periode med salgsinntekter uten mva på kr 3 000 000. Vareforbruket er beregnet til kr 1 740 000. Diverse kostnader som lønn, telefon, husleie osv forventes å bli kr 900 000. Hva er budsjettert bruttofortjeneste i %? Oppgi svaret (kun tallet) i nærmeste hele prosent.

Bruttofortjeneste er forskjellen mellom salgspris og varekostnad, og viser med andre ord hvor mye man tjener på å selge en vare.

Bruttofortjeneste er på en måte varehandelens dekningsbidrag, altså pris minus variable kostnader (beregningen av dekningsbidraget inkluderer også andre variable kostnader enn varekostnaden, dog). Du kan klare å resonere deg frem til at vareforbruket er de variable kostnadene i en varehandelsbedrift. Fordi jo flere varer du selger, jo større kostnad får du ved at du må ta ut varer fra lageret. De varierer altså med antall solgte enheter = variabel kostnad.

Inntekten er omsetningen din. La oss se for oss en bedrift som kun selger én type vare til én pris. Da er inntekten (omsetningen): antall enhter solgt * pris. Bruttofortjenesten din i denne oppgaven er med andre ord inntekt – variable kostnader. Du skal imidlertid oppgi bruttofortjenesten i prosent av salgsprisen. Med andre ord: bruttofortjeneste / salgspris

Oppgave 2
Skattum Netting AS skal sette opp en bidragskalkyle for en ordre. Bedriften forventer at direkte materialkostnader vil bli kr 8.000. Direkte lønnskostnader forventes å bli kr 10.000. Bedriften har delt inn sin virksomhet i to kostnadssteder; tilvirkningsavdelingen og salgs- og administrasjonsavdelingen. Tilleggssatsen for indirekte variable kostnader er i tilvirkningsavdelingen 28 % . Aktivitetsmål er direkte lønn. Tilleggssatsen for indirekte variable kostnader i salgs- og administrasjonsavdelingen er 10%. Aktivitetsmål er totale variable tilvirkningskostnader. Bedriftens krav til dekningsgrad er 35%.

Beregn salgspris uten mva for ordren. Oppgi svaret (kun tallet) i nærmeste hele kroner og bruk punktum som tusenskiller.

Dette er oppsettet for bidragskalkyle. En bidragskalkyle inneholder bare de variable kostnadene (i motsetning til selvkostkalkylen som inkluderer de faste kostnadene også)

Direkte material
Direkte lønn
Indirekte variable kostnader (IVK), tilvirkning
=variable tilvirkningskostander
Indirekte variable kostnader, salg og administrasjon
=minimumskost

Direkte kostnader er altså kostnader som oppstår som en direkte konsekvens av produksjonen av en vare, mens indirekte kostnader er skjønnsmessig fordelt. Disse indirekte kostnadene er kostnader vi er nødt til å fordele på en eller annen måte. I dette faget fordeles de vanligvis ved en fast prosentsats. Denne prosentsatsen er knyttet opp mot et “aktivitetsmål”. I denne oppgaven er prosentsatsen for de indirekte variable kostnadene i tilvirkningsavdelingen 28%, og aktivitetsmålet er direkte lønn. Det betyr at IVK i tilvirkningen er 28% av direkte lønn. Tilleggssatsen for IVK i salg og admin er 10% av de variable tilvirkningskostandene.

I tillegg skal bedriften ha en dekningsgrad på 35%. Dekningsgraden er dekningsbidraget i prosent. Dekningsbidrag skal, som det ligger i ordet: dekke de faste kostnadene, og bidra til et overskudd. Dekningsbidrag.

Visste du forresten at BI har en egen podcast som produseres på Campus Trondheim som heter Dekningsbidraget?

Jeg vil forsikre meg om at dere har forstått en vesentlig sammeneheng i dette faget. Når jeg skal lære bort denne sammenehengen, syns jeg det er enklest å gjøre det slik:

Så. når du har regnet ut minimumskosten, så vet du at du har funnet de variable kostnadene. Du vet videre at dette må være 65% av totalen, ettersom DG er 35%

Da må du spørre deg selv. “Hva er dette 65% av?”, så regner du ut det. Da har du svaret. Hvis jeg f.eks. ville funnet ut hva 45 er 30 prosent av, vill jeg gjort slik:
45/0,30 = 150. 45 er altså 30% av 150
Oppgave 3
Varehandelsbedriften Geiger AS har en periode budsjettert med en salgsinntekt på kr 3.036.000 uten mva. Forventet vareforbruk er kr 2.200.000. Hva er budsjettert avanse i %? Oppgi svaret (kun tallet) i hele prosent.

Avansen er som bruttofortjenesten, salgsinntekt – varekostnad. Forskjellen mellom bruttofortjeneste og avansen er at når vi regner den i prosent, regner vi bruttofortjenesten i forhold til salgsinntekt. Når vi regner avansen i prosent, regner vi den derimot i forhold til innkjøpsprisen (varekostnaden).

Jeg sier altså at avansen er salgsinntekt – varekostnad. Varekostnad husker vi er det samme som vareforbruk. Formelen blir følgende:
Avanse i prosent = avanse i kroner / varekostnad

Vil du dufte av selvtillit og suksess på eksamen?

Finn din nye duft hos

Oppgave 4
Varehandelsbedriften LLC AS budsjetterer for en periode med en total salgsinntekt kr 45.000.000. Totale kostnader (som er sammensatt av både faste og variable kostnader) er forventet å utgjøre 90% av salgsinntekten. Budsjettert dekningsgrad er 45%. Hva er budsjettert nullpunktomsetning? Oppgi svaret i hele kroner (kun tallet) og bruk punktum som tusenskiller.

Det kan sikkert virke som en uoverkommelig oppgave, men slapp av. Den er ikke så vanskelig. Vi skal finne nullpunktsomsetningen, og den finner vi ved:

NPO = FK / DG

Lær deg dette. Du får det garantert på eksamen, så denne formelen må du kunne.

Så til oppgaven.

Du vet at total salgsinntekt er 45.000.000 kroner, og at de totale kostnadene er 90% av dette, altså 40.500.000. Du har i tillegg fått oppgitt en dekningsgrad på 45%. Hvis du ser på den sammenhengen jeg beskrev i oppgave 2, vil du kunne klare å resonere deg frem til at 45.000.000 er 100% av inntekten din. Når dekningsgraden er 45% må med andre ord de variable kostnadene være…?

Når lyset har gått opp for deg, vil du ha funnet de variable kostnadene. Da finner du de faste kostnadene ved å ta:
Totale kostnader (altså 40.500.000) minus de variable kostnadene. Nå har du alt du trenger for å regne ut nullpunktsomsetningen, som jeg gjentar at du finner ved:

FK / DG

NBNBNB: Husk å oppgi DG som 0,45 – ikke 45!

Oppgave 5
Varehandelsbedriften Teabone AS budsjetterer for en periode med faste kostnader på kr 10.880.000. Målsatt omsetning er kr 28.000.000, og målsatt overskudd kr 2.000.000. Hva er budsjettert dekningsgrad? Oppgi svaret (kun tallet) i hele prosent.

Vi ser på denne igjen (merk at dette er tallene fra den forrige oppgaven, og ikke denne). Omsetningen (28.000.000) er altså 100%. Faste kostnader og overskudd utgjør dekningsbidraget. Dekningsgraden er DB i prosent av omsetning.

Denne greier du, søta 🙂

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077

Oppgave 6
Neste periode budsjetterer Teabone AS med faste kostnader på kr 12.000.000. Budsjettert overskudd er kr 4.000.000, og budsjettert dekningsgrad er 40%. Hva er budsjettert salgsinntekt? Oppgi svaret (kun tallet) i hele kroner og bruk punktum som tusenskiller.

OBS, tallene i tegningen er de samme som i oppgave 2. Orket ikke bytte ut tallene med de fra denne oppgaven.

Prøv selv’a <3

Oppgave 7

En bedrift produserer bare ett produkt og har følgende selvkostkalkyle per enhet av produktet:

Salgspris 80.000

Direkte material 40.000

Direkte lønn 18.000

Indirekte variable kostnader 5.000

Indirekte faste kostnader 7.000

Selvkost 70.000

Fortjeneste 10.000

Kalkylen er basert på en total produksjon (= salg) på 1 200 enheter per periode. De faste kostnadene er driftsuavhengige innenfor produksjonskapasiteten på 1 400 enheter.

For kommende periode antar bedriften at produksjon og salg vil bli 1 050 enheter. Beregn budsjettert resultat (overskudd/underskudd). Oppgi svaret i hele kroner (kun tallet), og bruk tusenskiller.

Nå skal jeg lære dere en sammenheng som dere vil ha bruk for:

(Pris-VEK)*antall enheter solgt – FEK*normalproduksjon = resultat

Denne MÅ du huske.

Når jeg sier normalproduksjon mener jeg den produksjonen de har basert kalkylen på (i dette tilfellet 1200 enheter). Grunnen til at du ganger FEK med normalproduksjon er at du da finner de totale faste kostnadene i virksomheten, og den vil forbli uforandret selv om du produserer/selger flere eller færre enheter. Dekningsbidraget ditt (pris-vek) må du derimot gange med det du FAKTISK selger. Du kan si at det er dekningsbidraget ditt som utgjør resultateffekten ved salg av én ny enhet, ettersom FK ikke påvirkes.

Oppgave 8
En bedrift forbrukte i en gitt periode råvarer for kr 41.000. Det var råvarer på lager ved periodens begynnelse for kr 7.500. Beholdningen av råvarer ved periodens slutt var kr 8.800. Hva var bedriftens råvarekjøp inkl. mva i perioden? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

Bruk sammenhengen jeg har lært dere tidligere. Husker du ikke denne, gå tilbake til et tidligere arbeidskravinnlegg, og les hva denne sammenhengen betyr:

IB + tilkomst – avgang = UB

Oversatt til lagersammenheng:

IB lager + varekjøp – vareforbruk = UB lager

Husk å legge på mva, slik oppgaven spør om.

Oppgave 9
Mosvika Glass- og snekkerverksted AS har budsjettert med følgende kostnader for året 20×1: Direkte materialkostnader kr 5 000 000, direkte lønnskostnader kr 6 000 000, indirekte variable kostnader kr 1 200 000 og indirekte faste kostnader kr 3 480 000. Bedriften benytter budsjettallene til å beregne tilleggssatser for indirekte kostnader til bruk i sine kalkyler for enkeltordrer. Bedriften benytter én tilleggssats for indirekte variable kostnader og én tilleggssats for indirekte faste kostnader. Direkte lønnskostnader er aktivitetsmål. Hva blir tilleggssatsen for indirekte faste kostnader? Oppgi svaret (kun tallet) i nærmeste hele prosent.

Mosvika ja. Fun fact: Mosvik kommune og Inderøy kommune slo seg sammen i januar 2012, og festen for denne sammenslåingen var mitt første betalte oppdrag som konferansier.

Det de ønsker at du skal gjøre her å vise at du har skjønt hvor den prosentsatsen du ofte får oppgitt i oppgavene (som f.eks i oppgave 2 i dette arbeidskravet) kommer fra. Her er det oppgitt at aktivitetsmålet for tilleggsatsene er lønnskostnader. Måten du da finner prosentsatsen generelt (dersom det ikke sier seg selv), er ved å ta

årsbudsjett / aktivitetsmål

Med andre ord, for denne oppgaven: de indirekte faste kostnadene delt på direkte lønn.

Oppgave 10
Industribedriften North Park AS har følgende sammenheng mellom kostnader i millioner kroner og produksjonsmengde i antall enheter:

Produksjonsmengde	0	1000	2000	3000	4000	5000	6000
Kostnader	3	4	4,9	5,7	6,4	7	7,5

Hvilken type variable kostnader har bedriften? Oppgi bokstaven for det svaralternativet nedenfor som du mener er korrekt.

a. Underproporsjonale variable kostnader

b. Proporsjonale variable kostnader

c. Overproporsjonale kostnader

Dette er en oppgave som ofte kommer på eksamen. Meningen med oppgaven er å teste at du forstår hvordan variable kostnader kan forløpe seg. Jeg skal forklare de 3 alternativene, så skal du få “gjette” hva riktig svar er.

Når vi snakker om underproporsjonale variable kostnader, snakker vi om kostnader som vil forløpe seg slik (ja, jeg bruker Paint. Deal with it):

Her har vi prisen på Y-aksen, og kvantum på X-aksen. Som du ser er prisen pr. enhet lavere ved større kvantum. Det vil med andre ord si at dersom vi øker produksjonsmengden med 100%, vil kostnaden øke med mindre enn 100% Dette kan f.eks. være grunnet kvantumsrabatt på innkjøpspris. Eller ta f.eks. et bakeri. Etterhvert som du baker mange kaker blir du mer og mer effektiv, og du søler mindre kakestrø på gulvet (svinn). Da blir kostnaden lavere pr. produserte kake i det lange løp.

Når vi snakker om proporsjonale variable kostnader, tar vi utgangspunkt i at de variable kostnadene er de samme pr enhet. Altså at du som baker bruker akkurat like mye tid på hver kake, og at du har akkurat like mye mel og sukker i hver kake. Dersom produksjonen øker med 100% vil også kostnadene øke med 100%

Den siste er overproporsjonale variable kostnader. Dette er kostnader som øker mer enn produksjonsmengden

Dette betyr at dersom vi øker produksjonen med 10% vil kostnadene stige med mer enn 10%. Eksempler på dette kan være at dersom produksjonen øker, så må de ansatte være lengre på jobb, og at du må betale overtidstillegg. Et annet eksempel kan vi hente fra deg gode gamle uttrykket “jo flere kokker, jo mere søl”. Det er ikke sikkert at “kokkene” klarer å opprettholde sin effektivitet dersom de blir flere når arbeidsmengden øker.

Sees neste uke til nytt arbeidskrav!

Love,
Petter K

Posted on 04.03.201910.06.2023

Bedriftsøkonomi og finans – arbeidskrav 5 (2019)

Hei hå! Her kommer min lille hjelper til dere i arbeidskrav 5. Setter pris på at dere hjelper hverandre i kommentarfeltet, da jeg er litt presset på tid.

Vi bruker følgende tall til de neste oppgavene

Nedenfor er vist et regnskapssammendrag for bedriften Tombstone ASA. Bedriften er mva-pliktig.

Resultatregnskap for året	2015
Driftsinntekter	84 000 000
Driftskostnader	60 000 000
Driftsresultat	24 000 000
Renteinntekter	600 000
Rentekostnader	3 000 000
Resultat før skattekostnad	21 600 000
Skattekostnad	5 832 000
Årsresultat	15 768 000

Balanse per 31.12.	2015	2014
Anleggsmidler	60 000 000	50 000 000
Omløpsmidler	48 000 000	40 000 000
Sum eiendeler	108 000 000	90 000 000

Egenkapital	45 000 000	35 000 000
Langsiktig gjeld	25 000 000	15 000 000
Kortsiktig gjeld	38 000 000	40 000 000
Sum egenkapital og gjeld	108 000 000	90 000 000

Tilleggsopplysninger:

Varelager 6 600 000 4 400 000

Kundefordringer 8 800 000 13 200 000

Leverandørgjeld 14 000 000 11 000 000

Varekostnad 34 000 000

Avskrivninger ?

Gevinst ved salg av brukte

anleggsmidler 96 000

Spørsmål 1

Hvor mye ble avsatt til utbytte per 31.12.2015? Oppgi svaret i kroner (kun tallet), og bruk punktum som tusen skiller.

Vi har tidligere sett på denne sammenhengen, som kan brukes til veldig mye.

IB + tilkomst – avgang = UB
For den som trenger å få det inn med teskje. Det denne ligninga sier er:
Så mye hadde jeg (IB) + så mye fikk jeg (tilkomst) – så mye ga jeg bort (avgang) = så mye har jeg igjen (UB).

Tilkomst er det som gjør at beholdningen/balanseposten blir større.
Avgang er det man kvitter seg med, og som følgelig gjør at beholdningen eller balanseposten blir mindre.

Denne kan også brukes her, og da må vi spørre oss selv, hva er “tilkomsten” og “avgangen” her?

Hvordan er det vi får tilkomst til egenkapitalen? Jo, egenkapitalen vokser hvis vi får et positivt resultat, og/eller hvis man får skutt inn egenkapital fra investorer.
Hvordan får vi “avgang”? Jo, egenkapitalen vil krympe hvis selskapet gir ut utbytte til eierne, eller ved underskudd i driften. Derfor blir sammenhengen slik:

IB EK + resultat + innskutt egenkapital – avsatt utbytte = UB EK

Løs denne ligningen med hensyn på avsatt utbytte.

Oppgaven sier ikke noe om innskutt egenkapital, så denne antar vi at er 0.

Spørsmål 2

Beregn egenkapitalprosenten per 31.12.2015. Oppgi svaret i % (kun tallet) med to desimalers nøyaktighet. Bruk komma som desimaltegn.

Egenkapitalprosenten (også kalt egenkapitalandelen) viser hvor stor del av samlet kapital i bedriften som er egenkapital, altså hvor stor prosent av eiendelen som er finansiert med egne midler. Med andre ord viser dette hvor mye bedriften kan tape før det begynner å gå på bekostning av de vi har lånt penger av. Dette nøkkeltallet sier noe om bedriftens soliditet. Soliditeten til en bedrift forteller oss noe om hvor stor evne bedriften har til å tåle tap. Jo større prosent, desto mer solid er bedriften.

Formelen er slik:
Egenkapitalprosent = egenkapital / totalkapital

Totalkapitalen er, som jeg gjentar til det kjedsommelige, summen av dine eiendeler (aktiva) eller summen av din egenkapital og gjeld (passiva). De skal være like store, jfr. balansen. Ettersom det er 2015 vi skal regne ut, bruker vi tallene fra 2015 🙂

Spørsmål 3

Bedriften solgte i 2015 brukte anleggsmidler for kr 1 000 000 inkl. mva. Samme år kjøpte bedriften anleggsmidler for kr 28 000 000 inkl. mva. Hvor store var bedriftens avskrivninger i 2015? Oppgi svaret i kroner (kun tallet), og bruk punktum som tusenskiller.

Vi bruker sammenhengen vår igjen.

IB + tilkomst – avgang = UB

Hva er tilkomst for anleggsmidler? Jo, det er kjøp. Kjøp av anleggsmidler gjør jo at balanseposten til anleggsmidler blir større. I dette faget er det bare kjøp som gjør at vi får høyere verdi på anleggsmidlene våre. Dessuten, legg merke til i oppgaveteksten at du har en gevinst ved salg på 96.000. Dette betyr egentlig at du selger AM til salgspris 800.000 (1.000.000 eks mva, fordi mva er jo ikke en del av balanseposten til AM) som i dine papirer er verdt 96.000 mindre: (800.000 – 96.000). Se for deg at i regnskapet ditt har du ett anleggsmiddel verdt 100.000 kroner. Det vil med andre ord si at den regnskapsmessige verdien er 100.000. Det at den regnskapsmessige verdien er 100.000 er et resultat av hvordan du har valgt å avskrive (eventuelt nedskrive) anleggsmidlet. Så skal du selge rubbel og bit. Hvis markedet da er villig til å betale 120.000, så kvitter du deg jo ikke med anleggsmidler for 120.000. Du reduserer fremdeles bare balanseposten med 100.000, hvis ikke hadde det jo stått minus i balanseposten, og det går jo ikke. Grunnen til at markedet vil betale mer enn den regnskapsmessige verdien kan f.eks. være at du har avskrevet anleggsmidlet lineært, men brukt det veldig lite eller veldig forsiktig.
Hvis du syns dette blir for komplisert: les det igjen. Syns du fremdeles det er for komplisert: se på gevinsten som en tilkomst.

Hva er avgang for anleggsmidler? Jo, det er først og fremst salg og avskrivning. Salg gjør jo at verdien på våre anleggsmidler blir lavere. Avskrivning er en planlagt kostnadsføring på anleggsmidler, som gjør at de taper verdi. Eventuelt har dere også nedskriving (men jeg vet ikke om dere har det som pensum.). Nedskrivning er en uforutsett nedjustering av verdien til anleggsmidler. F.eks dersom du eier en eiendom til 10.000.000, og eiendomsmarkedet kollapser, slik at eiendommen plutselig bare er verdt 4.000.000. Da må du nedskrive slik at regnskapet ditt gir et så riktig bilde på selskapets tilstand som mulig.

Så, med denne informasjonen skal du klare å sette opp følgende:

IB + kjøp – (salgssum fratrukket gevinst) – avskrivning – nedskrivning = UB

Løs ligningen med hensyn på avskrivninger. Husk å fjerne mva fra kjøp og salg, da de ikke har innvirkning på balanseposten til AM.

Frustrert BI-student: “JAMEN FAEN DA, DET STÅR JO IKKE NOE OM NEDSKRIVNINGER!!!!!”
Svar fra meg: “neivei, da er det vel nedskrivningene null da… Chill”

Spørsmål 4

Det var per 31.12.2014 skjulte reserver i eiendelene for kr 4 600 000. Per 31.12.2015 utgjorde skjulte reserver i eiendelene kr 4 200 000. Hva var korrekt beløp for driftsresultat i 2015? Oppgi svaret i kroner (kun tallet), og bruk punktum som tusenskiller.

De oppgavene dere får er ofte sammensatt av informasjon om skjulte reserver over x antall år, og viser hvordan den skjulte reserven øker, synker eller forholder seg lik over tid. Det som er viktig å merke seg da er at hvis en skjult reserve forholder seg uendret fra et år til et annet, vil ikke dette påvirke resultatet. Dette fordi økningen av egenkapitalen er like stor ved inngangen som utgangen av året. Hvis vi ser en reduksjon i skjulte reserver (som i vår oppgave, fra 4,6 mill til 4,2 mill) vil det reelle resultatet være dårligere enn det fremstår. Hvis vi ser en økning i skjulte reserver er det reelle resultatet bedre enn det som fremstår i regnskapet.

Så, det var teorien. Hvordan skal vi løse slike oppgaver? Jo, det finnes en veldig enkel fasit, og den er som følger (VIKTIG, kommer ofte på eksamen!):

Skjulte reserver UB 2014 = 4.600.000
Skuljte reserver UB 2015 = 4.200.000
Endring skjulte reserver = 400.000 (reduksjon)

Bokført driftsresultat 2015= ???
Endring i skjulte reserver = ???
Virkelig driftsresultat 2015 = ???

Spørsmål 5

Beregn arbeidskapitalen per 31.12.2015. Oppgi svaret i kroner (kun tallet), og bruk punktum som tusenskiller.

Arbeidskapitalen er en viktig størrelse i regnskapet, og brukes ofte til å analysere likviditeten til en bedrift. Dette er kapital som en bedrift behøver for å finansiere varer og tjenester i arbeid inntil de er solgt og oppgjøret er på konto.

Formelen er slik:

Arbeidskapital = omløpsmidler – kortsiktig gjeld

Det vi kan lese ut fra denne sammenhengen er at hvis arbeidskapitalen er positiv (>0), er deler av omløpsmidlene finansiert av langsiktig gjeld eller EK. Dersom den er negativ (<0) er noe av anleggsmidlene finansiert av kortsiktig gjeld. En gylden regel er at de AM ikke skal være finansiert av KG. Er den det, og arbeidskapitalen følgelig negativ, er som regel likviditeten til bedriften også dårlig, og de vil ha problemer med å betale sine forpliktelser i tide.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Spørsmål 6

Beregn totalkapitalens rentabilitet før skatt for 2015. Oppgi svaret i % (kun tallet) med to desimalers nøyaktighet.

Totalkapitalrentabiliteten beregnes slik:

(Driftsresultat + finansinntekter) / gjennomsnittlig totalkapital

Når det gjelder gjennomsnittlig totalkapital så finner du denne ved å ta totalkapitalen fra fjoråret (IB) pluss totalkapitalen fra dette året (UB) og dele det på to. Totalkapitalen er sum eiendeler (aktiva) eller sum egenkapital og gjeld (passiva). Disse vet vi (jfr. balansen) at er det samme. For denne bedriften er IB totalkapital 90.000.000 og UB totalkapital…?

Nå er det bare å regne ut på kalkulatoren, så finner du svaret.

Når du ser på svaret, tenker du kanskje “er dette bra eller dårlig”?. Vel, det kommer blant annet an på hvor stor risiko virksomheten representerer, men den bør jo absolutt være høyere enn lånerenten. Altså bør vi for hver krone vi låner, tjene mer enn én krone.

Gjennomsnittlig totalkapitalrentabilitet for norske bedrifter i 2011 var 9,2%

Vil du dufte av selvtillit og suksess på eksamen?

Finn din nye duft hos

Spørsmål 7

Tønsberg Mekaniske Verksted AS har noe brukt produksjonsutstyr som ikke har vært benyttet i produksjonen det siste året. Utstyret ble opprinnelig kjøpt inn for kr 400.000. Utstyret står i dag bokført i regnskapet med kr 125.000. Antatt salgsverdi er kr 100.000. Bedriften vurderer å bruke utstyret i et nytt investeringsprosjekt.

Hvilken verdi skal settes på det brukte produksjonsutstyret i investeringsbudsjettet for det nye prosjektet? Oppgi svaret (kun tallet) i kroner uten desimaler og bruk punktum som tusenskiller.

Kjære venner. Dette er en litt lang tekst, men vær vennlig å svar på den. Den er gjennomlest og gitt tommel opp fra foreleser.

Det er på tide å introdusere begrepet “alternativkostnad”. Økonomi er i stor grad studiet om hvordan vi best skal anvende knappe ressurser. Hvis vi har 100 arbeidstimer, ønsker vi å maksimere nytten av de arbeidstimene. Hvis vi har 2.000.000 kroner, ønsker vi å forvalte dem på den best mulig måten for å oppnå en så god avkastning (målt i penger eller velferd/nytte) som mulig. Når vi bruker de 100 arbeidstimene på å bygge et hus, kan vi ikke bruke de samme timene på å bygge en hytte. Gevinsten med hyttebyggingen vi må tilsidesette er alternativkostnaden ved å bygge hus.

Enda et eksempel: Alternativkostnaden min ved å gifte meg med Katharina er at jeg ikke kan gifte meg med Sarah. Jeg vil derfor kreve at Katharina blir en bedre kone enn Sarah, hvis ikke er alternativkostnaden større enn gevinsten min – og da vil jeg velge det andre alternativet, altså Sarah.

Alternativkostnad kan defineres som den gevinsten vi går glipp av ved at vi fortrenger den beste alternative anvendelsen av den knappe ressursen. Med andre ord: tapet av den beste inntekt eller fortjeneste man kunne fått dersom ressursen hadde vært plassert i en alternativ aktivitet. Eller med enda flere ord: alternativkostnaden viser verdien av den beste alternative anvendelsen av en ressurs. Der satt den tenker jeg 😉

Det finnes nesten like mange definisjoner av alternativkostnad som det finnes økonomi-forelesere her i verden, og nettet florerer med feilaktige definisjoner og forklaringer på begrepet alternativkostnad. Noen sier at alternativkostnaden er differansen mellom den dårligste og den beste av de to beste alternativene. Dette stemmer ikke. Alternativkostnaden er verdien av den gevinsten du setter til side ved å velge et alternativ. Ikke differansen mellom de to gevinstene. For å illustrere det jeg sier:

Jeg er en veldig show type. Jeg blir derfor hyret inn som konferansier til et show på Trondheim Torg. Honoraret er 40.000 kroner. Samme dag har jeg en forespørsel fra administrasjonen ved BI Trondheim om å underholde på et kurs de skal ha. Honoraret der er 10.000 kroner. Da sier altså noen at alternativkostnaden er 10.000 – 40.000. Dette er feil. Alternativkostnaden ved å velge Trondheim Torg-oppdraget er 10.000 kroner. Alternativkostnaden ved å velge BI Trondheim er 40.000 kroner.

Når vi setter opp et budsjett er det som regel grei skuring å plotte inn de kontantstrømmene som vi ser at direkte medgår i prosjektet. Men vi må også medregne de indirekte virkningene. Kanskje et prosjekt tar beslag på knappe ressurser i bedriften, som kunne blitt brukt til å skape en kontantstrøm i et annet prosjekt. Reduksjonen i kontantstrøm i det andre prosjektet må derfor også regnes med som en alternativkostnad i kontantstrømmen til det nye prosjektet. Det samme gjelder dersom vi skal produsere et nytt produkt, som kan dekke samme behov som et annet produkt vi fører. Da må vi regne med reduksjonen i kontantstrøm på det andre produktet som en alternativkostnad i kontantstrømmen til vårt nye produkt.

Så til oppgaven:

For å komme litt nærmere oppgaven, kan alternativkostnad også illustreres slik: Hvis vi antar at bedriften vår eier et anleggsmiddel til en bokført verdi på 1.500.000 og en markedsverdi (salgsverdi) på 1.000.000 kroner. Vi antar videre at dersom vi bruker anleggsmiddelet i en periode til, vil det være utdatert og derfor vil det ikke kunne selges. Ved videre bruk ofrer vi med andre ord en innbetaling på 1.000.000 kroner. Det er en alternativkostnad vi må medregne. Vi kan derfor konkludere med at gevinsten ved videre bruk, må være minst like bra som det vi kunne fått ved å selge den, sant?

Det jeg prøver å si er: i disse oppgavene må vi se på hva som er relevant for oss. Hva det ble kjøpt inn for (400.000) er ikke relevant for oss. Det er sunk cost*, altså en kostnad vi ikke kan reversere. Hvis vi ikke benytter utstyret i prosjektet er beste alternativ å selge det. Bokført verdi er den verdien utstyret er verdt i våre papirer. Dersom vi benytter det, går vi glipp av 100.000 som vi kunne solgt det for. 100.000 er altså alternativkostnaden ved å benytte utstyret i prosjektet. Hva tror du er riktig verdi å bruke i investeringsbudsjettet?

*Sunk cost. Enkelt sagt: gjort er gjort, spist er spist. Sunk cost er kostnader som påløper eller er påløpt uavhengig av om et prosjekt realiseres eller ikke, og er i så måte ikke beslutningsrelevante.
F.eks. hvis jeg kjøper en ikke-refunderbar billett til London for å shoppe, men like før jeg skal til å reise går jeg på en smell, og bruker opp alle sparepengene mine på å prøve å imponere damer på The Mint (utested i Trondheim red. anm), og ser at jeg ikke kommer til å ha så mye penger å bruke på shopping lengre. La oss nå si at en av de søteste jentene fra kvelden på The Mint ringer meg, og inviterer meg på romantisk telttur i Bymarka. Hva skal jeg gjøre? Skal jeg reise til London? Jeg har ingenting å gjøre i London uten penger, og jeg bør jo prioritere teltturen med drømmejenta? Men på den annen side har jeg jo betalt billetten, så hvis jeg ikke reiser er det jo å kaste penger ut av vinduet? Nei, skal vi tenke bedriftsøkonomisk på det, skal vi anse billetten som sunk cost, og den skal derfor ikke medregnes når jeg skal ta min beslutning. Det er med andre ord lite rasjonelt av meg å reise til London uten å ha noe der å gjøre, så jeg blir med på telttur.

Spørsmål 8

Industribedriften Fjorden AS har følgende sammenheng mellom kostnader i millioner kroner og produksjonsmengde i antall enheter:

Produksjonsmengde	0	1000	2000	3000	4000	5000	6000
Kostnader	8	9	10	11	12	13	14

Hvor store er bedriftens faste kostnader? Oppgi svaret( kun tallet) i millioner kroner

Dere har nå altså begynt å jobbe med det som heter variable og faste kostnader. Det er egentlig veldig, veldig enkelt.
De variable kostnadene er de kostnadene som varierer med hvor mange varer du produserer. Hvis du er en baker, vil de variable kostnadene være det du putter i kaka. For vi kan være enige om at antall kg mel og sukker vil variere med antall kaker du baker, sant? I dette faget tar vi forutsetning om at vi har “proporsjonale variable kostnader”. Det betyr i all enkelhet at vi forutsetter at vi bruker like mye mel og sukker i den første kaka, som i den andre, tredje, fjerde osv. En annen kostnad som er variabel er lønn. Vi skjønner jo at hvis en person skal bake 1 kake, eller om en person skal bake 5 kaker, så er tiden (og dermed lønnskostnaden) variabel. Vi forutsetter også her at lønnskostnadene er proporsjonale.
I motsetning til de variable kostnadene, er de faste kostnadene like store uansett hvor mange enheter du produserer (det er egentlig ikke sant, men i dette faget forutsetter vi det). Det kan vi illustrere ved at bakeriet ditt har en fast husleie. Du betaler 6.000 i mnd i husleie. I tillegg har du en stekeovn og diverse annet bakeutstyr, du leaser for 1.000 kroner i mnd. Da blir din faste kostnad 7.000 kroner i mnd. Den vil være 7.000 uansett om du produserer én kake eller 1.000 kaker.

Hvis vi da ser på tabellen over, ser du at hvis du produserer 0 enheter, er de totale kostnadene dine (faste kostnader + variable kostnader) 8 (millioner). Hvis du produserer 1.000 enheter er kostnadene dine 9. Hva er de faste kostnadene?

Spørsmål 9

Industribedriften Fjorden AS har følgende sammenheng mellom kostnader i millioner kroner og produksjonsmengde i antall enheter:

Produksjonsmengde	0	1000	2000	3000	4000	5000	6000
Kostnader	8	9	10	11	12	13	14

Hvor store er bedriftens variable kostnader når produksjonsmengden er 3.000 enheter? Angi svaret (kun tallet) i millioner kroner uten desimaler.

Se forklaring på oppgave 8

Spørsmål 10

En restaurant kjøpte i en gitt periode inn råvarer for kr 44.000. Det var råvarer på lager ved periodens begynnelse for kr 7.000. Beholdningen av råvarer ved periodens slutt var kr 5.000. Hva var restaurantens råvarekostnad i perioden? Oppgi svaret (kun tallet) i hele kroner og bruk punktum som tusenskiller.

Denne ligningen bør du kunne nå. Hvis ikke er sammenhengen:

IB + tilkomst – avgang = UB
mao: IB + kjøp – forbruk = UB
Løs med hensyn på forbruk, så har du svaret.

Posted on 19.02.201919.04.2022

Bedriftsøkonomi og finans – arbeidskrav 4 (2019)

Vi tar utgangspunkt i følgende tall til de neste oppgavene:

Du får oppgitt følgende nøkkeltall fra en bedrifts årsregnskap for 2015:

Spar stort: Kjøkkenutstyret du kupper på tilbud nå

Totalkapitalens rentabilitet = 12%

Egenkapitalens rentabilitet = 20%

Resultatgraden = 15%

Likviditetsgrad 1 per 31.12. 2015 = 1,5

Egenkapitalprosenten per 31.12.2015 = 30%

Anleggsmidler per 31.12.2015 = kr 6.000.000 (Per 01.01.2015 = kr 5.000.000)

Omløpsmidler per 31.12.2015= kr 4.000.000 (Per 01.01.2015 = kr 3.000.000)

Oppgave 1

Hvor stor er egenkapitalen per 31.12.2015? Oppgi svaret i kroner (kun tallet), og bruk punktum som tusenskiller.

Disse oppgavene vipper folk lett av pinnen, og første gang de ble presentert på eksamen var eksamenssalene rundt om i landet preget av gråt, sinne, frustrasjon og hodekløing. Mange leverte blankt, og forlot eksamen etter 1 time. Dette er det jeg ønsker at ikke skal skje hvis dere kommer i en situasjon hvor dere får en oppgave som ikke er blitt gitt på eksamen før. Dere går på en høyskole, og skal inneha viktige roller i næringslivet i årene fremover – så det er viktig at vi har litt kunnskap om det vi regner på, og ikke bare memorerer gamle eksamensoppgaver.

Det vi skal gjøre i de kommende oppgavene er å snu og vende på formler. Og igjen, vær så snill å pugg (og forstå) formlene i dette kapittelet. Det er ingen vei utenom, som vi skal se på i dette arbeidskravet. Jeg elsker disse oppgavene, fordi du får en litt mer helhetlig forståelse av det man driver med.

BTW: noen har spurt meg om å lage et formelark i faget. Det kunne jeg gjort, men jeg vil at dere skal gjøre det selv. For det jeg anbefaler dere å gjøre er å bla gjennom boka, skriv ned og systematiser formlene selv. Da lærer dere mye! 🙂

Så, til oppgaven:

Her blir vi spurt om hva egenkapitalen er ved utgangen av 2015. Her har vi fått oppgitt egenkapitalprosenten, som er 30%. Formelen for egenkapitalprosent er som følger.

Egenkapitalprosent = egenkapital / totalkapital

Som vi har sett før kan vi ofte løse slike oppgaver ved å se på formlene som ligninger. Det som er viktig da er at vi husker formlene. Overfor ser vi en formel, som i bunn og grunn er en ligning. Vi vet egenkapitalprosenten, og vi vet totalkapitalen. Totalkapitalen er som vi huser summen av våre aktiva (eiendeler) eller summen av våre passiva (egenkapital og gjeld). Her har vi fått oppgitt at våre AM og våre OM til sammen utgjør 10.000.000. Altså er vår totalkapital 10.000.000. Da mine venner, har vi en ligning med én ukjent, og det skal du kunne klare å løse.

Oppgave 2

Hvor stor er samlet gjeld per 31.12.2015? Oppgi svaret i kroner (kun tallet), og bruk punktum som tusenskiller.

Vi vet at gjelden vår består av kortsiktig og langsiktig gjeld (jfr balanseligningen). Vi vet at
AM + OM = EK + LG + KG

Hvis vi da skriver
AM + OM = EK + gjeld

Du har AM, OM og EK (hvis du har klart oppgave 1), og vil finne gjelden. Ligning med én ukjent. Vær så god, kjør på 🙂

Oppgave 3

Hvor stor er kortsiktig gjeld per 31.12.2015? Oppgi svaret i hele kroner (kun tallet), og bruk punktum som tusenskiller.

Ja, hvordan i huleste Sabeltann skal vi finne ut dette da? Joda, ta en slurk kaffe, og tenk på hva vi har fått oppgitt. Kan vi tenke oss en formel som kan gi oss en ligning med én ukjent? Ja, det kan vi. Vi har f.eks. formelen for likviditetsgrad 1. Likviditetsgrad 1 er jo et tall som viser forholdet mellom våre omløpsmidler og vår kortsiktige gjeld. Den er som følger:

L1 = OM/KG

Vi har L1 (=1,5), og OM. Da skal du finne KG ved hjelp av enkel matematikk! 🙂

Oppgave 4

Hvor store var bedriftens salgsinntekter i 2015? Oppgi svaret i kroner (kun tallet) og bruk punktum som tusenskiller.

Hei, og velkommen til spørsmål 4. Din frustrasjon er registrert.
La oss igjen ta en slurk kaffe, eller nypete (nyper inneholder masse C-vitamin, noe du trenger når du er offer for stress), og se hva vi har å jobbe med.

Igjen, prøv å finn en formel du kan, som inneholder det du leter etter. Jeg tenker at formelen for kapitalens omløpshastighet kan funke:

Kapitalens omløpshastighet = salgsinntekt/gjennomsnittlig totalkapital

Denne kan du naturligvis snu på, slik at den blir slik:

Salgsinntekt = Gjennomsnittlig totalkapital * kapitalens omløpshastighet

Her har du imidlertid en ligning med TO ukjente (omløpshastigheten og salgsinntekt), så vi må finne én av dem.
I forrige arbeidskrav så vi på DuPont-modellen, som forteller oss at:

TKR = resultatgrad * kapitalens omløpshastighet

Hvis vi snur på denne får vi at:

Kapitalens omløpshastighet = TKR/resultatgrad

TKR (Totalkapitalens rentabilitet) har vi fått oppgitt. Resultatgraden har vi fått oppgitt. Finn kapitalens omløpshastighet, sett den inn i den første ligningen, og løs 🙂

Hvis det er noen trøst, dette er nok den vanskeligste oppgaven du kan få på eksamen (i dette temaet, hehe).

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Oppgave 5

En bedrift betalte kr 272.500 inkl. mva i diverse driftskostnader i 2015. Per 1.1.2015 hadde bedriften ubetalte driftskostnader ekskl. mva fra 2014 for kr 12.000. En gjennomgang av regnskapet per 31.12.215 viste at av betalte driftskostnader i 2015 var kr 15.000 ekskl. mva forskuddsbetaling for 2016. Hva ble resultatført som driftskostnader i resultatregnskapet i 2015? Oppgi beløpet i hele kroner (kun tallet), og bruk punktum som tusenskiller.

Dette mine markedsførere, er periodisering i sin enkleste form!

Du har betalt 272.500 inkl mva i 2015. Ved inngangen av året hadde du 12.000 ekskl. mva som tilhører 2014, men som inngår i de 272.500 du betalte i 2015. De skal likevel ikke føres i 2015, men altså i 2014. Ved utgangen av 2015 viste det seg at i de 272.500 du betalte i 2015 tilhørte 15.000 ekskl. mva 2016.

Riktig måte å sette opp dette på eksamen blir altså:

Totale diverse betalte driftskostnader (OBS: EKS. MVA!)
+/- 12.000 ubetalt fra 2014
+/- 15.000 forskudd for 2016

Hva som er pluss eller minus må du tenke deg til selv.

Dette blir et veldig enkelt regnestykke. Lykke til.

Oppgave 6

En bedrift regnskapsfører kr 80.000 inkl. mva som tap på fordringer. Hvilke regnskapsmessige virkninger har transaksjonen? Oppgi bokstaven for det svaralternativet nedenfor som du mener er korrekt.

a. Ordinært resultat før skatt reduseres med kr 64.000, skyldig mva (netto) reduseres med kr 16.000 og omløpsmidler reduseres med kr 80. 000.

b. Ordinært resultat før skatt reduseres med kr 80.000, skyldig mva (netto) reduseres med kr 20.000 og omløpsmidler reduseres med kr 60. 000.

c. Ordinært resultat før skatt reduseres med kr 60.000, skyldig mva (netto) reduseres med kr 16.000 og omløpsmidler reduseres med kr 80. 000.

d. Ordinært resultat før skatt reduseres med kr 80.000, skyldig mva (netto) reduseres med kr 16.000 og omløpsmidler reduseres med kr 64.000.

e. Ordinært resultat før skatt reduseres med kr 60.000, skyldig mva (netto) reduseres med kr 20.000 og omløpsmidler reduseres med kr 80. 000.

f. Ordinært resultat før skatt reduseres med kr 64.000, skyldig mva (netto) reduseres med kr 16.000 og omløpsmidler reduseres med kr med kr 64.000.

Skal vi bare eliminere?
Husker du balanseligningen?

AM + OM = EK + LG + KG

En kundefordring (faktura) står på OM, fordi det vanligvis (dog ikke i dette tilfellet, haha) blir omgjort til penger ila kort tid. Denne kundefordringen står som 80.000, og er inkludert mva – fordi det er det som står på fakturaen til kunden.
La oss bare fjerne denne momsen først som sist. Da ganger vi med 0,20 (ikke 0,25, se eget innlegg om mva-regning hvis du lurer på hvorfor)

80.000*0,20 = 16.000. 16.000 er altså mva-beløpet (ikke beløpet eks. mva)
80.000 – 16.000 = beløp eks. mva = 64.000 (64.000 kunne du også kommet frem til ved å ta 80.000/1,25)

Da vi i god tro sendte ut denne fakturaen til vår uærlige eller konkurstruede kunde, gjorde vår sexy regnskapsfører følgende endring i balansen vår:

AM:
OM: +80.000 (kundefordring)
=
EK: +64.000 (resultat)
LG
KG: +16.000 (skyldig moms til staten)

Nå gikk det dessverre ikke slik, så vår hardtarbeidende regnskapsfører må trå til igjen, og reversere dette. Hva gjør hun (eller han…?) da, og hvilket svaralternativ blir rett?

Oppgave 7

En bedrift benytter lineære avskrivninger for sine maskiner. Avskrivningssatsen er 25 %. Maskinene ble kjøpt inn ved inngangen til året 20×1 for kr 2.000.000 eksklusive mva. Restverdi ved utløpet av levetiden ble anslått til kr 200.000 eksklusive mva. Etter tre år ble maskinen solgt. Gevinsten ved salget var kr 18.000. Hva var salgssummen eksklusive mva? Oppgi salgssummen (kun tallet) i hele kroner og bruk punktum som tusenskiller.

Her har vi lineære avskrivinger, men med en avskrivingssats på 25%. Dette kan virke forvirrende, siden vi har en prosentsats OG beskjed om å bruke lineær metode. Dette er egentlig bare en måte å si at du skal avskrive over 4 år. Lineær avskrivingsmetode betyr jo at avskrivingen skal være den samme hvert år. Ettersom vi også får oppgitt at avskrivingssatsen er 25%, må det bety at de beregner levetiden (brukstiden) til å være 4 år. Hadde satsen vært 20% hadde de beregnet levetiden (brukstiden) å være 5 år. 10%, 10 år, osv osv.

Twisten i denne oppgaven er at de ikke hadde den hele den planlagte levetiden. De solgte den etter 3 år. Da må finne ut hva maskinene var verdt etter tre år. I tillegg får du informasjon om at de solgte den med en gevinst (altså fikk de 18.000 mer enn den egentlige verdien)

Finn akkumulerte avskrivinger for de 3 årene (altså den samlede avskrivingen etter 3 år), og pluss på 18.000, så har du nok svaret. Det fikk i hvertfall jeg.

Vi tar utgangspunkt i følgende tall til de neste oppgavene
Nedenfor er vist et resultatbudsjett og balansebudsjett for bedriften Trollgard AS for året 20×1. Bedriften driver en mva-pliktig virksomhet. Mva-satsen er 25%.

Resultatbudsjett for året	20×1
Driftsinntekter	80.000
Driftskostnader	59.000
Driftsresultat	21.000
Renteinntekter	300
Rentekostnader	1.300
Resultat før skattekostnad	20.000
Skattekostnad	5.400
Årsresultat	14.600

Balanse per 31.12.	20×1	20×0
Anleggsmidler	76.000	65.000
Omløpsmidler	34.000	25.000
Sum eiendeler	110.000	90.000

Egenkapital	41.000	30.000
Langsiktig gjeld	36.000	34.000
Kortsiktig gjeld	33.000	26.000
Sum egenkapital og gjeld	110.000	90.000

Tilleggsopplysninger:

Varelager 6.000 4.000

Kundefordringer 8.000 11.000

Leverandørgjeld 10.000 14.000

Varekostnad 30.000

Avskrivninger 10.000

Alt varekjøp og varesalg skjer på kreditt.

Oppgave 8

Beregn budsjetterte utbetalinger til leverandørene i 20×1. Oppgi svaret (kun tallet) i hele kroner , og bruk punktum som tusenskiller.

Jeg har tidligere skrevet om den generelle ligningen for balanseberegninger: IB + tilkomst – avgang = UB. Denne kan vi bruke også her:

Anslått IB leverandørgjeld +budsjettert innkjøp (inkl. mva) – Utbetalinger til leverandørene = budsjettert UB leverandørgjeld

Denne snur vi på, slik som andre ligninger, og får følgende oppsett

Anslått IB leverandørgjeld
+ Budsjettert innkjøp (inkl. mva)
– budsjettert UB leverandørgjeld
= periodens budsjetterte utbetalinger til leverandører

Varekjøpet husker vi at vi finner ved å snu og vende på lagerligninga: Husk at vareforbruk er det samme som varekostnad (fordi, vi husker jo at en kostnad oppstår når vi forbruker).

Vareforbruk = IB varelager + Varekjøp – UB varelager
Altså:
Varekjøp = Vareforbruk – IB varelager + UB varelager

Husk at varekjøpet skal være inkl mva! Grunnen til dette skal jeg forklare kort:
I balansen er de alle verdiene oppgitt uten mva, med to unntak: leverandørgjeld og kundefordringer (som jo egentlig er to sider av samme sak. Vår leverandørgjeld er jo leverandørene sin kundefordring, og våre kundefordringer er våre kunders leverandørgjeld). Leverandørgjelda vår er jo det beløpet som står på regninga.

Så når vi skal regne ut hva forventet utbetaling til leverandørene er, må vi regne med mva på innkjøpet. Hvorfor? Fordi det vi betaler ut til leverandøren er jo inkludert mva, fordi beløpet på regninga er inkludert mva. Hvis vi ikke inkluderer mva blir ikke ligninga konsistent.

Da er det bare å regne da 🙂

Oppgave 9

Hva planlegger bedriften å ta opp som nye langsiktige lån i 20×1? Oppgi svaret i hele kr, og bruk punktum som tusenskiller.

Dette er i grunn relativt simpel regning. Du må bare se sammenhengen i ting. Teksten sier “posten langsiktig gjeld i balansen inneholder flere langsiktige lån med ulik løpetid. I 20×1 skal bedriften betale avdrag med kr 2.000.” Det betyr altså at det du tenker å ta opp i nye lån er differansen mellom det du har når du går ut av året + avdraget du har tatt minus det du hadde da du startet. Eksempelvis, dersom du har 1000 kroner i kredittkortgjeld 1. januar, og 2000 kroner i kredittkortgjeld 31. desember samme år, og du har betalt inn 500 kroner ila året, betyr det at du har tatt opp 1.500 i kredittkortgjeld ila året.

Igjen bruker vi ligninga vår. Denne gang med hensyn på langsiktig gjeld:
Anslått IB langsiktig gjeld – budsjetterte avdrag + budsjettert nye langsiktige lån = UB langsiktig gjeld

Løs ligningen, så finner du svaret.

Oppgave 10

Beregn budsjetterte innbetalinger fra kundene i 20×1. Oppgi svaret (kun tallet) i kroner, og bruk punktum som tusenskiller.

Anslått IB kundefordring + budsjettert salgsinntekt (inkl mva) – innbetaling fra kunder = UB kundefordring
Denne har vi ingen problemer med å snu på, slik vi gjorde i oppgave 8. Gjør det, og sett den opp slik du ville gjort for sensor.

Her er det viktig å merke seg tilleggsinformasjonen i oppgaven. Nemlig at vi har et tap på fordring på 800 kroner. Denne “knipa” løser du enkelt ved å fjerne 800 + mva. fra det opprinnelige svaret ditt. Hvorfor legge til mva? Jo fordi, som jeg skrev tidligere, kundefordringene er bokført inkludert mva i balansen, så når kundefordringen slettes (tapsføres) blir hele beløpet slettet fra balansen.

Nå er du i mål med denne ukes arbeidskrav. Gratulerer.

Posted on 12.02.201919.04.2022

Bedriftsøkonomi og finans – arbeidskrav 3 (2019)

Vi tar utgangspunkt i disse tallene:

1. Hva var totalkapitalens rentabilitet før skatt for Tuscon Subsea AS i 20×1? Oppgi svaret (kun tallet) i hele prosent (avrund hvis nødvendig).

Totalkapitalrentabiliteten beregnes slik:

(Driftsresultat + finansinntekter) / gjennomsnittlig totalkapital

Nå er det bare å regne ut på kalkulatoren, så finner du svaret.

Gjennomsnittlig totalkapitalrentabilitet for norske bedrifter i 2011 var 9,2%

2. Hva var egenkapitalens rentabilitet før skatt for Tuscon Subsea AS i 20×1? Oppgi svaret (kun tallet) i hele prosent (avrund hvis nødvendig).

Da vi regnet ut totalkapitalrentabiliteten (TKR) så vi hvordan den samlede kapitalen til bedriften forrentet seg. Nå skal vi se på egenkapitalens rentabilitet (EKR), som er veldig interessant for eierne og potensielle eiere av bedriften. Den viser hvordan eiernes investerte kapital utvikler seg. Dersom man står overfor en bedrift som er 100% finansiert av egenkapital (ingen gjeld), vil totalkapitalrentabiliteten og egenkapitalrentabiliteten være like stor. (Det er klare sammenhenger mellom EKR og TKR, og denne kan blant annet illustreres gjennom brekkstangformelen.) For deg som skal investere penger vil det kanskje være interessant å se hvilke av bedriftene du skal investere i som har høyest egenkapitalrentabilitet. Det som er viktig å huske er at eierne kommer sist når kapitalen skal fordeles. Først skal vareleverandørene, arbeidstakere, bankene osv. ha sine penger. Deretter, hvis det er noe til overs, går det til egenkapitalen.

ordinært resultat før skatt / gjennomsnittlig egenkapital

Gjennomsnittlig egenkapital får du ved å ta IB egenkapital + UB egenkapital og dele det på 2. UB egenkapital i våre tall er 42.984, og IB egenkapital er…?

3. Hvor mye ble avsatt til utbytte per 31.12.20×1? Oppgi svaret i hele tusen kroner (kun tallet), og bruk punktum som tusenskiller.

Hvis dere ikke har lært dere denne sammenhengen, så kan det hende dere syns BØK er litt håpløst. Denne ligninga får ofte mye til å løsne i dette faget:

IB + tilkomst – avgang = UB

For den som trenger å få det inn med teskje. Det denne ligninga sier er:
Så mye hadde jeg (IB) + så mye fikk jeg (tilkomst) – så mye ga jeg bort (avgang) = så mye har jeg igjen (UB).

Tilkomst er det som gjør at beholdningen/balanseposten blir større.
Avgang er det man kvitter seg med, og som følgelig gjør at beholdningen eller balanseposten blir mindre.

Denne kan også brukes her, og da må vi spørre oss selv, hva er “tilkomsten” og “avgangen” her?

IB EK + resultat + innskutt egenkapital – avsatt utbytte = UB EK

Løs denne ligningen med hensyn på avsatt utbytte.

Oppgaven sier ikke noe om innskutt egenkapital, så denne antar vi at er 0!

————-

Vi skal nå foreta ett ledd i det som kalles en likviditetsanalyse. Det er en analyse av betalingsevnen til en bedrift, altså bedriftens evne til å betale sine regninger i tide. Så vidt jeg kan se, skal dere ta for dere følgende “direkte” måter å beregne likviditeten til en bedrift på:
– Likviditetsgrad 1 (bør være større enn 2)
– Likviditetsgrad 2 (bør være større enn 1)
– Arbeidskapital

Det er viktig å presisere at man ikke får et fullstendig bilde ved å foreta disse analysene, da de er basert på balansen. Som vi vet gir balansen et uttrykk for en bedrifts finansielle situasjon på et gitt tidspunkt. Det kan gi et feilaktig bilde. Ta f.eks. en titt på likviditetsgradene til en av verdens største bedrifter, Coca Cola. Er likviditeten pr. definisjon god? Kanskje ikke. Er Coca Cola på randen av konkurs? Tvilsomt.

Det er viktig å se på andre faktorer, som f.eks. kredittider på gjeld og fordringer, nedbetalingstider, ubenyttet kassakreditt osv, osv…

4. Hva var endringen i arbeidskapitalen fra 20×0 til 20×1? Oppgi svaret (kun tallet) i hele tusen kroner og bruk punktum som tusenskiller. Har arbeidskapitalen blitt redusert, skal endringen angis med negativt fortegn.

Formelen er slik:

Arbeidskapital = omløpsmidler – kortsiktig gjeld

Regn ut arbeidskapitalen for de to årene, og se hva endringen er.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

5. Beregn likviditetsgrad 1 per 31.12.20×1. Oppgi svaret (tallet) med to desimalers nøyaktighet og uten benevning. Bruk komma som desimaltegn.

Likviditetsgrad 1 er et enkelt regnestykke. Man ser på forholdet mellom omløpsmidlene (bankinnskudd, fordringer, varelager osv.) og den kortsiktige gjelden. Altså:

L1 = omløpsmidler / kortsiktig gjeld

Her skal du bruke tallene for 20X1, ikke gjennomsnittet mellom IB og UB!

Litt om likviditetsgrad 2 i tillegg:

Likviditetsgrad 2 beregnes nesten likt, men tar utgangspunkt i våre mest likvide omløpsmidler – altså de omløpsmidlene som er penger, eller fort kan gjøres om til penger (eller til “likvider” som man sier når man skal være fancy). Dette betyr for alle praktiske formål omløpsmidler minus regnskapsført verdi på varelageret vårt. Dette ser vi i forhold til kortsiktig gjeld. Altså:

L2 = (omløpsmidler – varelager) / kortsiktig gjeld

6. Beregn egenkapitalprosenten per 31.12.20×1. Oppgi svaret (kun tallet) med to desimalers nøyaktighet.
Egenkapitalprosenten (også kalt egenkapitalandelen) viser hvor stor del av samlet kapital i bedriften som er egenkapital, altså hvor stor prosent av eiendelen som er finansiert med egne midler. Med andre ord viser dette hvor mye bedriften kan tape før det begynner å gå på bekostning av de vi har lånt penger av. Dette nøkkeltallet sier noe om bedriftens soliditet. Soliditeten til en bedrift forteller oss noe om hvor stor evne bedriften har til å tåle tap. Jo større prosent, desto mer solid er bedriften.

Formelen er slik:
Egenkapitalprosent = egenkapital / totalkapital

Totalkapitalen er, som jeg gjentar til det kjedsommelige, summen av dine eiendeler (aktiva) eller summen av din egenkapital og gjeld (passiva). De skal være like store, jfr. balansen. Ettersom det er 20X1 vi skal regne ut, bruker vi tallene fra 20×1 🙂

7. Bedriften har verdsatt sitt varelager meget forsiktig. Per 31.12.20×0 utgjorde skjulte reserver kr 4 000 000. Per 31.12.20×1 utgjorde skjulte reserver kr 4 700 000. Beregn korrekt driftsresultat for 20×1. Oppgi svaret i kroner (kun tallet). Bruk punktum som tusenskiller.

De oppgavene dere får er ofte sammensatt av informasjon om skjulte reserver over x antall år, og viser hvordan den skjulte reserven øker, synker eller forholder seg lik over tid. Det som er viktig å merke seg da er at hvis en skjult reserve forholder seg uendret fra et år til et annet, vil ikke dette påvirke resultatet. Dette fordi økningen av egenkapitalen er like stor ved inngangen som utgangen av året. Hvis vi ser en reduksjon i skjulte reserver vil det reelle resultatet være dårligere enn det fremstår. Hvis vi ser en økning (slik i vår oppgave) i skjulte reserver er det reelle resultatet bedre enn det som fremstår i regnskapet.

Så, det var teorien. Hvordan skal vi løse slike oppgaver? Jo, det finnes en veldig enkel fasit, og den er som følger (VIKTIG, kommer ofte på eksamen!):

Skjulte reserver UB 20×0 = 4.000.000
Skuljte reserver UB 20×1 = 4.700.000
Endring skjulte reserver = 700.000 (økning)

Bokført driftsresultat 20×1= ???
Endring i skjulte reserver = ???
Virkelig driftsresultat 20×1 = ???

8. Du får følgende opplysninger om en bedrift:
Totalkapitalens omløpshastighet er 4.
Resultatgraden er 3%.
Gjennomsnittlig gjeldsrente er 5%.
Total gjeld utgjør 15 mill.kr.
Egenkapitalen utgjør 30 mill.kr.

Hva er egenkapitalens rentabilitet? Oppgi svaret i % (kun tallet) med en desimals nøyaktighet. Bruk komma som desimaltegn.

Denne fremstår kanskje som litt krevende, men det er ved å løse slike oppgaver at det ofte går opp et lys eller to. La oss systematisere informasjonen noe:

Altså:
-Totalkapitalens omløpshastighet er 4.
*Forteller oss at den investerte kapitalen blir omsatt 4 ganger i løpet av et år. Formelen for totalkapitalens omløpshastighet er:
salgsinntekt / gjennomsnittlig totalkapital

-Resultatgraden er 3%.
*Forteller oss hvor stor del som tilfaller selskapet av hver krone som omsettes. Mao, hvor stor lønnsomheten er i forhold til de totale inntektene.
Formelen er: ordinært resultat før skatt + rentekostnad / salgsinntekt

-Gjennomsnittlig gjeldsrente er 5%.
*Forteller oss at vi i snitt betaler 5% rente på våre lån.
Formelen for gjennomsnittlig gjeldsrente er: rentekostnad/gjennomsnittlig gjeld

-Total gjeld utgjør 15.000.000
-Egenkapitalen utgjør 30.000.000
* Summen av total gjeld og egenkapital forteller oss at totalkapitalen er på 45.000.000 kroner. Totalkapitalen er jo som kjent summen av våre eiendeler (aktiva) eller vår egenkapital og gjeld (passiva)

Når jeg da i tillegg presenterer følgende formel, som kalles brekkstangformelen (viktig å lære, kommer ofte tekstspørsmål om denne på eksamen OBSOBS! Les side 454-455 i Økonomistyring 1-boka (Sending)), så blir dette kanskje lettere enn vi hadde trodd.

Brekkstangformelen:
EKR = TKR + (TKR – GGR) * G/EK

Hvor:
EKR = egenkapitalrentabiliteten
TKR = totalkapitalrentabiliteten
GGR = gjennomsnittlig gjeldsrente
G/EK = gjeld/egenkapital

Nå har vi en ligning med to ukjente (TKR og EKR). Hvis vi da retter vårt blikk til side 450 i Sending-boka, ser vi på DuPont-modellen at totalkapitalrentabiliteten fremkommer som et produkt av kapitalens omløpshastighet og resultatgraden. Med andre ord finner vi TKR ved å ta:

Kapitalens omløpshastighet * resultatgraden = 4 * 3% = 4*0,03 = 0,12

Nå er brekkstangformelen plutselig bare med én ukjent, nemlig EKR, så da er det bare å regne ut.

9. En bedrift har anskaffet et varig driftsmiddel for kr 1.200.000 inklusive mva. Forventet levetid for driftsmiddelet er 5 år. Anslått salgsverdi ved utløpet av levetiden er kr 100.000 inklusive mva. Anta at bedriften benytter lineære avskrivninger. Hva blir avskrivningene i år tre? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

Hva er en avskriving? Det enkleste er å se på det som en slags periodisering av kostnadene knyttet til en stor investering som du “forbruker” over tid. F.eks. hvis du kjøper et anleggsmiddel i form av en maskin du skal bruke til produksjonen, er det feil å sette av hele denne utgiften i det året du kjøpte den. Du fordeler utgiften som kostnad over dens levetid.

Det finnes flere måter å beregne avskrivinger på, og det er opp til hver enkelt bedrift å avgjøre hvilken metode som er mest fornuftig for deres investeringer. De metodene vi kommer borti i dette faget er:

Lineær avskriving. Lineær avskrivingsmetode betyr at avskrivingen skal være den samme hvert år.
Saldoavskriving: Hvert enkelt år avskrives med en konstant prosentandel av det som er bokført verdi av f.eks maskinen ved årets begynnelse (01.01.XXXX). Denne metoden innebærer, i motsetning til lineær avskriving at avskrivingene vil bli lavere for hvert år, siden bokført verdi hele tiden reduseres etter hvert som driftsmiddelet avskrives.
I tillegg til disse har du også produksjonsenhetsmetoden, som tar hensyn til at driftsmidlets verdiforringelse skyldes bruken av det, og ikke så mye av “tidens tann”.

I denne oppgaven får du oppgitt at bedriften bruker lineær avskrivingsmetode. Vi får oppgitt at forventet levetid er 5 år (altså skal de fordele kostnadene over 5 år). Når de fem årene har gått, kommer den fremdeles til å ha en markedsverdi på 100.000 (80.000 eks mva) – altså er den ikke “helt oppbrukt”.

Da må du rett og slett finne ut hva den årlige avskrivingssummen er. Den er som sagt den samme hvert år når man benytter lineær avskriving.

Formelen for lineære avskrivninger er

(Anskaffelseskost – utrangeringsverdi) / forventet levetid

Husk at summene skal være eks mva. Du skal jo ikke avskrive momsen. Vil du lære mer om mva-regning, har jeg skrevet et innlegg om det her: http://hobbyokonomen.blogg.no/1442513016_17092015.html

10. En bedrift har anskaffet et varig driftsmiddel for kr 1.200.000 inklusive mva. Forventet levetid for driftsmiddelet er 5 år. Anslått salgsverdi ved utløpet av levetiden er kr 100.000 inklusive mva. Anta at bedriften benytter saldoavskrivninger. Saldoavskrivningssatsen er satt til 40%. Hva blir avskrivningene i år tre? Oppgi svaret (kun tallet) i hele kroner, og bruk punktum som tusenskiller.

Saldoavskrivingssatsene vil variere fra år til år. De vil bli mindre for hvert år, ettersom de baseres på en prosentsats av restverdien ved inngangen av året.

Generelt betyr det altså.

År 1: restverdi pr. 1.1 * saldosats = avskrivingsbeløp år 1

År 2: (restverdi år 1 – avskrivingsbeløp år 1) * saldosats.

Et eksempel med tall:

Verdi varig driftsmiddel: 1.000.000

Prosentsats: 10%

År 1: 1.000.000 * 0,10 = 100.000 <—– Avskrivingsbeløpet i år 1 er altså 100.000

År 2: (1.000.000-100.000) * 0,10 = 90.000 <——- Verdien i år 2 er 900.000, og avskrivingssummen er derfor 90.000

År 3: (900.000-90.000) * 0,10 = 81.000 <—- Avskrivingssummen i år 3 er 81.000

Nå, prøv det samme med tallene i vår oppgave. Husk at også her må du trekke fra mva. på alle verdiene

Posted on 24.01.201919.04.2022

La oss snakke litt om lån

Frem til nå har innleggene på denne bloggen utelukkende vært skrevet for økonomistudenter. Dette innlegget er også ment for den gjennomsnittlige personen som ønsker å lære mer om privatøkonomi enn det tabloidene klarer med sin overfladiske journalistikk på området. Planen min er å publisere flere slike innlegg i tiden fremover i et forsøk på å spre kunnskap om hverdagslige økonomiske temaer som er viktige for alle. Kall det gjerne mitt forsøk på samfunnsansvar. Innleggenes nivå vil ligge et sted mellom folkelig helgejournalistikk og akademiske publikasjoner. Det kan derfor virke litt for omfattende for noen, og litt for forenklet for andre.

Mine lesere er stort sett økonomistudenter, men nå har du altså muligheten til å dele meg med din kjære mor, søster og bror også.

Lån er et av de viktigste redskapene i husholdningenes finansielle verktøykasse. Likevel viser forskning at den økonomiske kunnskapen omkring gjeldsopptak er relativt begrenset blant husholdningene, og at mangelen på kunnskap fører til at låntakerne stiller svakt overfor långiver, spesielt når det gjelder valg av låneprodukter. Folks mangel på økonomisk kunnskap i tillegg til mangel på kunnskap om bankenes prosesser, samt interne og eksterne retningslinjer fører ofte til misforståelser, misnøye og for mange en følelse av urettferdighet. Hvorfor fikk venninnen min lån, og ikke jeg? Hvorfor gir DNB meg tre millioner i lån, mens Sparebank 1 bare gir meg 2,7 millioner? Hvorfor har naboen min lavere rente enn meg?

Det viktigste du skal ta med deg fra dette innlegget er ikke detaljene. De er der bare for å gi litt kjøtt på beinet. Det viktigste er at den grunnleggende forståelsen skal ligge i underbevisstheten når du tar økonomiske beslutninger.

Hvorfor låner vi?

Hvorfor låne penger? Et åpenbart svar er jo: “jeg har ikke penger akkurat nå, men vil ha den greia der akkurat nå.” Denne argumentasjonen er ganske enkel å forstå, og vi kan godt ta utgangspunkt i den – men hva er det som ligger bak? I utsagnet “vil ha” ligger det implisitt at vi kan ha en eller annen form for nytte av å ha denne gjenstanden allerede i dag, fremfor å vente med å kjøpe den til vi har penger nok. Det kan være nytte i form av økonomisk gevinst (f.eks investering i noe som gir avkastning) eller i form av bruksnytte (deilig å slippe å ta oppvasken for hånd frem til vi har spart opp penger til oppvaskmaskin).

I økonomisk teori spiller begrepet nytte en veldig sentral rolle. Jeg har ikke tenkt å fokusere mye på det i dette innlegget. For dette formålet holder det at vi forstår at nytte er et slags mål på tilfredshet, som naturligvis vil variere fra person til person. I økonomisk teori sier vi at man har avtakende grensenytte når det gjelder konsum, som ganske enkelt betyr at selv om vi opplever økt nytte (glede/tilfredshet) ved økt konsum, så avtar nytten jo mer vi konsumerer. Det betyr at du har mer glede av den første millionen du tjener enn av den tiende millionen. Du har mer nytte av den første ferieuken enn av den fjerde osv. Vi mennesker har også en naturlig tendens til å oppleve høyere nytte av et konsum i dag fremfor å utsette det til i morgen.

På samme måte som en bedrift har en balanse bestående av eiendeler på den ene siden, og egenkapital og gjeld på den andre, har også husholdningene eiendeler og forpliktelser.

Husholdningenes eiendeler og forpliktelser (fra Personlig Finans av Trond Døskeland)

Den som kjenner balansen til en bedrift vil se at husholdningenes balanse inneholder noen andre elementer, som f.eks. boligkonsum og humankapital. Boligkonsum er enkelt forklart summen av det vi kommer til å måtte betale for å bo gjennom livet. Humankapital er ganske enkelt dagens verdi av vår fremtidige inntekt (hvis vi hadde fått utbetalt all fremtidig inntekt i dag). Som vi ser av figuren har vi en del egenkapital, men for oss unge er det meste av dette ikke frigjorte midler. De er knyttet til vår fremtidige inntekt. Etterhvert som vi blir eldre vil vi få utbetalt mer av vår humankapital, som derfor blir til finansiell kapital, og mer av vår gjeld blir forhåpentligvis omgjort til egenkapital.

For oss mennesker føles det mest komfortabelt å fordele konsumet vårt over vår levetid – et konsept som kalles konsumglatting. Grunnen til det kan vi jo si å være at alternativet er ganske mye tristere. Da kunne vi konsumert kun i den tiden vi var yrkesaktive og tjente penger, og hadde ikke hatt noe annet valg enn å dø etter vi sluttet å jobbe. Konsumglatting betyr ikke nødvendigvis at vi vil konsumere like mye i alderen 20-30 som i alderen 40-50, selv om figuren under tilsier det, men at veksten eller reduksjonen i konsum bør være relativt jevn, slik at vi ikke får brå endringer. Det er derfor vi sparer, og derfor vi låner. Når vi sparer til pensjon, er det fordi vi ønsker å ha et konsum også etter vi slutter å ha en arbeidsinntekt.

Vi modererer derfor konsumet vårt i den tiden vi er yrkesaktive, og flytter dette til pensjonisttiden vår. Vi flytter konsum fra i dag til fremtiden. Lån er akkurat det samme – bare motsatt. Man flytter konsum (eller investering) fra fremtiden, til i dag. Samtidig flytter man kapital fra fremtiden til i dag. Lån er i så måte konsum (eller investering) som vi enda ikke har betalt for. Vi låner penger i dag, og banken sier at det er greit, fordi du betaler renter og fordi din fremtidige inntekt (din humankapital) gjør deg i stand til å betale tilbake lånet. I tillegg sikrer de seg kanskje ved at de tar sikkerhet i selve gjenstanden du lånefinansierer.

I tillegg er det andre årsaker, eksempelvis skattemessige, til å ta opp lån, men det tar jeg ikke opp i dette innlegget.

Livssylushypotesen (Modigliani), bilde hentet fra Hellebostad og Mauring

Når vi ser på sparing, så ser vi at man når en topp når man kommer til pensjonsalder. Når det gjelder lån, er det stort sett unge mennesker troner. Dette er i trå med hypotsen om konsumglatting. Dette er typisk blanding av lån til forbruk og lån til investering. Det er imidlertid boliglån som er den store tyngden. Vi kan se at vi i snitt låner mest i det vi runder 40. Vi ser også at det fortatt er noe gjeld igjen helt frem til vi dør. Er det rimelig? Man kan i hvertfall tenke seg at det å nedbetale lån er en form for sparing, og ut fra det jeg skrev tidligere om konsumglatting, så vet vi at vi sparer helt frem til vi når pensjonsalder. Dette ser ut til å vise at vi har økt behov for bolig frem til vi er rundt 40. Det er kanskje typisk rundt den alderen man har fått den familiestørrelsen man forventer å ha, så at gjelden øker gradvis opp mot 40 reflekterer nok forventning til boligkonsumet vårt.

Banken

Vi har nå sett at fordeling av konsum over levetiden er viktig for oss mennesker, og at sparing og lån er to viktige verktøy for å oppnå dette. Det er derfor lett å se at banken spiller en viktig rolle i samfunnet.

En bank har mange oppgaver, og bank i dag er ikke det samme som bank i går, og det er i hvertfall ikke det samme som bank i morgen. For alle praktiske formål skal vi se på den “tradisjonelle banken”, og forholde oss til det vi i dag fremdeles anser som dens kjerneoppgaver. Den mest sentrale rollen til banken er å være et bindeledd for de som har penger og de som trenger penger.

Kort oppsummert lever banken av at de henter penger inn, og låner dem ut igjen. Banken får inn penger gjennom kundeinnskudd eller finansiering i markedene (markedsfinansiering). Eksempel på markedsfinansiering kan være obligasjonslån. En obligasjon er ganske enkelt forklart et verdipapir man kjøper til en pris X (“pålydende“), som gir eieren rett på en rente av X som vanligvis utbetales i terminer (f.eks årlig). Ved forfall tilbakebetales pålydende (X kroner). Her er det mye variasjon, og noen banker baserer seg kun på innskudd. Årsaken til det kan være flere, men for rene forbrukslånsbanker skyldes det som regel at de sliter med å få markedsfinansiering. Grunnen til det er at kundeinnskudd er dekket av en garantiordning, som gjør at hvis banken går konkurs får du tilbake innskuddet du hadde i den banken fra denne garantiordningen (opp til to millioner kroner per bank). Innskudd opp til 2 millioner er derfor risikofri for den som setter de inn. Markedsfinansiering (som f.eks. obligasjonslån) betyr imidlertid en risiko for den som låner ut penger til banken (risiko for ikke å få tilbake pengene dersom banken går konkurs). Forbrukslånsbanker tar veldig høy risiko på sine utlån, og risikoen gjør at de sliter med å få billig finansiering fra annet enn kundeinnskudd.

Uansett hvordan banken finansierer utlånene er målet å skaffe en billig og stabil finansiering, og å låne ut disse med høye renter, til låntakere som representerer lav risiko. I tillegg er det naturligvis viktig for banken å ha gode systemer og rutiner som gjør at man drifter virksomheten billig og effektivt.

Hvordan setter banken sine utlånsrenter?

Er det noe folk er opptatt av, er det bompenger og rentene på lån. Dette fordi det ofte er store utgiftsposter i vår hverdag.

Lån er et produkt som hvilket som helst annet, og banken er opptatt av å dekke inn produktets kostnad, og samtidig sitte igjen med en fortjeneste. Fortjenesten er viktig. Vi har allerede stadfestet at banken spiller en viktig rolle i samfunnet, og for at en bank skal kunne utspille denne rollen må den være lønnsom. Bankens margin vil naturligvis avhenge av flere ting, som f.eks. prisstrategi og konkurransesituasjonen. Vanligvis setter banken rentene så høyt de kan ut fra omstendighetene, men det er ingen hemmelighet at det går an å prute på renten, og offensive kunder som orker å ta den årlige prutesamtalen med banken kan godt tenkes å ha lavere rente enn de som bare “lar det skure”. Gode kunder har ofte bedre rente enn risikoen kanskje skulle tilsi. Det betyr ikke nødvendigvis at du som “normal” kunde betaler en høyere rente for å subsidiere gode kunder, men at banken henter inn den reduserte marginen på disse kundenes langsiktige og som regel omfattende kundeforhold.

En kalkyle for en lånerente vil derfor ikke være ulik en kalkyle for et annet produkt. Kalkylen ser slik ut:

Fundingkostnad
+ Driftskostnad
+ Risikokostnad
+ Fortjeneste_______________
= Salgspris (utlånsrente)

Vi splitter altså lånets kostnad inn i tre. Jeg tar kort for meg alle tre, for den som er interessert.

Fundingkostnad:
Kan oversettes til “innlånskostnad”, og kan sammenlignes med en innkjøpspris. Dette er kostnaden banken har på pengene de låner ut.

Mange tror at banken låner pengene sine fra Norges Bank, og at styringsrenten derfor er den renten banken låner pengene sine til. Dette er feil. Styringsrenten er en innskuddsrente som bankene kan få ved å sette pengene sine i Norges Bank (innenfor en gitt kvote). Man kan si at styringsrenten er bankenes alternativkostnad ved å låne ut penger. Slik kan vi se at styringsrenten danner et gulv for hva bankene er villige til å låne ut penger for, fordi de låner i hvertfall ikke ut penger til mindre enn det de kan få ved å sette pengene i Norges Bank. I tillegg til å være en innskuddsrente har styringsrenten den funksjon at den signaliserer en forventning til fremtidig inflasjon og økonomisk utvikling, noe som er grunnen til at den ofte kalles “signalrenten”.

Så, hvis bankene ikke låner pengene sine av Norges Bank, hvor får de tak i dem da?

Banken har tre hovedkilder til funding:
– Kundeinnskudd (de pengene vi som kunder setter inn i banken)
– Markedsfinansiering (typisk innskudd fra andre banker og obligasjonslån/verdipapirgjeld).
– Egenkapital

En relativt større andel av bankens totale finansiering består i dag av markedsfinansiering enn for noen år siden. Eksempelvis finansieres flere boliglån med såkalte OMF (obligasjoner med fortrinnsrett) samt vanlige bankobligasjonslån. Likevel tenker man gjerne på fundingkostnaden som en interbankrente (rente i bankmarkedet), uten at jeg i dette innlegget skal gå nærmere inn på hvorfor det er slik. En stor del av bankenes finansiering prises derfor med utgangspunkt i tremåneders NIBOR (pengemarkedsrenten med tre måneders løpetid). NIBOR gjenspeiler den renten en bank må betale for et usikret lån av en annen bank. NIBOR trenger ikke være så lett å forstå, men for å forklare det enkelt bestemmes den av markedets forvetning til gjennomsnittlig styringsrente de neste tre månedene + et risikopåslag. Dette risikopåslaget kan variere, og stiger typisk i tider med uro og usikkerhet i markedene, noe som fører til at bankenes fundingkostnader kan stige uten at styringsrenten endres.

I tillegg til pengemarkedsrenten må bankene betale et ekstra risikopåslag. Dette risikopåslaget er blant annet avhengig av bankens kredittverdighet. Jo mer kredittverdig en bank er, jo lavere blir typisk påslaget. En bank med høy kredittverdighet og lave risikopåslag kan derfor ha konkurransefortrinn over andre banker som må betale mer for sin funding.

Bankenes funding er naturligvis et stort tema, så jeg skal stoppe her. Det viktigste jeg vil at du skal ta med deg fra dette delkapitlet er at det ikke er noe 1:1-forhold mellom styringsrente og fundingkostnad. Det vil si at det ikke er en selvfølge at dersom styringsrenten går ned/opp med 0,25 prosentpoeng, så skal man få en tilsvarende reduksjon/økning i boliglånsrenta.

Driftskostnad:
Typisk kostnader knyttet til personal, banksystemer osv. Dette må jo også dekkes inn.

Risikokostnad:
Et hvert lån betyr risiko for banken. Hovedsaklig tenker vi på risiko for at de ikke får pengene tilbake – ikke alle lån blir tilbakebetalt. Derfor må banken legge på en margin som skal dekke de forventede tapene. I tillegg krever myndighetene at banken også må sette til side penger for tap utover det de forventer, slik at de ikke går konkurs dersom de taper litt penger. Jo mer myndighetene sier at banken må sette til side for å være forsiktig, jo høyere blir renten. Jeg skal forklare hvorfor. Investorene krever avkastning av kapitalen – og det gjelder også for den kapitalen som ikke kan lånes ut på grunn av myndighetenes krav. For å sørge for avkastning på pengene man ikke har lånt ut, må man ha bedre avkastning på pengene man låner ut, og da blir prispåslaget på utlånte penger høyere. Dette var blant annet grunnen til at rentene gikk opp da myndighetene satte økte kapitalkrav, som var utgangspunktet for Rune Bjerkes famøse “spleiselag” i 2013.

Risikokostnaden for bankene (som er relevant for utlån) deles hovedsaklig inn i fire, som jeg skal forklare kort (for de som er spesielt interessert):

Kredittrisiko: risikoen for at hele eller deler av lånet ikke blir tilbakebetalt som følge av at bankens motpart (kunder) ikke oppfyller sine forpliktelser. Selv om gjeldsbelastingen blant norske husstander i de siste årene har økt, er misligholdsraten lav. Banker er generelt sårbare for tap, ettersom bankens eiendeler stort sett består av utlånte penger, som primært er finansiert med innskudd fra kunder eller markedsfinansiering. Egenkapitalen utgjør en svært liten del, og står i fare for å forsvinne dersom banken får store tap. Derfor er også myndighetene ekstra påpasselige med at bankene i hvertfall holder et minimumsnivå av egenkapital.

Likviditetsrisiko: risiko knyttet til at banken ikke klarer å innfri sine forpliktelser og risiko for inntjening som følge av likviditeten i markedet og potensiell mangel på funding (redusert tilgang på funding vil jo føre til at banken må redusere sitt aktivitetsnivå.). Likviditetsrisikoen vil med andre ord avhenge av hvordan banken finansierer seg, men hvis banken låner ut 4 millioner i et boliglån med 25 års løpetid, er det kanskje dumt om banken har finansiert dette med et lån de må tilbakebetale om et halvt år. Da kan de få problemer med likviditeten. Det var det vi så i Norge i 2008, at bankene sine lån forfalt, og de utlånene som banken har forfaller mye senere. Selv om de hadde verdier i form av utlån, hadde de ikke har cash til å betale sine egne lån. Dette kan føre til, og har ført til, at staten må gå inn og dekke den ekstra likviditeten for å unngå store samfunnsmessige tap ved at banken går konkurs.

Markedsrisiko: risiko som oppstår som følge av at banken har åpne posisjoner i f.eks valuta-, rente- og kapitalmarkeder. Markedsrisiko innbefatter også risiko knyttet til variasjon i resultat som følge av endringer i markedspriser. De fleste banker skiller mellom ulike former for markedsrisiko, men dette er ikke hensiktsmessig å gå nærmere inn på.

Driftsrisiko: Kan f.eks være. risiko for eksterne hendelser som påvirker bankens interesser (konkurranse, politikk osv). Det kan også være operasjonell risiko knyttet til menneskelig svikt, prosessvikt, ansatte som svindler banken og tap av omdømme.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Nominell og effektiv rente

Når man skal sammenligne lån er det viktig at man sammenligner totale kostander. Nominell rente er lett å forstå for de fleste, og kan forklares som den rene renten som beregnes ut fra restsaldo på lånet. Nominell rente utgjør som regel en stor andel av den totale kostnaden for lånet, men det er ofte flere kostnader forbundet med lån (eksempelvis etablerings- og termingebyrer). Som vi skal se senere i innlegget, kan disse kostnadene utgjøre mer en selve renten. Den totale kostnaden for lånet er representert i den effektive renten. Den effektive renten avhenger primært av:

Den nominelle renten på lånet
Lånebeløpet
Nedbetalingstid
Eventuelle gebyrer og deres størrelse
Det er noen flere variabler som kan påvirke effektiv rente, som f.eks avdragsprofil, men av praktiske formål forholder vi oss til de overnevnte i dette innlegget. Jeg kommer tilbake til avdragsprofil mot slutten av innlegget.

Den nominelle renten er den årlige renten som beregnes av restgjelden på lånet og har åpenbart innvirkning på totalkostnaden.
Lånebeløpet har innvirkning på effektiv rente dersom lånet har gebyrer. Jo lavere lånebeløp (alt annet likt), jo høyere effektiv rente. Årsaken til det er at gebyrene er de samme, uavhengig av lånebeløpet, så jo lavere lånebeløp jo større blir gebyrene relativt til lånebeløpet. Eksempelvis er 2.000 kroner et relativt høyt gebyr for et lån på 20.000 kroner (10%), mens for et lån på 2.000.000 vil gebyret være en lavere prosent av lånebeløpet.
Nedbetalingstiden har innvirkning på effektiv rente dersom lånet har etableringsgebyrer. Jo lavere nedbetalingstid, jo færre år å “spre” gebyrene over, og jo høyere blir årlig effektiv rente. Det betyr selvfølgelig ikke at det er billigere å øke nedbetalingstiden.
Gebyrenes størrelse har åpenbart innvirkning på effektiv rente. Jo høyere gebyrer, jo høyere effektiv rente.

Når du skal sammenligne lånetilbud er det åpenbart viktig å sammenligne effektiv rente, da det er denne som best reflekterer hva totalkostnaden vil være. Ettersom effektiv rente avhenger av de overstående faktorene er det også viktig at du sammenligner tilbud på to identiske lån. Du kan for eksempel ikke sammenligne effektiv rente på et lånetilbud på 100.000 over 4 år med effektiv rente på et lånetilbud på 500.000 over 8 år. Da sammenligner du epler og pærer, og vil ha et dårlig beslutningsgrunnlag.

Mangel på kunnskap omkring forskjellen på nominell og effektiv rente er etter min erfaring ganske vanlig blant folk. Heldigvis er avvikene mellom nominell og effektiv rente ofte forsvinnende små på et gjennomsnittlig boliglån, som gjør at sammenligning av nominell fremfor effektiv rente på slike lån ikke har særlig stor betydning. Etableringsomkostningene er et engangsbeløp som betales ved lånets opptak, og termingebyrene (som vanligvis ligger mellom 0-70 kroner) utgjør også en relativt liten andel av lånets totalkostnad.

Åpenbart vil avviket mellom nominell og effektiv rente være større på billån og forbrukslån enn på et boliglån, ettersom det normalt sett er snakk om vesentlig lavere lån. Her er det dessverre noen låntilbydere som gjør store penger på å utnytte kunnskapsløsheten blant folk, og jeg kommer tilbake til dette når jeg skal skrive om billån.

Det er ikke bare banken som bestemmer

Norske banker er underlagt mange lover og retningslinjer. I tillegg til lover som f.eks. Finansforetaksloven, Finansavtaleloven og Hvitvaskingsloven er banken også underlagt strenge retningslinjer fra ulike tilsyn. Mest sentralt er Finanstilsynet. Finanstilsynet er underlagt Finansdepartementet og har til hensikt å føre tilsyn med finans- og forsikringsinstitusjoner for å bidra til stabilitet i markedet gjennom å sikre god soliditet, risikobevissthet, styring og kontroll i foretakene. Finanstilsynet har laget forskrifter som har en direkte innvirkning på hvordan banken må vurdere sine kunder.

Det er flere gode grunner til at man bør følge nøye med på hva bankene gjør, og legge føringer for deres virksomhet. Til syvende og sist, dersom bankene tar for høy risiko og ikke er solide nok til å ta tap, er det staten som må dekke de enorme kostandene som påføres samfunnet som følge av at en bank går konkurs. Mange aktører, spesielt forbrukslånsbanker, utnytter dessuten folks mangel på økonomisk kunnskap, og kan bokstavelig talt ødelegge livene deres. Det er derfor viktig å ha lover og regler som beskytter forbrukerne mot useriøse aktører og praksiser som kan skade både enkeltindivider og samfunn.

Dersom bankene ikke følger retningslinjene og påleggene fra Finanstilsynet kan de miste rettigheten til å drive bank. Du kan kanskje tenke at banken er veldig firkantete noen ganger – og årsaken til det er som regel at det ville føre til brudd på lover eller gjeldende retningslinjer dersom de skulle etterkomme ditt ønske. Ingen kunde er god nok, ingen enkeltperson så viktig, og ingen situasjon så spesiell at banken er villig til å ofre sitt eksistensgrunnlag for å tilfredsstille deg.

Jeg skal komme tilbake til konkrete retningslinjer når vi går nærmere inn på hvordan bankene vurderer deg for lån.

Hvordan vurderes man for lån?

Før i tiden var det vanlig å få lån basert på “sitt ærlige ansikt”. Sånn er det ikke lengre, og mange banker føler ikke en gang behov for å se ditt “ærlige ansikt” før de gir deg lån. Digitale løsninger gjør at banken kan ta en grundig objektiv vurdering av din kredittverdighet. Det betyr ikke at troverdighet og relasjoner ikke har noe å si lengre. For banken handler det først og fremst om hvorvidt de kan forvente at du betaler tilbake det du skylder inkludert renter.

Kredittvurdering har på flere måter gått fra å være et rent bankhåndtverk til å bli relativt gjennomregulert av myndighetene. Det vi skal se i de kommende avsnittene er at det er flere gode grunner til at bankene bør holdes litt etter ørene. Vi skal også se at det fremdeles er aspekter ved kredittvurderingen som foregår ulikt fra bank til bank, blant annet på grunn av at de har ulike rutiner, strategier og interne retningslinjer.

Det ligger i sakens natur at man før en slik vurdering først vil ha avdekket hva det faktiske lånebehovet er. Det kan være vesentlige avvik mellom lånebehov og hva man faktisk kan få i lån, slik at man vil måtte tåle en realitetsorientering – men lånebehovet vil som regel alltid være utgangspunktet.

Jeg vil også understreke at prosessen for vurdering av lån, selv om de baserer seg på samme prinsipp, kan være ulik fra lån til lån. Eksempelvis vil det være større behov for å vurdere langsiktighet i den økonomiske situasjonen når man vurderer et boliglån enn et billån eller kortsiktig forbrukslån. Det betyr ikke at banken kan tillate seg å være slepphendt i vurderingen av noen av lånene, men illustrerer at kredittvurderingen må tilpasses det underforliggende formål.

Betjeningsvilje og betjeningsevne

Betjeningsvilje handler om hvor flink du er til å betale tilbake det du skylder. Dette er ikke knyttet opp til din inntekt eller formue, men til om du faktisk betaler det du skylder. Betjeningsevne er derimot knyttet opp mot din faktiske økonomiske evne til å betale dine forpliktelser i tide. Dersom du har penger på konto, men bare ikke orker/husker å betale regningene dine i tide, sier vi at du har dårlig betjeningsvilje. Dersom du ikke klarer å “få endene til å møtes” sier vi at du har dårlig betjeningsevne. Du kan også høre begreper som “dårlig likviditet” og “insolvens”. Det betyr det samme; du er ikke i stand til å innfri dine forpliktelser innen de forfaller.

“En purring er vel ikke så farlig, så lenge jeg betaler til slutt?”
Dette er en ganske vanlig feiloppfatning, men selv en andregangspurring kan føre til at du ikke får lån når du ønsker det. Selv om en andregangspurring ikke er like alvorlig som inkasso, er det likevel ofte et tegn på din betjeningsvilje – og de fleste banker vil ta din purrehistorikk i hvertfall de siste 6-24 månedene med i vurderingen når de vurderer deg for lån. Det vil kunne påvirke hvilken risikoklasse du havner i. Risikoklasse er et begrep jeg ikke skal gå nærme innpå i dette innlegget. Hvis du har relativt ferske purringer (6-24 mnd), kan du få beskjed om at banken ikke ønsker å gi deg et lån før du har vist plettfri betalingshisotrikk i noen måneder fremover.

I tillegg til historikk banken har på deg i sine egne systemer innhenter banken også kredittvurderinger fra kredittvurderingsselskaper som f.eks Bisnode. Her vil banken få tilgang til informasjon fra eksterne kilder om blant annet betalingsanmerkninger. Dersom et selskap har et krav mot deg, vil du kunne stå oppført med betalingsanmerkning her. Banken kan ikke nødvendigvis se hva det gjelder, men så lenge du har betalingsanmerkning blir sannsynligvis ikke søknaden din vurdert. De fleste seriøse banker har en policy om ikke å gi lån til personer med betalingsanmerkning. Dette er ikke noe som er omfattet av lovbestemmelser direkte, men er en del av de aller fleste bankers interne kredittpolicy.

Interne anmerkninger vil banken kunne lagre så lenge du lever. Det betyr, for å sette det litt på spissen, at dersom du ikke betaler kredittkortregninga di, og banken taper penger som følge av dette, kan det forhindre deg i å få lån i den banken – potensielt resten av livet.

Dersom du vil ha noe som helst å gjøre med en bank fremover: ikke påfør dem tap…

Inntekt, utgift og likviditetsoverskudd

Bankene behandler (dessverre?) inntekt litt ulikt. Hovedregelen er at kun fast og varig inntekt skal vurderes. Med fast inntekt menes den inntekt du har kontraktsfestet i form av en fast stilling i en arbeidskontrakt, dine faste pensjonsutbetalinger eller et vedtak (eksempelvis vedtak om uføretrygd). Variable tillegg, provisjoner og bonuser blir i utgangspunktet ikke tatt med i betraktningen. Det betyr ikke at en selger som jobber på provisjon aldri kan få lån. Kan du vise til stabile tall over tid kan det være godt nok. Det gjelder også f.eks. arbeidsavklaringspenger, som er en midlertidig stønad, med mindre det kan dokumenteres at disse vil gå over i en eller annen form for fast stønad. Igjen, det handler om hvorvidt inntekten kan vurderes til å være fast og varig, og det er i stor grad opp til banken å vurdere hva de anser som stabilt. Eksempelvis kan enkelte yrker og utdanningsnivåer være grunnlag for å anta mer stabilitet enn andre.

Leieinntekt kan ofte medregnes dersom denne er stabil og kan dokumenteres. Ikke alle banker regner med 100% av leieinntektene per år. Noen regner med bare en gitt prosent, eller f.eks bare 10 måneders leie. Dette skal blant annet ta hensyn til kostnadene knyttet til utleie, samt muligheten for at man kan være uten leieinntekt noen måneder. Dersom leieinntektene er skattepliktige vil inntektene justeres for skatt.

Når den faste inntekten er avklart, skal banken også ta hensyn til dine utgifter. Referansebudsjettet fra SIFO benyttes gjerne til å beregne et forventet månedlig konsum basert på situasjonen i ditt hushold, som kan anses som et minimumskonsum (noen ganger kalt livsoppholdssats). Referansebudsjettet omfatter normale utgifter for et hushold, men tar ikke hensyn til f.eks. boutgifter, ferier og kvelder på byen. Dette er altså noe banken må hensynta i tillegg. I forbindelse med søknad om boliglån vil jo som regel boutgiftene primært være renter og avdrag på lån, i tillegg til forsikringskostnader, strøm, vedlikehold etc. Det er sjelden banken spør deg hvor ofte du drar på byen, og en grunn til det er jo at dette er utgifter du lett kan unngå dersom du ser at budsjettet ditt ikke tillater det. Budsjettet banken tar utgangspunkt i kan derfor gjøre at du kommer opp med høyere (men også noen ganger lavere) overskudd hver måned enn hva som er realiteten. Søker du billån og bor hjemme hos foreldrene dine kan det argumenteres for at du har lave boutgifter, og at dine reelle månedlige utgifter ligger tett inntil livsoppholdssatsen. Naturligvis blir kostnader forbundet med å eie bil regnet med.

På slutten av måneden skal du sitte igjen med minimum 0 kroner i det vi kaller “likviditetsoverskudd”. Dette beregnes slik:

Bruttoinntekt
– Skatt
= Nettoinntekt
– Konsum
– Rente
– Avdrag
= Likvditetsoverskudd

Dessuten skal banken ta høyde for at du skal ha et positivt likviditetsoverskudd også etter en renteøkning på så mye som 5 prosentpoeng. For å illustrere hvor mye det utgjør, så kan vi ta utgangspunkt i et lån på 2.000.000 over 25 år. Med dagens rentenivå, med f.eks 2,5% rente vil lånet koste 9.022 per måned i renter og avdrag. Øker vi det til 7,5% rente er terminbeløpet 14.830 pr mnd – en økning på nesten 6.000 kroner per måned (en 64% økning i månedlig utgift!)

Terminbeløpet du betaler på lånet ditt er splittet inn i renter og avdrag (og eventuelt termingebyr). Avdrag er selve nedbetalingen du gjør på lånet, som reduserer restgjelden. Rentene er kostnaden. F.eks. på et lån på 1000 kroner, dersom du betaler 100 kroner, hvorav 40 er avdrag og 60 er renter, er restgjelden etter innbetalingen 1000 – 40 = 960 kroner. Mange vil kanskje si at avdrag ikke er en kostnad, men heller en “innbetaling til seg selv”, og at det derfor ikke burde være med i budsjettet. Selv om det ikke er en kostnad er det en utgift som må betales og som påvirker hva du sitter igjen med i måneden.

Du kan oppleve at bankene er veldig nøye på å få oversendt dokumentasjon på inntekten din, selv om du kanskje føler det er unødvendig mye. Dette er fordi de kan bli pålagt å fremlegge dokumentasjon på at banken har gjort en grundig og forsvarlig kredittvurdering av deg, hvis myndighetene kommer på kontroll.

Dersom din inntekt i dag er god nok, men at den fremover kan være usikker (eks. hvis bedriften du jobber i har kommunisert ut at de kommer til å foreta nedbemanning), kan dette resultere i avslag. Det er bankens ansvar å ta hensyn til slike forhold. Det finnes også en rekke forhold – økonomiske og ikke-økonomiske, som gir banken et etisk ansvar til ikke å innvilge lån.

Egenkapital

Selv om ikke alle lån krever egenkapital, vil det likevel kunne være en avgjørende faktor. Et eksempel kan være en ung kunde, med “på grensa” inntekt som søker lån til bil. Da vil det kunne spille positivt inn om kunden stiller med egenkapital. Det gir banken en ekstra sikkerhet ved at forholdet mellom lånebeløp og bilens verdi blir bedret. Dessuten kan det være et tegn på at du har evne til å sette av penger til sparing. Hvis du stiller med egenkapital vil du dessuten kunne forvente en bedre rente enn ved fullfinansiering, ettersom risikoen for banken blir lavere. Når det gjelder boliglån vil du, etterhvert som du har begynt å nedbetale lånet ditt (og boligen kanskje har steget i verdi) kunne forhandle frem en bedre rente, ettersom belåningsgraden er blitt lavere og risikoen for banken derfor er lavere. Det samme kan vi ikke si på billån, ettersom bilen med all sannsynlighet har sunket i verdi samtidig som du har nedbetalt lånet.

Gjeld

Hvor mye gjeld du har fra før er avgjørende for hvor mye gjeld du kan ta opp. Én vurdering banken kan gjøre, er å se på om summen av alle dine gjeldsforpliktelser hver måned allerede er så høy at du risikerer å få likviditetsunderskudd ved nytt lånopptak. I tillegg sier Finanstilsynets retningslinjer at maksimal gjeldsbelastning du kan ha er 5 ganger bruttoinntekten din (altså før skatt). Dette gjelder både boliglån, billån (i praksis de fleste gjenstandslån) og forbrukslån. Ditt studielån vil også telle med i denne totalen. Det betyr at for en person som tjener 15.000 i måneden før skatt, vil maksimal gjeld som kan innvilges være: 15.000*12*5=900.000 kroner.
Har personen allerede 900.000 kroner i gjeld, kan ikke banken innvilge mer gjeld, uten å bryte retningslinjene fra Finanstilsynet. Har personen allerede 800.000 kroner i gjeld, kan banken innvilge maksimalt 100.000 i ny gjeld.

Kundeforholdet ditt

Det er vanlig å ha noen bankprodukter her, og andre produkter der. Kanskje er du LO-medlem slik at du ønsker å ha forsikringene dine hos Sparebank 1, mens du har brukskonto og kredittkort hos Danske Bank fordi det var der foreldrene dine opprettet brukskontoen din da du var liten, mens billånet står i DNB fordi der fikk du best rente? Ofte er det når man skal gjøre investeringer som hus og bil at man begynner å lete rundt etter andre alternativer enn banken man har “vokst opp med”. En helt ny kunde betyr liten kjennskap til kunden utover det man får fra ekstern kredittscore og innhenting av lønnsdokumentasjon. Det er utvilsomt positivt at banken har kjennskap til deg, selv om det nok betyr mindre i dag enn for noen år siden, ettersom digitale løsninger gjør det lettere å “bli kjent med deg”. Det er nok oftest i tvilstilfellene at kundeforholdet ditt (gitt at det stort sett er et bra kundeforhold) kan være det som avgjør utfallet av din søknad. Når det gjelder boliglån er det noen banker som krever at du har lønnsinngang i deres bank for at de skal innvilge lån.

I dag er det veldig lett å opprette kundeforhold i en ny bank. Alt du trenger er som regel bankID fra din primærbank, så er du good to go.

Sikkerhet

Banken er også opptatt av sikkerheten for lånet. Skal du ha et lån til en noenlunde grei rente, må du stille med sikkerhet. Tar du boliglån, tar banken sikkerhet i boligen (pant). Tar du billån, tar banken sikkerhet i bilen (salgspant). Tar du et usikret lån (forbrukslån) har ikke banken noen sikkerhet utover ditt løfte om at du skal betale tilbake. Denne økte risikoen gjenspeiles i en høy rente. Som vi skal se i det neste avsnittet, er det ikke alt banken på en praktisk måte kan ta sikkerhet i.

Pant og salgspant

Når man kjøper en bolig med lånefinansiering etablerer banken normalt pant i boligen. Dette gir banken mulighet til å kreve at boligen selges for å innfri lånet dersom du ikke betaler dette i henhold til nedbetalingsplanen. For at pantet skal få rettsvern, tinglyses det i et register som kalles grunnboken. Dette er et offentlig register over tinglyste heftelser og rettigheter i fast eiendom (og andeler av borettslag). Tinglysning innebærer at den retten banken har til å kreve boligen solgt for å innfri sine krav, blir tinglyst til det offentlige. Et pant kan som hovedregel når som helst etableres i en eiendom du allerede eier. Det eneste kravet som stilles er at panteobjektet er et (eller flere) formuesgoder. I dette ligger det at det må ha økonomisk verdi, altså at det kan gjøres om til penger gjennom salg eller utleie.

Et salgspant derimot kan kun etableres i forbindelse med et reelt salg, og det kan kun etableres salgspant i løsøre (altså fysiske ting som ikke er fast eiendom. Eiendom kan ikke beheftes med salgspant). At salgspant må inngås “i forbindelse med salg”, betyr altså at avtalen om salgspant må knyttes til et reelt salg. Det vil si et salg som bringer nye verdier inn i kjøperens formue. Det vil si at man ikke kan stifte salgspant i en eiendel man allerede eier. En person kan heller ikke selge en bil til en annen person, og så kjøpe den tilbake på kreditt mot salgspant. I et slikt tilfelle vil det ikke være et reelt salg, og salgspantet vil ikke være gyldig.

Det er verdt å merke seg at det jeg skriver om i dette innlegget er det vi kaller avtalepant, altså hvor pantet er et resultat av en avtale mellom pantsetteren (vanligvis låntaker) og panthaver (vanligvis banken). Det kan også ta utleggspant i eiendeler. Dette skjer i de tilfeller hvor kreditor ikke har rettsgyldig pant til å dekke utestående krav, for eksempel ved mislighold av forbrukslån. Kreditor må i disse tilfellene begjære utlegg gjennom namsmannen. Mer om det i et annet innlegg.

Boliglån

Boliglån er lån med sikkerhet i bolig. Når man låner med sikkerhet i bolig tar banken pant i boligen.

Når man skal kjøpe en bolig setter man gjerne i gang med å søke om et finansieringsbevis. Dette gjør man både for å kunne dokumentere overfor selger at man faktisk kan finansiere kjøpet, og for å selv få et realistisk bilde av hva man kan kjøpe bolig for. I denne prosessen er det mange som får en realitetsorientering, hvis de selv har bedømmet sin låneevne til å være mye høyere enn det banken gjør. Du kan søke om finansieringsbevis fra flere banker, og det er stort sett bindende for banken. Imidlertid er det flere forhold som gjør det mulig for banken å trekke finansieringsbeviset tilbake, f.eks. dersom du har oppgitt ukorrekt informasjon, eller inntekts- eller gjeldssituasjonen endrer seg. Finansieringsbevis er normalt gyldige i tre måneder. Dersom du legger inn bud, vil megler sjekke om finansieringen er i orden. Det vanlige er at megler ringer banken. Det er ikke å anbefale å vise finansieringsbeviset til megler før etter budet er akseptert, ettersom megleren da vet hva du maksimalt kan betale, og nok vil forsøke pushe prisen opp.

Du kan oppleve å få finansieringsbevis på ulike beløp hos ulike banker. Dette er fordi hver bank har sin egen vurderingsprosess, kriterier og risikostrategi. To ulike banker kan f.eks. vurdere din betalingsevne ulikt. Det kan også tenkes at en bank har intern historikk som andre banker ikke har tilgang til. Dessuten er det dessverre noen banker som ikke er like nøye med å følge Finanstilsynets retningslinjer. Det er ikke nødvendigvis den banken som tilbyr deg mest lån, som er den beste banken for deg. Du må derfor gjøre dine egne vurderinger av din egen betalingsevne både på kort og lang sikt. En god bank vil være nøye med å informere deg om konsekvensen for økonomien din ved f.eks en renteøkning (og faktisk er de lovpålagt å gjøre det).

Valg av bolig kan ha betydning, ettersom boligen er sikkerheten for lånet – men det er sjelden at banken setter seg på bakbeina. Det kan imidlertid skje at banken vurderer boligens verdi til å være vesentlig lavere enn kjøpesummen. Med dagens relativt høye boligpriser har flere banken blitt mer kritisk til om kjøpesummen egentlig er en forsvarlig indikasjon på den faktiske verdien. I finansieringsbeviset står det gjerne en maksimal kjøpesum, gitt en fri egenkapital. Det er viktig å huske at ved kjøp av borettslagsleilighet med andel av fellesgjeld, vil denne bli fratrukket den maksimale lånesummen i finansieringsbeviset. Med andre ord vil maksimal kjøpesum i finansieringsbeviset være inkludert eventuell andel av fellesgjeld.

Renten du får på boliglånet ditt avhenger av flere ting. Jeg skrev litt om bankenes prising av lån tidligere. Bolig er generelt sett objekter med god sikkerhet, ved at risikoen for at den taper seg veldig i verdi over tid er lav. Risikopåslaget er derfor ganske lavt, og renten på boliglån er derfor generelt sett lave. Du skal kunne forvente at renten er lavere dersom du har belånt 50% av boligens verdi enn om du har belånt 85% av boligens verdi. Jo lavere belåningsgrad, jo bedre sikkerhet har banken for lånet, og jo bedre rente skal du kunne forvente.

Boliglånsforskriften

(Forskrift om krav til nye utlån med pant i bolig). Dette er en forskrift som er kommet først og fremst på grunn av den økende gjeldsbelastningen blant norske husholdninger. Den setter en rekke begrensninger på nye utlån med pant i bolig. Kort oppsummert sier den dette:

For Oslo	For resten av landet
Lånekundens samlede gjeld skal ikke overstige fem ganger bruttoinntekt (inkl forbrukslån, studielån osv.)	Lånekundens samlede gjeld skal ikke overstige fem ganger bruttoinntekt (inkl forbrukslån, studielån osv.)
Det skal kreves minst 40% egenkapital ved kjøp av sekundærbolig (bolig nr 2, 3 osv)
Det skal kreves 15% egenkapital ved kjøp av primærbolig.	Det skal kreves 15% egenkapital ved kjøp av primærbolig.
Avdrag kreves for lån som overstiger 60% av boligens verdi.	Avdrag kreves for lån som overstiger 60% av boligens verdi.
Rammelån kan ikke gis når lånerammen overstiger 60% av boligens verdi.	Rammelån kan ikke gis når lånerammen overstiger 60% av boligens verdi.

Banken kan gjøre unntak utenfor kravene, men bare for 10% av bankens totale innvilgede lån (8% i Oslo). Det betyr f.eks. at det teoretisk sett er mulig for en student å få avdragsfrihet på boliglånet sitt selv om den er belånt med mer enn 60%, dersom banken velger å gjøre avvik. Det som dessverre har vist seg i praksis er at avvikene “brukes opp” av de som kanskje egentlig ikke trenger det (men som bankene anser som lønnsomme kunder).

Implikasjoner og måter å tilpasse seg forskriften

Særlig for unge boligkjøpere representerer boliglånsforskriften noen hinder foran boligdrømmen, men det finnes flere måter å tilpasse seg dette kravet. Det har blitt veldig vanlig at foreldrene bidrar, og de fleste av tipsene i dette avsnittet vil derfor involvere foreldrehjelp (kan naturligvis være andre slektninger eller venner for den del). Hvis du er en mor eller far som ønsker å hjelpe din unge lovende, anbefaler jeg deg å tenke nøye gjennom hva du gjør, og hvordan du faktisk ønsker å bidra.

Banken har i utgangspunktet ikke mulighet til å tilby mer enn 85% belåningsgrad. Belåningsgrad er altså gjeld i forhold til boligens verdi (gjeld delt på boligverdi = belåningsgrad). Med andre ord kan ikke banken tilby lån til mer enn 85% av boligens verdi i henhold til boliglånsforskriften. Som nevnt tidligere kan man diskutere hva som er “forsvarlig verdivurdering”, men i de aller fleste tilfeller er dette lik kjøpesum eller prisantydning. Du må altså ha minimum 15% egenkapital for å kjøpe bolig. Mange velger å løser de siste 15% med at de tar sikkerhet i en annen bolig, eksempelvis dine foreldres bolig – såkalt tredjemannspant. Dine foreldre blir da realkausjonister. Alternativt kan man få noen til å stå som personalkausjonist, som jeg skal forklare i neste avsnitt. Et annet alternativ er et lån på privat hånd, f.eks. ved at man inngår en (skriftlig) låneavtale med foreldrene.

Banken har heller ikke lov til å innvilge lån på mer enn 5 ganger bruttoinntekten din. Har du 500.000 i bruttoinntekt kan du låne totalt 2.500.000. Dersom du trenger å låne mer kan dette løses ved at du får en av eller begge foreldrene dine (eller du kan finne deg en kjæreste med grei inntekt…) til å stå som medlåntaker. At en person står som medlåntaker betyr at den personen er ansvarlig for hele lånet, sammen med hovedlåntaker. Begge er solidarisk ansvarlig for hele lånet, som betyr at begge har samme ansvar for at lånet blir tilbakebetalt. En kausjonist, som jeg nevnte i forrige avsnitt, har derimot kun subsidiært ansvar, som betyr at kausjonistens ansvar for å tilbakebetale inntreffer etter at hovedlåntakeren ikke klarer å betjene lånet. En kausjonist kan hefte for hele eller deler av lånet, med hele sin ubeheftede formue og sin løpende inntekt. Dersom låntakeren misligholder lånet, kommer banken til kausjonisten. Dersom du ikke kan betale heller, kan banken begjære utleggspant i dine eiendeler for å dekke kravet. Dersom man har medlåntaker på lånet kan samlet inntekt legges til grunn, og det kan derfor løse inntektsproblemet som særlig unge låntakere har.

Begrepene medlåntaker og kausjonist brukes ofte om en annen, noen ganger feilaktig. Grunnen til det kan være så enkelt som at “kausjonist” ikke er definert i lovverket. Det avgjørende for om noe skal betegnes som kausjon, vil være om avtalen har et slikt formål og slike økonomiske virkninger som er typisk for kausjon. Slik sett kan det tenkes at en person som i praksis har signert på lånet som medlåntaker, egentlig er kausjonist, dersom det i realiteten er slik at deres ansvar for lånet kun blir aktuelt dersom hovedlåntakeren ikke gjør opp for seg (subsidiært ansvar). Dette er kanskje tilfelle for mange foreldre som hjelper sine barn inn på boligmarkedet. Likevel er det viktig å merke seg det juridiske solidaransvaret.

Topplån
Noen banker oppgir en rente for boliglån på inntil en gitt prosent av boligens verdi (typisk 70-75%). For den delen av lånet som overstiger dette kan man oppleve å måtte betale en høyere rente. Den andelen som overstiger (f.eks.) 75% kalles ofte topplån. Årsaken til at denne delen av lånet kan være priset høyere, er at både risikoen og fundingkostnaden for banken kan være høyere for den delen av lånet som overstiger 75%.

Det er ikke alle banker som oppererer med topplån, og de fleste store banker har en egen prisstrategi for unge boliglånskunder som gir dem samme rente på hele boliglånet, selv om det overstiger 75% av boligens verdi.

Mer om topplån for den som er spesielt interessert:
Jeg skrev jo tidligere at mange boliglån blir finansiert gjennom boligobligasjoner. Har du boliglån i Sparebank 1, vil du se (i lånedokumentene) at det ikke er utlånt av Sparebank 1, men av Sparebank 1 Boligkreditt. Sparebank 1 Boligkreditt utsteder boligobligasjoner som finansierer Sparebank 1-bankene sine boliglån – men bare inntil 75% av boligens verdi. Dersom du har lånt mer enn 75% av boligens verdi, vil du se at den delen av lånet som går over 75% er utlånt av Sparebank 1. Den delen av boliglånet ditt som er over 75% har banken altså finansiert på en annen måte (f.eks gjennom kundeinnskudd eller annen markedsfinansiering), og nettopp derfor kan disse lånene koste mer – i tillegg til at risikoen blir høyere når belåningsgraden går opp.

Refinansiering av boliglån
Refinansiering av boliglån er ganske greit. Med refinansiering mener jeg enten at man flytter lånet sitt fra en bank til en annen (tar opp nytt lån i ny bank, som innfrir lånet i din gamle bank), eller at man gjør endringer i eget boliglån i banken man har det i (f.eks øker boliglånet man allerede har). Som nevnt tidligere kan det etableres pant i en bolig du allerede eier, så det er ikke noe problem å ta opp nytt lån med sikkerhet i boligen din selv etter du har kjøpt den. Det er derfor mulig å søke om opplåning på bolig, eller for den del flytte lånet dersom en annen bank gir deg bedre vilkår. Etableringsgebyrer og tinglysningegbyrer påløper gjerne, så det bør du tenke over før du lar deg lokke over til en annen bank av bare 0,01% bedre rente.

Rammelån
Rammelån (også kalt boligkreditt eller fleksilån) er et flesibelt lån med sikkerhet i bolig, med mulighet for å utsette avdrag. Et rammelån kan gjøre det lettere å bruke boligformuen som sikkerhet for kjøp av varige konsumgoder, som f.eks. bil og båt. Du kan søke om rammelån på inntil 60% av boligens verdi. I dette ligger det at du kun kan søke om rammelån dersom boligen din er belånt med under 60%. Du betaler kun renter på den andelen du faktisk har belånt. Med andre ord, om du har en bevilget ramme på 500.000, men har benyttet bare 100.000 av rammen, betaler du bare rente på de 100.000.

Rammelån er noe det har blitt mer av ila de siste ti årene. Rammelån utgjorde bare 2% av samlet gjeld i 2005, og var opp i 14% i 2016.

Avdragsfrihet
Avdragsfrihet betyr at man i perioden avdragsfriheten gjelder kun betaler renter på lånet. Det er viktig å huske at etter en periode med avdragsfrihet på et nedbetalingslån vil terminbeløpene (rente + avdrag) være høyere enn før perioden startet, ettersom restgjelda er den samme men det gjenstår færre terminer å fordele avdragene på.

I henhold til boliglånsforskriten §7 kan avdragsfrihet kun avtales dersom boligen er belånt med under 60% av boligens verdi.

Billån

Billån er et lån med sikkerhet i bilen. I motsetning til boliglån er billån salgspantlån. Som nevnt tidligere innebærer det at det kun kan etableres sikkerhet i kjøretøyet i forbindelse med et reelt salg. Du kan derfor ikke søke om billån til en bil du allerede eier eller har bruksrett i. Det betyr også at du ikke kan kjøpe bil av noen som bor på samme adresse som deg med billån, da det ikke anses som et reelt salg. Dette byr på problemer når fraskilte skal “kjøpe ut” den andre fra bilen. Da kan man i utgangspunktet ikke få billån, ettersom begge allerede har bruksrett i bilen. Dersom begge står på lånet i utgangspunktet, kan imidlertid den ene fraknyttes lånet (som regel mot et lite gebyr). Da kan den ene parten fortsette å betale ned lånet alene, uten at den andre blir heftende for lånet.

En annen implikasjon ved at salgspant ikke kan etableres i en bil du allerede eier, er at dersom du har billån i en bank, kan ikke dette flyttes til en annen bank ved at den andre banken etablerer nytt salgspant. Noen banker (f.eks. Sbanken) sier at de tilbyr seg å flytte billånet. Dette forutsetter imidlertid at banken du har billån i idag tillater seg å overføre det eksisterende salgspantet. Det finnes ikke noen god infrastruktur for flytting av salgspant. Det er en manuell oppgave som er ressurskrevende og som ofte medfører mye krøll med salgspantet. Mange banker reserverer seg derfor mot å flytte salgspant.

De fleste banker tilbyr billån med inntil 100% finansiering. Slik som med boliglån vil du kunne forvente deg en bedre rente hvis du har egenkapital, enn hvis du ikke har det. Som regel får man den beste billånsrenten hvis du har 35%-50% egenkapital eller mer. Igjen har dette med bankens sikkerhet å gjøre. Selv om banken har sikkerhet i bilen din, betyr ikke det at du kan forvente å få samme rente på billån som på boliglån. En bolig stiger gjerne i verdi, mens en bil typisk synker i verdi. Det er derfor to helt ulike risikoer knyttet til bolig og bil. Bolig er typisk ansett som et investeringsobjekt, mens en bil typisk anses som noe vi konsumerer.

Refinansiere billån
Av de årsakene som jeg har nevnt tidligere lar det seg altså ikke gjøre å refinansiere billån. Det kan derfor være ekstra lurt å ta en runde ekstra når du kjøper bil, for å se at du er i en bank du vil ha lånet i gjennom hele løpetiden på lånet, og at du har en nedbetalingstid som gir et terminbeløp du kan leve med. Dersom du eier bolig kan du eventuelt ta opp et ekstra lån med sikkerhet i boligen din for å innfri billånet, og på den måten “refinansiere” det.

Valg av nedbetalingstid
Du bør ikke velge en nedbetalingstid som er lengre enn den tiden du tenker å eie bilen. Særlig gjelder dette dersom du fullfinansierer bilen (0% egenkapital). Ettersom billån normalt er annuitetslån, betyr det at andelen av terminbeløpet som er avdrag er mye lavere i starten av låneperioden enn mot slutten. Det betyr at halvveis ut i låneperioden har du fremdeles mer enn halvparten av lånet igjen. Dersom du da ønsker å selge bilen, og den har tapt seg mer i verdi enn det du har betalt ned på lånet, vil du måtte punge ut for mellomlegget. Du kan ikke fortsette å betale på billånet ditt etter bilen er solgt. I noen tilfeller kan banken gjøre om resten av lånet til et forbrukslån, men det er jo ganske kostbart.

Sammenligne billån
Når du sammenligner billån, må du sammenligne den effektive renten. På billån legges gebyrene til på lånebeløpet, og nedbetales over hele løpetiden. Det betyr at dersom du låner 100.000 kroner til kjøp av bil, og etableringsomkostningene er 4.000 kroner, blir det totale lånebeløpet 104.000 kroner som nedbetales over valgt løpetid. I tillegg kommer termingebyr hver måned. Min erfaring er at mange bilforhandlere og små finansieringsselskaper lokker til seg kunder med lave nominelle renter, men har høye gebyrer. Kundene lar seg lure til å tro at tilbudet de har fått fra forhandler er bedre enn det de fikk i banken sin, fordi den nominelle renten er lavere. Totalkostnaden på lånet blir imidlertid ofte høyere pga de høye gebyrene. Sammenlign derfor alltid den effektive renten, og vær kritisk til de tilbudene du får fra bilforhandler. Husk at de får provisjon når de selger deg lån. De har ingen motivasjon (eller kompetanse) til å gi deg god finansiell rådgivning.

Husk at den effektive renten også avhenger av lånebeløpet og løpetiden, som nevnt tidligere. Et lavt lånebeløp vil ha høyere effektiv rente enn et høyt lånebeløp, alt annet likt. Dette fordi gebyrene blir en større del av totalkostnaden på lånet ved et lavt lånebeløp enn ved et større lånebeløp.
Kort nedbetalingstid betyr at effekten av etableringsgebyret blir større på den effektive renten enn ved lang nedbetalingstid (flere år å fordere kostnaden på)

Tinglysningsomkostningene er det staten som tar, og er derfor ikke gjenspeilet i den effektive renten på billånet.

Kan forbrukslån være bedre enn billån?
Dersom du skal kjøpe en billig bil, og absolutt skal lånefinansiere den, kan du komme bedre ut ved å ta et forbrukslån. Årsaken er at du da slipper tinglysningsgebyret, og etableringskostnadene er som regel mye lavere. I tillegg er det slik at dersom du har et lån med sikkerhet i bilen, krever banken som regel at du har kaskoforsikret den. Det gir for de fleste lite økonomisk mening å kaskoforsikre en bil som koster 30.000 kroner. Dersom du tar et forbrukslån stiller ikke banken noe krav til kaskoforsikring, og du kan forsikre den med delkasko eller enkel ansvarsforsikring – som er vesentlig billigere.

Jeg prøvde meg i en lånekalkulator i en stor norsk bank, og fant at et billån på 30.000 kroner over 2 år ga en månedskostnad på 1.510. I tillegg kommer altså kostnader knyttet til dyr forsikring. Et forbrukslån på samme størrelse i samme bank over 2 år ville koste meg 1.471 i måneden.

Grunnen til at effektiv rente er høyere på forbrukslånskalkulatoren, selv om månedsbeløpet er lavere, er at tinglysningsomkostningene på billånet ikke er reflektert i den effektive renten, men er inkludert i terminbeløpet. Logikken bak det er at terminbeløpet ikke er en lånekostnad som sådan, men en avgift til Brønnøysundregistrene for tinglysning av salgspantet.

Men altså, skal du kjøpe en bil til 30.000 kroner – spar opp litt penger da vel…

Forbrukslån

Forbrukslån er lån uten sikkerhet. En av de vanligste formene for forbrukslån er det vi pådrar oss ved å bruke kredittkort. Selve ordet forbrukslån er et ord som gir mange en dårlig smak i munnen, og som gjerne er forbundet med en del skam og angst – kanskje på grunn av programmer som Luksusfellen. Luksusfellen viser at vi i dagens samfunn er, bokstavelig talt, bare noen få klikk unna kreditt, og når økonomien plutselig kollapser, så kollapser den gjerne “big time”.

Forbruklån er ikke nødvendigvis bare for idioter. Problemet er at også idioter har forbrukslån. Et forbrukslån kan være helt stuerent det, så lenge du har kontroll på økonomien din. Merk at når jeg sier forbrukslån, mener jeg ikke at man bruker kredittkortet sitt, og betaler alt når regningen kommer. Dette kan jo være beint fram smart hvis du får rabatter eller bonuspoeng ved bruk av kredittkort, og betaler tilbake før det begynner å løpe renter på lånet. I mine øyne er det ikke forbrukslån før det begynner å løpe renter.

Gjennomsnittlig lånerente for husholdninger i dag er på rundt 3%. Renten på forbrukslån ligger på rundt 12-25%, og forbrukslånsbankene tjener derfor veldig mye penger (Bank Norwegian er jo verdt mer enn flyselskapet). Det er lett å se at en slik høy rente vil gi en veldig høy rentebelastning for de med høye forbrukslån. Veksten i forbrukslån har økt de siste årene, og selv om forbrukslån utgjør en relativt liten andel av samlet gjeld (ca 3%) utgjør de en relativt høy andel av husholdningenes renteutgifter (ca 12%). Misligholdsraten (andel av totale lån som misligholdes) på forbrukslån er også vesentlig høyere enn andre typer lån, og høyest andel mislighold ser vi blant de under 30 år.

Jeg spurte helt innledningsvis hvorfor vi egentlig låner penger, og svaret var at vi gjør det for å flytte konsum fra fremtiden til i dag – og da må vi flytte penger fra fremtiden til i dag. La oss anta at du er student med en inntekt på 10.000 per måned, og du står overfor følgende dilemma (inspirert av Helge A Nordahl ved OsloMet):

Kjøpe oppvasmaskin i dag med forbrukslån, eller spare og kjøpe oppvaskmaskin etter 3 måneder?
Vi antar at oppvaskmaskinen koster 6.000. Ved å ta et forbrukslån, vil vi ha litt mer å bruke på konsum de første tre månedene enn ved alternativet, ettersom vi ikke behøver å spare, men fra og med måned 4 vil konsumet være lavere fordi vi fremdeles må betale ned kredittkortgjelden.

Måned	Spare	Kjøpe på kreditt
1	8000 (vasker for hånd)	9400 (oppvaskmaskin)
2	8000 (vasker for hånd)	9400 (oppvaskmaskin)
3	8000 (vasker for hånd)	9400 (oppvaskmaskin)
4-12	10000 (oppvaskmaskin)	9400 (oppvaskmaskin)

Dette oppsettet i seg selv vil ikke gi et entydig svar. Det som betyr noe er: hva er nytteverdien ved de ulike alternativene? Hvor mye verdsetter du å kunne leve litt bedre i måned 1-3 selv om det medfører lavere forbruk enn alternativet i måned 4-12? Hvor mye verdsetter du å kunne slippe å ta oppvasken for hånd i måned 1-3? Hvor mye verdsetter du et jevnt konsum, som jeg skrev om innledningsvis.

Med andre ord, forbruklån kan være greit hvis du anser at nytten av fremskyndet konsum overstiger kostnaden knyttet til det. Dessverre er det mange der ute som er dårlige på å beregne både nytte og kostnad, og ender opp med store forbruklån som de ikke makter å betjene til et konsum de strengt tatt ikke har noe nytte av…

Jeg anbefaler på ingen måte forbrukslån, men jeg ville trekke frem poenget over okke som. Jeg tenker slik at det må være greit å ta opp kortsiktig gjeld til kortsiktige formål (som å slippe å vaske for hånd i tre måneder), men det bør koste, og det bør være vanskeligere å få tak i enn det er i dag – for å redusere etterspørselen etter kortsiktige lån. Stadig flere unge tar opp kortsiktige lån, fordi det er lett tilgjengelig. Andelen forbrukslån og, enda verre, misligholdsraten på forbrukslån er urovekkende høy blant unge mennesker. Det kan nesten virke som om noen har mistet helt begrepet om hva penger er, og hvilke forpliktelser et lån faktisk innebærer. Jeg skal i et senere innlegg på bloggen skrive om hva hvordan betalingsproblemer oppstår, og hva som skjer når man misligholder et lån.

Hva innebærer egentlig rentefrie dager på kredittkort?
Denne banken tilbyr inntil 45 dager rentefri kreditt. Hva betyr egentlig det? Dette er noe som forvirrer kortholdere i alle aldre, så her skal man ikke føle seg dum selv om svaret er ganske enkelt. Når man kjøper en vare med kredittkort, så kommer dette kjøpet på neste faktura. Det begynner ikke å løpe renter på dette beløpet før etter den fakuturaen har forfalt. La oss anta at du har forfall den 14. per måned. Fakturaen produseres 14 dager før forfall, altså den 1. hver måned. Den 1. januar produseres fakturaen for januar. Du kjøper en vare senere på dagen den 1. januar. Denne transaksjonen vil komme på fakturaen den 1. februar, og den fakturaen vil ha forfall 14. februar. Det vil si at du har hele januar (31 dager), pluss 14 dager frem til fakturaen forfaller 14. februar. Til sammen har du da 45 dager før rentene begynner å løpe. Merk at det står inntil 45 dager. Det betyr at dersom du kjøper varen den 31. desember, så vil denne transaksjonen komme på fakturaen som produseres 1. januar, og du vil kun ha rentefri periode frem til 14. januar (15 dager).

Fast eller flytende rente?

Si det…
Fast rente eller flytende rente er et valg man i avisene ofte blir pushet til å ta stilling til. Kalkylen for rente har vi allerede vært gjennom, og den er forsåvidt helt lik for fastrente og flytende rente, men det er fundingkostnaden til banken som vil utgjøre forskjellen. Fundingkostnaden for banken vil være ulik for korte og lange lån, avhengig av hvordan forventningen er til renten fremover. Jeg skal forsøke å forklare veldig enkelt hvordan denne mekanismen fungerer. De som har over gjennomsnittlig kunnskap om rentekurver og terminpremier vil kanskje synes dette er litt for forenklet, men la gå.

Figuren vises to ulike rentekurver. En stigende kurve, og en synkende kurve. Rentekurven viser markedsrenten på lån med ulik løpetid. En flytende rente vil være det vi kaller en kort rente, mens en fastrente vil være det vi kaller en lang rente (hvor lang rente det er vil avhenge av hvor lang bindingstid vi har på lånet). Dersom markedet forventer at renten skal stige, har vi en stigende rentekurve. Dersom forventningene til renten fremover er at de skal synke, har vi en fallende rentekurve.

I teorien er det slik at fastrente skal være lik den forventede flytende renten i bindingsperioden. Det betyr at dersom man forventer en stigende rentekurve, vil fastrenten være høyere enn dagens flytende rente fordi snittet av renten de årene du har bundet renten vil være høyere enn renten i dag. Med andre ord skal det ikke spille noen rolle om du velger fast eller flytende rente – men dette er jo i teorien, og forutsetter at man vet helt nøyaktig hva de korte rentene vil være i fremtiden. I praksis vil det aldri være sånn – både fordi ingen kan spå fremtiden, og fordi at det alltid vil ligge et større eller mindre “risikopåslag” på lange renter som følge av denne usikkerheten. I Norge har vi ikke lange tidsserier for fast eller flytende rente, fordi renten historisk sett har vært veldig politisk bestemt, mens inflasjonsstyring av renten slik vi har i dag bare har eksistert siden rundt tusenårsskiftet. Vi har derfor ikke nok datagrunnlag for å si noe helt sikkert om det norske rentemarkedet. Ser vi over dammen, ser vi at flytende rente i det amerikanske rentemarkedet har vært lavere enn fastrente over tid.

Ved flytende rente kan banken foreta justeringer når som helst (låntaker blir varslet minimum 6 uker i forveien jfr finansavtaleloven med noen få unntak). På den annen side kan du som låntaker når som helst innløse lånet til pari kurs (lånebeløpet + påløpte renter på innløsningsdagen) dersom du har flytende rente.

Dersom du binder renten i form av et fastrentelån blir du som låntaker bundet til å betale rente for hele perioden rentebindingen gjelder (normalt 3, 5 eller 10 år). Banken kan på sin side ikke endre renten i perioden. Det betyr at dersom den flytende renten stiger til nivåer over fastrenten, vil du fremdeles ha samme fastrente. Du mister en del fleksibilitet ved å ha fastrentelån. Eksempelvis har du begrenset mulighet til å endre betalingsplan, gjøre ekstra innbetaling på lånet eller innfri lånet i sin helhet. Dersom du skal flytte, er det normalt uproblematisk å flytte fastrentelånet over til ny bolig.

Dersom du velger å bryte fastrenteavtalen beregnes en overkurs (dersom markedsrenten er lavere enn fastrenten din) eller en underkurs (dersom markedsrenten er høyere enn fastrenten din). Overkursen må du betale til banken for å kompensere for at banken nå må låne ut pengene til en lavere rente enn det de ville fått av deg dersom du opprettholdt din fastrenteavtale. Underkurs oppstår fordi banken har en fordel ved at fastrenteavtalen brytes, slik at de kan låne ut pengene til andre til en høyere rente. Denne underkursen skal fortrinnsvis komme til fratrekk på din restgjeld. Hvordan over- og underkurs beregnes tenker jeg er for teknisk for dette innlegget.

Det er ikke noe entydig svar på om man skal velge fastrente eller flytende rente. Det blir en beslutning du må ta. Kanskje betaler du i sum noe mer i rente ved å velge fastrente, men du kan se på det som en forskringspremie du betaler for å sikre deg mot plutselig økning i rentenivået. Det blir litt som å betale innboforsikring. Sannsynligvis brenner ikke kjøkkenet ditt ned, men hvis det gjør det, er det utrolig greit å være forsikret. Hvor mye verdsetter du forutsigbarhet? Har du økonomi til å tåle eventuelle svingninger? Det man også kan tenke på er at den flytende renten, som nevnt, er knyttet til pengemarkedsrenten, som igjen er veldig tett knyttet til styringsrenten. Styringsrenten settes av Norges Bank, og er som regel lav i dårlige tider (for å få igang økonomien) og høy i gode tider (for å bremse økonomien). Det betyr at du kan forvente lav flytende rente i tider hvor økonomien går treigt, og økonomien i husholdningen kanskje er dårlig, og høy rente i periodene hvor du uansett har ekstra til overs før renter. Det kommer jo an på hva du driver med. Kanskje er din husholdnings økonomi god når det går dårlig for andre og omventdt…

Du kan jo også sikre deg ved velge å ha fastrente på deler av lånet, og flytende rente på resten. For den som har kjennskap til porteføljeteori, er ikke dette valget så dumt valg for de fleste husholdninger ettersom man får spredt risikoen litt. I Norge er det relativt få som har fastrente på boliglån, i motsetning til mange andre europeiske land. Årsaken kan være så enkel som at man i Norge har flytende som standard, og at husholdningene derfor må gjøre et bevisst valg ved å endre til fastrente. I andre land, som f.eks. Tyskland, er fastrente standarden, og man må gjøre et bevisst valg på å bytte til flytende rente. Vi vet at folk har en tendens til å gjøre som flertallet gjør, så det kan jo være en forklaring. Vi ser i disse dager en økning i andel fastrentelån i Norge, noe som kan skyldes at rentenivået på fastrente er veldig lavt, noe som gjør nedsiden ved fastrente relativt liten.

Serielån og annuitetslån

De fleste av dere økonomistudenter kan forhåpentligvis hoppe over denne biten.

De vanligste formene for nedbetalingsplan heter serielån og annuitetslån. Annuitetslån har en nedbetalingsplan som gir et helt likt terminbeløp (sum av rente og avdrag) hvert termin. I starten vil man betale mest rente, mens terminbeløpet mot slutten stort sett består av avdrag. Serielån har en nedbetalingsplan som gir en helt lik avdrags-del hvert termin, mens rentebeløpet vil variere fra termin til termin ettersom man hele tiden betaler rente av restgjelden på lånet. Man vil i starten av lånets løpetid derfor betale mer på et serielån per termin enn man gjør i de siste terminene.

Annuitetslån og serielån (Finanssans.no)

Hva er mest gunstig? Vel, det er ikke slik at det ene er bastant mer gunstig enn det andre. Noen vil si at et annuitetslån er dyrere, fordi vi betaler mer renter i kroner og øre, men det er jo bare rett og rimelig, ettersom vi låner mer penger lengre (lavere avdrag i starten enn ved serielån). Da må man jo også betale mer i renter i kroner og øre. Likevel velger de fleste annuitetslån, ettersom man da har et lavere terminbeløp i starten enn med serielån. Særlig unge som låner penger vil velge annuitetslån fordi de har en økonomi i dag som gjør et lavere terminbeløp mer attraktivt. Dessuten mener vi jo at det er mer verdt å ha litt ekstra til overs i dag, enn å vite at vi får litt ekstra til overs om noen år…

Til slutt vil jeg si at jeg håper dette innlegget har vært opplysende, uansett om du har lest hele eller bare deler av det. Har du noen spørsmål eller innspill ser jeg frem til å lese dem i kommentarfeltet.