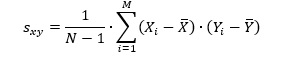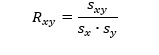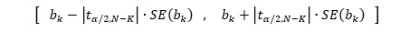Første arbeidskrav i metode og økonometri er ute, og kanskje har dere allerede bestått med glans. For de som ikke har det: la oss finne ut av dette sammen. Siden dere ikke har nummeret mitt, og ikke kan vippse meg penger, får dere heller legge igjen en kommentar hvis dere syns dette er et innlegg du setter over gjennomsnittet pris på (eller verdsettelse-strek som vi sier i dette faget, hehehehehehehehehehehe.) Har ikke orket å lese over innlegget, så si ifra hvis du finner noen feil også.
I dette arbeidskravet skal vi blant annet se på en rekke forhold på arbeidsplassen (uavhengige variabler) og hvordan de utgjør den samlede poengsummen (indeksen) som uttrykker hvor fornøyd de ansatte er med sjefen sin (Y).
I oppgave 1-10 i arbeidskravet har vi X uavhengige variabler (X2, X3… X7). Så det vi ønsker å finne ut fra en regresjonsanalyse er å finne ut f.eks hvor mye, og i hvilken retning, en endring i X2, som i vårt tilfelle er prosentandelen ansatte som mener sjefen ikke forskjellsbehandler de ansatte, påvirker Y (den avhengige variablen).
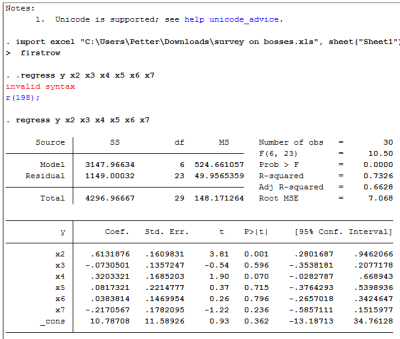
Det første jeg gjør er å importere excel-arket “survey on bosses” i Stata, og kjører en regress på modell (1). Dette gjør du ved å skrive “regress y x2 x3 x4 x5 x6 x7” i command-linja. Da kjører du en regresjon på modellen: Y = B1 + B2x2+B3x3… +B7x7 + u
I oppgave 1 skal vi finne den estimerte effekten på tilfredsheten med klage-håndtering. Det du må se etter da er B2, altså “Coef.” til x2. Den ser du er 0.6131876.
I oppgave 2 skal du ta utgangspunkt i beregningen til modell 1, og se hvilken av de 4 tolkningene som er korrekte. Spørsmålet er knyttet til x3, altså forskjellsbehandlingen. Her er det viktig å merke seg den negative sammenhengen mellom den uavhengige variablen x3 og den avhengige variablen. Det kan med andre ord se ut som at dersom antallet som mener sjefen ikke forskjellsbehandler stiger, så synker tilfredsheten noe (0,07305), gitt at de andre uavhengige variablene forblir uendret.
I oppgave 3 blir du bedt om å finne residualkvadratsummen (RSS – Residual Sum of Squares). Den finner du der det står “residual” og under SS. Altså 1149,00.
I oppgave 4 skal du også ta utgangspunkt i modell 1, og svare på hvor mye av variasjonene i indeksen for tilfredsheten med sjefen som forklares av modellen. Det er det vi kaller forklaringskraft, og den regnes ut ved (1 – (RSS/TSS)). RSS fant du i oppgave 3, og TSS er “total”, altså 4296,96667. Den er også regnet ut i modellen. Da må du se på R-squared. Den sier 73,26%.
I oppgave 5 skal vi se på generell tilfredshet på jobben. De variablene som har med de ansattes forhold til sjefen å gjøre basert på generell tilfredshet er x2, x3 og x6. Derfor må du kjøre en regress på de variablene. Da får du en ny RSS (RSSmed) som er 1361,80481. RSSuten har du fra før, for den fant du i oppgave 3.
Så bruker du denne formelen for å finne testobservator: ((RSSmed – RSSuten) / m) / ((RSSuten / (N – K )) hvor m er antall hypoteser/restriksjoner, N er antall observasjoner og K er koeffisienter i regresjonsmodellen (uten restriksjoner)
((1361,8004 – 1149 ) / 3) / (1149 / (30 – 7)) = 1,42
I oppgave 6 må du slå opp i tabellene på 1%, 5% og 10% signifikansnivå og se på m=3 og N-K = 23 for å se om noen av verdiene der er lavere enn 1,42. Er de lavere, forkastes nullhypotesen. Jeg får henholdsvis verdiene 4,76, 3,03 og 2,32. Ingen av dem er lavere enn 1,42, som betyr at nullhypotesen ikke forkastes på noen av de tre signifikansnivåene.
I oppgave 7 gjør du samme prosess, men med X2, X3 og X6 satt lik null, slik at du kjører regress på X4, X5 og X7
((RSSmed – RSSuten) / m) / ((RSSuten / (N – K ))
((1923,42417 – 1149) / 3) / (1149 / 23) = 5,17
I oppgave 8 sjekker du tabellene igjen, og ser om noen av verdiene er lavere enn 5,17. Igjen, jeg får henholdsvis verdiene 4,76, 3,03 og 2,32. Alle av dem er lavere enn 5,17, hvilket betyr at nullhypotesen forkastes ved alle de tre signifikansnivåene.
I oppgave 9 kjører du en regress på bare x2.
((1369,38241 – 1149) / 5) / (1149 / 23) =0,882
Sjekker du m=5 N-K =23 i tabellen får du henholdsvis 3,94, 2,64 og 2,11. Ingen av dem er lavere enn testobservatoren – ergo nullhypotesen forkastes ikke hvis vi bruker et signifikansnivå som er 10% eller lavere.
I oppgave 10 mener jeg det er åpenbart at man bør iverksette tiltak som bedrer sjefens håndtering av ansatteklager, ettersom vi ikke kan forkaste hypotsenen om at dette alene betyr noe for tilfredsheten med sjefen.
I oppgave 11 skal du finne utvalgskovariansen mellom NO2 og CAR. Vi vet at utvalgskovariansen finnes slik:
Men, vi kan også finne den ved å snu om på formelen for utvalgskorrelasjon (som vi har fått oppgitt).
Sx og Sy (Sno2 og Scar) er kvadratrota av de to variansene.
034 = X / rot(1903,84) * rot(1,31)
0,34 = X /43,6330 * 1,1445523
0,34 = X / 49,94
X = 16,98
Oppgave 12: Med utgangspunkt i denne informasjonen kan vi beregne modellen: NO2 = B1 + B2CAR + u slik:
For å beregne B2 bruker du B2 = Cov(CAR,NO2) / Var(CAR). Cov fant du i forrige oppgave. Variansen er gitt i den innledende oppgaveteksten (1,31)
16,98/1,31 = 12,96CAR
Deretter finner du B1 ved:
B1 = NO2-strek – B2*CAR-strek | hvor jeg med strek mener gjennomsnitt (som er gitt i innledende oppgavetekst)
Altså B1 = 52,11 -12,96*1,63 = …
I oppgave 13 skal du finne R^2. Du har oppgitt R (utvalgskorrelasjonen), så bare opphøyd den i andre.
I oppgave 14 skal du finne justert determinasjonskoeffisient
Den finner du ved: 1-(1-R^2) * ((N-1)/(N-K)) | hvor
Med andre ord:
R^2justert = 1- (1-0,1156) * (63-1) / (63-2) = …
I oppgave 15 skal du bruke modellen du laget i oppgave 12 til å beregne NO2 for 1,63CAR. Da bare legger du inn verdien 1,63 slik at du får
30,99 + (12,96*1,63) = …
I oppgave 16 skal du regne konfidensintervallet. Du vet at stigningstallet er 12,96 jfr oppgave 12. Bruk den som bk i formelen:
Bruk tabell for t-fordeling (60 frihetsgrader) Da burde du få noe slikt:
[12,96 – (2,00*4,59) , 12,96 + (2,00*4,59)]
Regn ut, og finn rett svar!
I oppgave 17 går jeg inn i tabellen, på 18 frihetsgrader, og ser at 1,330 ligger på 20%, altså er svaret 80% sannsynlighet for at testverdien ligger i intervallet.
I oppgave 18 blir løsningen slik:
Testverdi = B2 – H0-verdi / se(b2)
Testverdi = 1,26 – 1 / 0,20
Testverdi = 1,3
I oppgave 19 slår vi opp i tabellen på 40 frihetsgrader ( fordi vi har 2 B-er, dvs k=2, og frihetsgrader er (n-k) = 42-2=40.
Vi finner 1,3 på 20%.
I oppgave 20 må vi forstå hvordan vi finner ut antall Xer. Antall Xer er én mindre enn antall Ber. Antall B-er uttrykkes som k, og frihetsgrader uttrykkes som n-k
Med andre ord får vi nok en ligning her. Jeg stikker mitt usedvanlig velstelte ansikt inn i tabellen for en ensidig test (fordi her har vi bare én side, vi skal sjekke om B2 er større enn null). Jeg finner ut at med 5% signifikansnivå er 23 frihetsgrader gir vår kritiske verdi på 1,714. Det vil altså si at:
n-k = 23
n er gitt som 27 som gir oss en sjukt i hue jævlig enkel ligning:
27-k = 23
k=4
Som jeg sa var k lik antall B-er, og antall Xer er (k-1)
4-1 = 3 skulle jeg mene.
Gratulerer. Du har nå bestått arbeidskrav 1 med 100% riktige svar.
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen