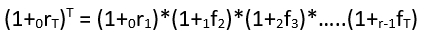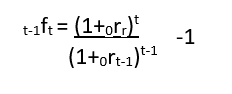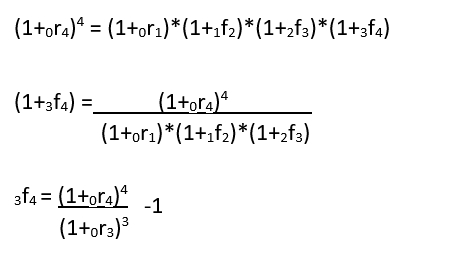Som dere kanskje har lagt merke til på It´s Learning er det blitt lagt ut en test til faget finansiell styring. Jeg har løst det, og tenkte å dele det her for de som vil sjekke svarene sine, står fast eller bare vil skjønne mer om hvorfor det blir som det blir.
Oppgave 1
Et selskap skal opprettes med en startkapital på 6 millioner kroner. Ledelsen vurderer å finansiere selskapet ved hjelp av 120 000 aksjer til kurs 30 kroner pluss gjeld til 5 % rente. Ledelsen regner med at selskapet vil få et driftsresultat før renter på 360 000 kroner med sannsynlighet på 1/3 og på 900 000 kroner med sannsynlighet på 2/3. Se bort fra skatt.
a) Hva er det forventede overskuddet per aksje?
1/3 sannsynlighet for driftsresultat før renter på 360.000
2/3 sannsynlighet for driftsresultat før renter på 900.000
Forventet OFR (Overskudd Før Renter):
E(OPR) = (360.000*1/3) + (900.000*2/3) = 120.000 + 600.000 = 720.000
Lånebeløpet må være differansen mellom startkapitalen på 6.000.000 og den egenkapital som blir innskutt gjennom utstedelse av aksjer.
Lånebeløp = 6.000.000 – (120.000*30) = 2.400.000
Rente:
2.400.000*0,05 = 120.000
Forventet OER (Overskudd Etter Renter)
[OFR – renter]
720.000 – 120.000 = 600.000
Forventet OPA (overskudd pr aksje):
[OER/antall aksjer]
600.000/120.000 = 5 kroner
b) Hva er standardavviket til forventet overskudd pr. aksje?
Standardavviket er kvadratrota til variansen:
Sannsynligheten er 1/3 for et OPA på (360.000-120.000)/120.000 = 2
Sannsynligheten er 2/3 for et OPA på (900.000-120.000)/120.000 = 6,5
Her ser du at du kunne funnet forventet OPA ved å ta
(1/3*2) + (2/3*6,5) = 5
Varians:
1/3*(2-5)^2 + 2/3*(6,5-5)^2
= 3 + 1,5
= 4,5
Standardavviket er kvadratrota av 4,5, altså 2,12
c) Hva er det som måles med standardavviket til forventet overskudd per aksje? Bruk maks. 3 linjer på svaret.
Standardavviket er en måte å måle spredningen i fordelingen over mulige avkastninger i et prosjekt/investering. Standardavviket til forventet OPA er derfor en måte å måle usikkerheten (risikoen) til eierne på.
Ledelsen bestemmer seg for å finansiere selskapet med bare egenkapital.
d) Hvor mange aksjer må selskapet utstede til kurs 30 kroner per aksje?
Hvor mange aksjer må selskapet utstede til kurs 30 kroner for å få dekket kapitalbehovet på 6.000.000 kroner?
30*X=6.000.000
X= 200.000 aksjer
e) Hva er det forventede overskuddet per aksje når selskapet er 100% egenkapitalfinansiert?
Vi kan se to åpenbare konsekvenser av at selskapet velger å finansiere selskapet med bare egenkapital:
1. Antall aksjer stiger (som vil påvirke resultatet per aksje negativt, ettersom vi får et større tall i nevner)
2. Rentene bortfaller (som vil påvirke resultatet per aksje positivt, ettersom vi får et større tall i teller)
Forventet OFR har vi allerede regnet ut
(360.000*1/3) + (900.000*2/3) = 120.000 + 600.000 = 720.000
Ettersom vi ikke har noe renter, blir jo dette det endelige overskuddet. Vi deler dette på det nye antallet aksjer.
Da får vi OPA = 720.000/200.000 = 3,6
f) Vil standardavviket til forventet overskudd per aksje ved 100% egenkapitalfinansiering bli større eller mindre enn standardavviket til forventet overskudd per aksje i spørsmål b)? Begrunn svaret.
Bruk maks. 5 linjer på svaret. (Du trenger ikke å regne.)
Dersom det finnes investeringsrisiko, det vil si at det er mer enn 1 mulig utfall for OFR (slik som i denne oppgaven) vil en positiv gjeldsgrad påføre eierne finansieringsrisiko. Risikoen i forventet overskudd per aksje øker med gjeldsgraden. Ettersom standardavvik er et mål på risiko, og et høyere standardavvik betyr høyere risiko, vil standardavviket til forventet overskudd per aksje ved 0% gjeld (100% EK) være mindre enn standardavviket til forventet OPA ved mer enn 0% gjeld. Vi ser at forventet OPA er 5 kroner når vi har gjeld, og bare 3,6 uten gjeld. I sum over tid sier vi at en høyere risiko skal kompenseres med en høyere avkastning, og vise versa. Vi ser dette også ved å sammenligne utfallsrommet i oppgave e) med det i oppgave b). som Utfallsrommet i e) er 4.50-1.80=2.70. Utfallsrommet i b) er: 6.50-2.00=4.50 – altså større.
Oppgave 2
Noran ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 28 millioner kroner årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 14 %, risikofri rente er 3 %, og forventet risikopremie er 6 %. Noran opptar nå gjeld for 100 millioner kroner til markedsrente på 5 %. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad (gjeld/egenkapital) regnet til markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og se bort fra skatt.
a) Hvordan påvirkes selskapets totalkapitalkostnad av refinansieringen?
Jeg tenkte å si hva som menes med “M&M-forutsetningene”:
Forutsetningen for perfekt kapitalmarked innebærer følgende:
– Alle investorer har full informasjon om mulighetene i markedet.
– Alle kan låne til samme rente og med samme risiko, og det er ingen transaksjonskostnader.
– Egenkapitalen i selskapene er fritt omsettelig (aksjer og obligasjoner)
Miller og Modigliani (M&M) tar videre flere forutsetninger enn det som ligger i definisjonen av det perfekte kapitalmarked for å kunne finne verdien av selskaper innenfor samme risikoklasse. De forutsetter at for et gitt selskap vil sannsynlighetsfordelingen til overskudd før renter (OFR) være den samme i alle perioder. Videre antas OFR evigvarende og gjeldsgrad konstant over tid. Miller og Modigliani antar også at overskuddet i sin helhet betales ut som utbytte til eierne. Forventningsverdien til OFR og kontantstrømmen til kreditorer og til eiere blir derfor som uendelige annuiteter å regne.
Basert på disse forutsetningene kan vi si at:
Kapitalkostnaden til totalkapitalen = E(OFR)/V
hvor:
*E(OFR) er forventet overskudd før renter
*V er markedsverdien av selskapet (altså EK + gjeld)
Vi har fått oppgitt at egenkapitalkostnaden til selskapet før refinansieringen er 14%. Ettersom totalkapitalen utelukkende besto av egenkapital før refinansieringen, betyr det at totalkapitalkostnaden også var 14%. Dette er samme logikk som med totalkapitalrentabilitet og egenkapitalrentabilitet. Dersom man står overfor en bedrift som er 100% finansiert av egenkapital (ingen gjeld), vil totalkapitalrentabiliteten og egenkapitalrentabiliteten være like stor.
Dette kan vi kontrollregne, selv om det ikke er nødvendig:
[Kapitalkostnaden til totalkapitalen = E(OFR)/V]
Forventet OFR er jo 28 millioner. V, altså verdien av selskapet må være 200 millioner. Dette vet vi fordi selskapet har tatt opp et lån på 100 millioner, hvilket gir dem en G/E=1. Det betyr at ettersom G er 100 millioner, må også E være 100 millioner. V=totalkapitalen, altså G+E som må være 200 millioner.
Det gir oss:
28.000.000/200.000.000 = 0,14 etter refinansiering (og som vi så tidligere, vil ikke denne avhenge av finansieringen, så derfor er den 14% både før og etter refinansieringen.)
Oppsummert: Ettersom totalkapitalkostnaden er uavhengig av gjeldsgraden (med andre ord at finansieringsstrukturen ikke påvirker selskapets verdi) under disse forutsetningene, vil den forbli uendret etter refinansieringen.
b) Hva blir egenkapitalkostnaden etter refinansieringen?
I motsetning til totalkapitalkostnaden som er uavhengig av gjeldsgrad (G/E) er egenkapitalkostnaden økende ved økt gjeldsgrad. Dette skjønner vi når vi ser formelen for egenkapitalkostnad i M&Ms resultat nummer to:
Ke = Kt + (Kt – Kg)*G/E
Vi har allerede stadfestet at standardavviket, og derfor risikoen for eierne, øker når gjeldsgraden stiger. Uttrykket over viser hvordan dette påvirker egenkapitalkostnaden.
Så til oppgaven rent regneteknisk:
Da kan vi videre bruke flere formler. F.eks denne:
Ke = Kt + (Kt-Kg)*G/E
Ke = 0,14 + (0,14-0,05)*1
Ke = 0,23 = 23%
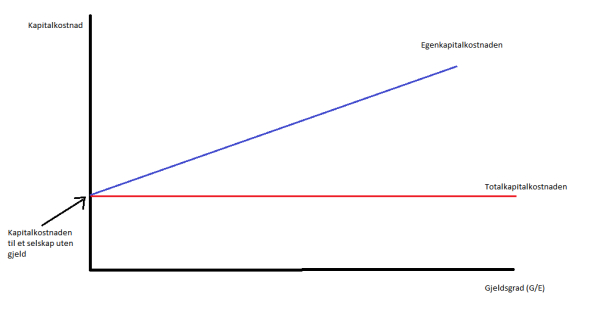
c) Kan du ved hjelp av en figur illustrere sammenhengen mellom totalkapitalkostnad og gjeldsgrad, og sammenhengen mellom egenkapitalkostnad og gjeldsgrad?
Ja, for dere kan jeg vel gjøre hva som helst:
Overstående figur gjelder altså for M&M sitt “univers” – uten skatt.
d) Hva er verdien av Noran når selskapet er 100% egenkapitalfinansiert?
Dette finner vi ved å ta overskuddet og dele på egenkapitalkostnaden (som for øvrig er lik totalkapitalkostnaden):
Markedsverdien av selskapet = V = 28.000.000/0,14 = 200.000.000
e) Hva er verdien av Noran etter at selskapet opptar gjeld?
Markedsverdien av selskapet = V = EK + G = 100.000.000 + 100.000.000 = 200.000.000
Oppgave 3
(OBS: Dette har vi ikke gått gjennom i forelesning enda – iallfall ikke på campus Trondheim.)
Callamare ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 28 millioner kroner årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 14 %, risikofri rente er 3 %, og forventet risikopremie er 6 %. Callamare opptar nå gjeld for 100 millioner kroner til markedsrente på 5 %. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad (gjeld/egenkapital) regnet til markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og at selskapet betaler 27% selskapsskatt. (Se bort fra investor-skatt, sE=sK=0).
a) Hva blir egenkapitalkostnaden etter refinansieringen?
Dette er et relativt greit uttrykk. Egenkapitalkostnaden er en funksjon av kapitalkostnaden for gjeld (Kg), kapitalkostnaden for et selskap finansiert med 100% egenkapital (Ku), bedriftsskatten (Sb) og gjeldsgraden (G/E):
Ke = Ku + (Ku – Kg)*G/E*(1-Sb)
Med våre tall:
Ke = 0,14 + (0,14-0,05)*1*(1-0,27) = 0,2057 = 20,57%
b) Hva blir totalkapitalkostnad av refinansieringen?
Her må vi finne vektet gjennomsnitlig kaptialkostnad (WACC – Weighted Average Cost of Capital), og justere den for skatt. Det er ikke noe vanskeligere enn å bruke den formelen vi kjenner fra tidligere kurs, og justere for skatt.
Vi ganger kapitalkostnaden for egenkapital og gjeld med vektingen av henholdsvis egenkapital og gjeld (altså andelen. I vårt tilfelle 50% av hver)
Altså, generelt:
Kt = (Ke*We) + (Kg*Wg)*(1-Sb)
Med våre tall:
Kt = (0,2057*0,5)+(0,05*0,5)*(1-0,27) = 0,1211 =12,11%
c) Hva er verdien av Callamare når selskapet er 100% egenkapitalfinansiert?
Minner om at vi fortsatt forholder oss til Miller og Modiglianis forutsetninger.
Kontantstrømmen forutsettes evigvarende, og som evige annuiteter flest kan man beregne selskapsverdien ved å neddiskontere årlig forventet kontantstrøm med avkastningskravet for et gjeldfritt selskap (Ku). Vi må justere den årlige forventede kontantstrømmen (E(OFRS)) for skatt ved å legge til skatteleddet.
Altså, generelt:
Vu = (E(OFRS)*(1-Sb)) / Ku
Med våre tall:
Vu = (28.000.000*(1-0,27)) / 0,14 = 146.000.000
d) Hva er verdien av Callamare etter at selskapet opptar gjeld?
Den generelle formelen er:
Vm = Vu + PG*N*
Hvor:
–Vm er altså er verdien av selskapet når det er delvis gjeldsfinansiert
–Vu er verdien av et 100% egenkapitalfinansiert selskap
–PG er pålydende gjeld
–PG * N* (PG ganget med N* – altså Nstjerne. Litt forvirrende ettersom jeg bruker stjerne som gangetegn også). PG*Nstjerne er verdien av renteskattfordelen ved gjeld.
N* defineres som:
[1-(1-Sb)*(1-Se)] / (1-Sk)
Som vi ser i oppgaveteksten at vi har ettleddsbeskatning, altså skal vi se bort fra investorskatt, hvilket betyr at Se og Sk = 0. Da ser vi at uttrykket blir:
1 – (1-Sb) * (1-0) / (1-0) —> = 1- (1-Sb) / 1 —–> = Sb
Da kan vi se at formelen Vm = Vu + PG*N* blir:
Vm = Vu + PG*Sb
Med våre tall:
146.000.000 + 100.000.000*0,27 = 173.000.000
Det innføres nå investor-skatt, sE=sK=27%.
e) Hva er nå verdien av Callamare etter at selskapet opptar gjeld?
Nå har vi fått investorskatt. Investorskatten er imidlertid lik selskapsskatten, så den som har gransket uttrykket for N* vil se at dette ikke vil gjøre mye forskjell på verdien av selskapet. Vi skal likevel regne det på vanlig måte. Kanskje lærer vi noe 😀
Formelen blir fremdeles lik den i oppgave d)
Vm = Vu + PG*N* – bare at nå er i utgangspunktet ikke N* lengre lik Sb, men vi må regne ut uttrykke, slik at vi får:
Vm = Vu + PG*[1-(1-Sb)*(1-Se) / (1-Sk)
Med våre tall:
Vm = 146.000.000 + 100.000.000*[1 – ((1-0,27)*(1-0,27)) / (1-0,27)]
Vm = 146.000.000 + 100.000.000*0,27 = 173.000.000
Som du kanskje ser ble N* lik Sb likevel, ettersom investorskatt og selskapsskatt i oppgaven er like.
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
Oppgave 4
Cansas ASA har en gjeldsgrad på 0,5. Selskapets investeringsbeta er 1,1, mens aksjebetaen er 1,5. Risikofri rente er 4%, og forventet avkastning på markedsporteføljen er 10%. Se bort fra skatt.
a) Hva er den systematiske risiko for selskapets gjeld?
Denne formelen husker vi fra tidligere kurs:
βi = βe*We + βg*Wg
Med våre tall:
1,1 = 1,5*2/3 + βg*1/3
1,1 = 1 + 0,33βg
0,1 = 0,33βg
βg = 0,3
b) Hva er kapitalkostnaden til gjelden?
Uttrykket for kapitalkostnaden til gjelden er:
Kg = rf+βg * [E(Rm) – rf * S*)
hvor
– rf er risikofri lånerente
– βg systematisk risiko for gjelden
– E(Rm) er forventet markedsavkastning
– S* er skattefaktoren. Den uttrykkes som (1-Sk)/(1-Se) hvor Sk og Se er henholdvis skatt på renteinntekt og egenkapitalinntekt.
Med våre tall:
0,04+0,3*[0,10-0,04]=0,058 = 5,8%
c) Hva betyr det at gjelden har en beta-verdi som er større enn null? Bruk maks. 3 linjer på svaret.
Dersom gjelden har en betaverdi som er større enn null, betyr det at gjelden har risiko. Med en gjeldsbeta større enn null finnes det konkursrisiko. Dersom det er sjanse for konkurs, vil en del av investeringsrisikoen bli veltet over fra eierne til kreditorene. For å gå litt utover de tre linjene, vil dette føre til at effektiv lånerente må stige over risikofri rente for å kompensere for den investeringsrisikoen som kreditorene må bære.
Oppgave 5
Tre-års spotrente er i dag 4%, og fire-års spotrente er 5%.
a) Hva er terminrenten fra år tre til år fire, (3f4)?
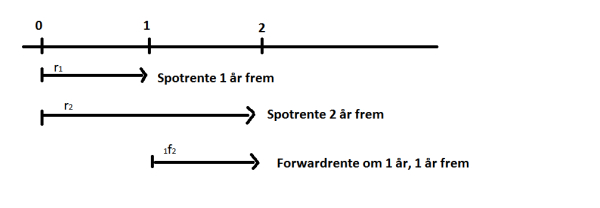
Implisitte terminrenter bygger på obeserverte effektive nullkupong-statsobligasjonsrenter.
Under forventningshypotensen (samt likviditetspremieteorien og markedssegmenteringsteorien, men disse er ikke viet plass i dette kurset) vil 1f2 som vist på paint-tegningen over være et anslag på en ettårsrente neste år. Det vil med andre ord være r1 om ett år.
Den generelle formelen bygger på et geometrisk gjennomsnitt:
Dette uttrykket kan generaliseres, og det er litt lettere å huske til eksamen:
I vårt tilfelle, blir det slik (jeg tar hele utredningen, men legg merke til at vi kommer frem til det generelle uttrykket som står over til slutt):
Med våre tall:
[(1+0,005)^4 / (1+0,04)^3] – 1 = 0,0805 = 8,05%
b) Gi en kort beskrivelse av forventningsteorien. Bruk maks 5 linjer på svaret.
Jeg bruker litt mer enn 5 linjer.
Forventningsteorien bygger kort fortalt på at teminstrukturkurven formes etter investorenes tanker om fremtidens rentenivå. Terminstrukturen vil være stigende dersom man forventer at rentenivået i markedet vil øke, og motsatt dersom man forventer at den vil falle. Dersom du ser for deg at en investor har valget mellom å kjøpe en obligasjon med enten lang eller kort løpetid, og den effektive renten er den samme på de to verdipapirene. Da er det lett å forstå at investoren ikke ville kjøpt obligasjonen med lang løpetid dersom han eller hun forventer at renten skal øke. Da ville investoren kjøpt en obligasjon med kort løpetid, og heller reinvestert pengene ved forfall. Dersom renten imidlertid forventes å falle, ville investoren kjøpt den lange obligasjonen – ja faktisk kunne investoren vært interessert i å kjøpe en lang obligasjon med lavere effektiv rente enn den korte også, avhengig av hvor stort rentefall investoren forventer.
Vi antar at kapitalmarkedskonkurransen er så sterk at de implisitte terminrentene i dagens lange rente blir lik de forventede fremtidige ettårsrentene i markedet. Forventningsteorien sier altså at du skal kunne oppnå samme avkastning ved å kjøpe en 2-åring (obligasjon med 2 års løpetid) som ved å kjøpe en ettåring i dag, og en ny ettåring om ett år. Altså at en toåring skal ha samme verdi som to påfølgende ettåringer. Det betyr også at en 4-åring skal gi samme avkastning som om du kjøper en 3-åring i dag, og en ettåring om 3 år.
Oppgave 6
Atona ASA er 100 % egenkapitalfinansiert. Selskapet har 1 million utestående aksjer med en markedsverdi på $100 per aksje. Atona trenger $40 millioner til et nytt prosjekt og bestemmer seg for å hente ny egenkapital i markedet. Selskapet gjør en emisjon med forkjøpsrett for gamle aksjonærer. Emisjonskursen blir satt til $80 per aksje. Se bort fra skatt.
1. Hva er en emisjon?
En emisjon er en finansieringsform som selskaper benytter når de har behov for mer egenkapital. Dette gjøres ved at selskapet mot innskudd i penger utsteder nye aksjer til dem som allerede eier aksjer i selskapet og/eller til noen som ikke eier aksjer i selskapet fra før.
2. Hva er en tegningsrett?
En tegningsrett gir deg rett (men ikke plikt) til å tegne og få tildelt nye aksjer i en emisjon i selskapet til en bestemt i pris, og i et bestemt tidsrom (tegningsperioden). Tegningsretten har normalt en økonomisk verdi dersom tegningskursen er lavere enn aksjekursen i markedet. Tegningsretter som ikke benyttes eller selges er uten verdi. De bortfaller etter tegningsperioden uten kompensasjon til eierne. Med andre ord bør du selge tegningsretten din dersom du ikke tenker å bruke den, hvis ikke er det et rent tap for deg, da aksjekursen kommer til å synke, uten at du blir kompensert med fortjeneste ved salg av tegningsretten (eventuelt fortjeneste i form av rabatt på aksjen hvis du velger å tegne deg)
Et eksempel:
(http://e24.no/boers-og-finans/bw-offshore-limited/bw-offshore-henter-penger-langt-under-dagens-kurs/23723858)
I sommerferien fikk jeg beskjed om en fortrinnsrettsemisjon i selskapet jeg har aksjer i; BW Offshore Limited, en av verdens ledende tilbydere innen utleie og drift av enheter for offshore, flytende produksjon og lagring. Selskapet er notert på Oslo Børs. Som mange har fått med seg er kanskje ikke offshore stedet hvor man ønsker å ha alle sparepengene sine plassert for tiden, men man trenger da litt spenning i hverdagen. Det er enorme restruktureringer innen olje og offshore for tiden. Styret i BWO hadde, som en del av en overordnet refinansiering av selskapet, vedtatt å gjennomføre en garantert fortrinnsrettet emisjon på inntil 856 millioner kroner, ved å utstede hele 8.599.810.000 nye aksjer til en tegningskurs på 0,10 øre per nye aksje.
Som aksjonær i BWO ble jeg tildelt tegningsretter. Disse tegningsrettene ga meg rett til å tegne meg for aksjer i fortrinnsrettsemisjonen. Jeg fikk tildelt ca 12,49 tegningsretter for hver aksje jeg hadde i selskapet. Hver tegningsrett ga meg rett til å kjøpe én ny aksje. Med andre ord fikk jeg mulighet til å kjøpe 12,49 nye aksjer til 0,10 kroner for hver aksje jeg hadde. Jeg kunne tegnet meg for flere enn det, men jeg hadde ikke vært garantert å fått dem. Dette ville avhenge av hvor mange som eventuelt ikke benyttet seg av sine tegningsretter.
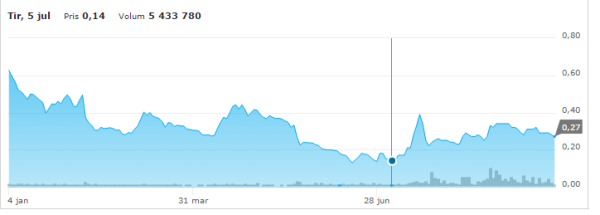
Tegningsrettene poppet opp i nettbanken i nettbanken min hos Nordnet, som jeg bruker til å handle verdipapirer. Da hadde jeg valget om enten å bruke tegningsrettene til å tegne meg for nye aksjer, eller selge dem på samme måte som jeg ville solgt en “vanlig aksje”. Disse tegningsrettene ble omsatt for omtrent 5 øre. Det betyr at hvis jeg hadde tegnet meg hadde min kostnad pr aksje (hvis vi ser bort fra kurtasje) vært 15 øre pr aksje (10 øre i emisjonskurs og 5 øre i alternativkostnad ved ikke å selge dem). Aksjekursen i dag er på 27 øre, så det var mulighet for noe kortsiktig gevinst på akkurat disse aksjene. Uten at jeg skal spekulere i kursbevegelsene: den justerte aksjekursen i starten av tegningsperioden var på så lite som 0,14 øre, som kanskje kan forklare hvorfor noen valgte å selge sine tegningsretter?
Sånn i utgangspunktet så denne emisjonen veldig attraktiv ut for meg som aksjonær. Hva jeg valgte å gjøre med tegningsrettene får være en hemmelighet.
La oss ta en titt på oppgavene.
a) Hva blir ex-rights-kursen?
De trenger 40.000.000 til det nye prosjektet, og setter emisjonskursen til 80. Da må de utstede: 40.000.000/80=500.000 nye aksjer
Ex-rights-kursen er altså den kursen aksjen forventes å få i markedet etter at emisjonen er gjennomført. Formelen for den teoretiske ex-rights-kursen er:
Px = [(n*P0) + (m*Pe)] / (n+m)
hvor:
–n er antall gamle aksjer
–m er antall nye aksjer
–P0 er kursen før emisjonen (rights-on)
–Pe er emisjonskursen
Med våre tall:
(1.000.0000*100) + (500.000*80) / (1.000.0000 + 500.000)
= 93,33
b) Hva er verdien av en tegningsrett?
Verdien av tegningsretten:
Tn = (Px-Pe)*1/N
hvor
–Px er ex-rights-kursen
–N = n/m, altså gamle aksjer delt på nye aksjer.
Med våre tall:
N = n/m = 1.000.000/500.000 = 2
(93,33-80)* 1/2
=6,67
c) Anna Berg eier 20 aksjer i Atona før emisjonen, hvor mange tegningsretter får hun tildelt?
Dette spørsmålet har ikke et entydig svar. I pensumboka står det at “antall tegningsretter tilsvarer antall utestående aksjer. En investor med 50 aksjer i et selskap får derfor 50 tegningsretter ved enhver nyemisjon i selskapet”. Dette er jo åpenbart ikke helt riktig i et hvert tilfelle, jfr det jeg skrev om emisjonen i BW Offshore, hvor jeg fikk utstedt 12,49 tegningsretter per aksje jeg hadde. Dette ville imidlertid ha tilsvart at jeg hadde fått én tegningsrett per aksje, og at hver tegningsrett hadde gitt meg muligheten til å kjøpe 12,49 aksjer. Jeg har sendt en mail til foreleseren min for å få klarhet i dette, og svar hvorfor boka og foilene i kurset er så bastant. Det viktigste er at tegningsrettene du får gir deg mulighet til å opprettholde din relative (prosentvise) eierandel i selskapet.
Med andre ord, skal vi følge fagansvarlig sin tilnærming, vil Anna Berg få 20 tegningsretter. Ettersom forholdet mellom gamle og nye aksjer = 500.000/1.000.000 = 0,5 får hun bare kjøpt en halv aksje pr. tegningsrett. Hun får altså kjøpt 10 nye aksjer med sine 20 tegningsretter.
Alternativt, dersom selskapet ville utstede tegningsretter som ga et tegningsforhold 1:1 hadde selskapet måtte gitt Anna 20*0,5 = 10 tegningsretter, da forholdet mellom gamle og nye aksjer er 0,5 nye aksjer pr gamle.
d) Hvilket beløp må Anna Berg investere hvis hun deltar i emisjonen og benytter alle sine tegningsretter?
Anna kan kjøpe 10 nye aksjer. Emisjonskursen er 80 dollar per aksje. Altså må hun investere 800 dollar.
e) Hvor stor andel av Atona eier Anna Berg etter emisjonen?
Eierandelen er:
20+10 / 1.000.000 + 500.000 = 30/1.500.000 = 0.00002
Anna eier 0,002% av Atona.
Det er ikke en del av oppgaven, men:
Hva var eierandelen hennes før emisjonen?
20/1.000.000 = 0.00002 = 0,002%. Ergo, hun har gjennom å benytte seg av tegningsrettene sine opprettholdt sin eierandel etter emisjonen.
Håper dere lærte noe. Rop ut hvis dere finner noe feil, eller ønsker å diskutere det som står skrevet.