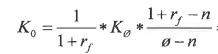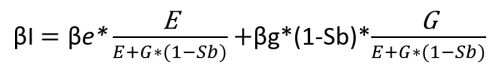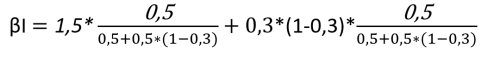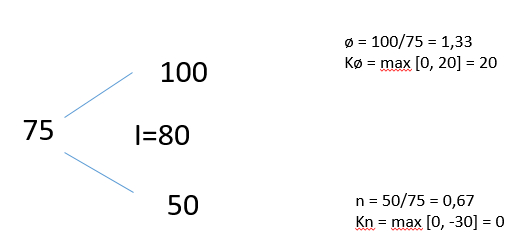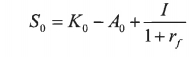Finansiell styring

Posted on 01.12.201619.04.2022

Finansiell styring – Eksamen H2013

Hei alle sammen. Dette blir det siste flervalgssettet jeg løser på bloggen i dette faget. Tenker at vi har gått gjennom det meste nå. Kanskje jeg løser noen sett som er mer lik den vi skal få på mandag. Dere vil kanskje legge merke til at jeg ikke er like omstendelig på oppgavene i dette innlegget, og det er fordi jeg har løst de før i de andre innleggene. Anbefaler dere å sjekke de andre innleggene hvis dere ikke skjønner hvor tallene kommer fra, før dere spør i kommentarfeltet 🙂

OBS: Når jeg prater om “univers A, B, C” osv, refererer jeg til de ulike universene av skatt/gjeld. Du bør lese dette korte innlegget før du setter i gang:
Gjeldsfinansiering og verdi

Tid for vårrengjøring? Knalltilbud på robotstøvsugere med mopp

1. Retro ASA antar at overskudd før renter og skatt neste år vil avhenge av etterspørselen etter varene i deres nye produktserie. På bakgrunn av en pilotundersøkelse har de kommet frem til følgende prognose for overskudd før renter og skatt neste år og i all overskuelig fremtid:

Tilstand	Sannsynlighet	OFRS
God	0,5	10 mill
Veldig god	0,4	15 mill
Ekstremt god	0,1	30 mill

Retro har 1 million utestående aksjer med en markedsverdi på 100 kroner per aksje, og 100 millioner kroner i lån til 5 % rente. Lånet er evigvarende. Se bort fra skatt.
Hva er Retros forventede overskudd per aksje neste år?
(a) 9,00 kroner
(b) 13,33 kroner
(c) 14,00 kroner
(d) 18,33 kroner

E(OFRS) = 10*0,5+15*0,4+30*0,1 = 14 mill
Rente: 100*0,05 = 5
E(OPA) = 14-5 = 9 kroner
2. Retro ASA antar at overskudd før renter og skatt neste år vil avhenge av etterspørselen etter varene i deres nye produktserie. På bakgrunn av en pilotundersøkelse har de kommet frem til følgende prognose for overskudd før renter og skatt neste år og i all overskuelig fremtid:

Tilstand	Sannsynlighet	OFRS
God	0,5	10 mill
Veldig god	0,4	15 mill
Ekstremt god	0,1	30 mill

Retro har 1 million utestående aksjer med en markedsverdi på 100 kroner per aksje, og 100 millioner kroner i lån til 5 % rente. Lånet er evigvarende. Se bort fra skatt.
Hva er Retros egenkapitalkostnad?
(a) 4,5 %
(b) 7,0 %
(c) 9,0 %
(d) 14,0 %

Uten skatt: Selskapets verdi = E(OFRS) / Kt
Selskapets verdi = EK + Gjeld = 100 + 100 = 200 mill
200 = 14 /Kt
Kt = 14/200
Kt = 0,07

Ke = Kt + (Kt – Kg)*G/EK
Ke = 0,07 + (0,07-0,05)*1
Ke = 0,09 = 9%

3. Retro ASA antar at overskudd før renter og skatt neste år vil avhenge av etterspørselen etter varene i deres nye produktserie. På bakgrunn av en pilotundersøkelse har de kommet frem til følgende prognose for overskudd før renter og skatt neste år og i all overskuelig fremtid:

Tilstand	Sannsynlighet	OFRS
God	0,5	10 mill
Veldig god	0,4	15 mill
Ekstremt god	0,1	30 mill

Retro har 1 million utestående aksjer med en markedsverdi på 100 kroner per aksje, og 100 millioner kroner i lån til 5 % rente. Lånet er evigvarende. Se bort fra skatt.
Hva er Retros totalkapitalkostnad?
(a) 4,5 %
(b) 7,0 %
(c) 9,0 %
(d) 14,0 %

Utregnet i forrige oppgave:
Uten skatt: Selskapets verdi = E(OFRS) / Kt
Selskapets verdi = EK + Gjeld = 100 + 100 = 200 mill
200 = 14 /Kt
Kt = 14/200
Kt = 0,07 = 7%

4. Apollo ASA er 100 % egenkapitalfinansiert. Overskuddet før renter og skatt blir enten 30 millioner kroner eller 50 millioner kroner årlig i overskuelig fremtid. Det er samme sannsynlighet for de to utfallene. Apollos egenkapitalbeta er 1,2, forventet avkastning på markedsporteføljen er 10 % og risikofri rente er 3 %. Se bort fra skatt.
Hva er verdien av Apollo?
(a) 40 millioner kroner
(b) 263 millioner kroner
(c) 351 millioner kroner
(d) 400 millioner kroner

E(OFRS) = 40 mill
Kt = 0,03 + (0,10-0,03)*1,2
Kt = 11,4%

V = 40/0,114 = 351 mill

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

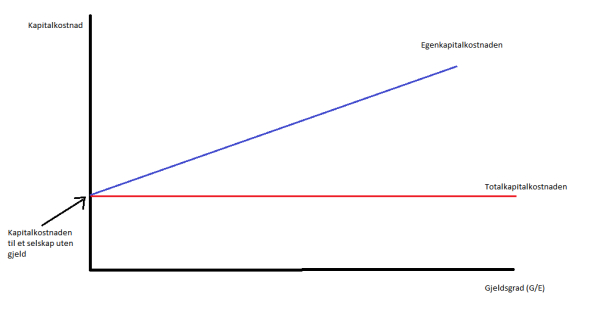
5. Et 100% egenkapitalfinansiert selskap har en egenkapitalkostnad på 10 %. Selskapet endrer kapitalstruktur til gjeldsgrad lik 1 (gjeld/egenkapital=1). Lånerenten er 5 %. Forutsett perfekte kapitalmarkeder og ingen skatter.
Hvorfor er egenkapitalkostnaden høyere når gjeldsgraden er 1 enn den er når gjeldsgraden er null?
(a) Fordi verdien av selskapet øker når selskapet tar opp lån.
(b) Fordi verdien av selskapet reduseres når selskapet tar opp lån.
(c) Fordi risikoen i egenkapitalen reduseres når selskapet tar opp lån.
(d) Fordi risikoen i egenkapitalen øker når selskapet tar opp lån.

Økt gjeldsgrad betyr mer gjeld. Mer gjeld betyr flere finansielle forpliktelser. Risikoen for eierne øker (std.avviket til OPA). Dette kan du lese mer om i kapittel 6 i boka.

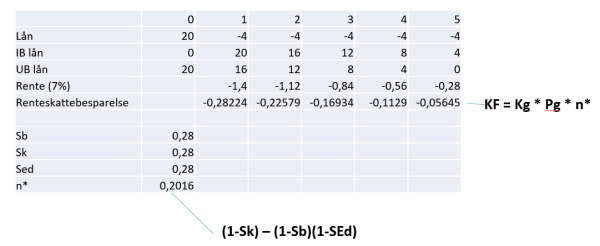
6. Lagune ASA har nettopp fått en ny 3-års kontrakt. Denne 3-års kontrakten krever en investering på 120 millioner kroner. Lagune forventer å finansiere prosjektet med egenkapital og et 3-årig serielån. Lagune betaler 4 % rente på lånet og lånet tilbakebetales med like avdrag hvert år. Målsatt gjeldsandel er 50 %. Selskapet forventer en kontantstrøm på 50 millioner kroner etter skatt i hvert av de tre årene. Prosjektets investeringsbeta er anslått til 1,2, markedets risikopremie er 7 %, og risikofri rente er 4 %. Selskapet betaler 28 % skatt. Anta at Modigliani & Millers ettleddsbeskatning (M&M63) gjelder (sK=sE=0). Lagune beregner gjeldsandel og gjeldskapasitet ut fra bokførte verdier.
Hva vil nåverdien av investeringen være dersom selskapet hadde vært 100% egenkapitalfinansiert?
(a) -1,260 millioner kroner
(b) -0,729 millioner kroner
(c) 1,260 millioner kroner
(d) 10,263 millioner kroner

E(Ri) = 0,04 + 0,07*1,2 = 12,4%

NPV = -120 + 50/1,124 + 50/1,124^2 + 50/1,124^3 = -0,729

7. Lagune ASA har nettopp fått en ny 3-års kontrakt. Denne 3-års-kontrakten krever en investering på 120 millioner kroner. Lagune forventer å finansiere prosjektet med egenkapital og et 3-årig serielån. Lagune betaler 4 % rente på lånet og lånet tilbakebetales med like avdrag hvert år. Målsatt gjeldsandel er 50 %. Selskapet forventer en kontantstrøm på 50 millioner kroner etter skatt i hvert av de tre årene. Prosjektets investeringsbeta er anslått til 1,2, markedets risikopremie er 7 %, og risikofri rente er 4 %. Selskapet betaler 28 % skatt. Anta at Modigliani & Millers ettleddsbeskatning (M&M63) gjelder (sK=sE=0). Lagune beregner gjeldsandel og gjeldskapasitet ut fra bokførte verdier.
Hva er nåverdien av renteskattegevinsten?
(a) -2,360 millioner kroner
(b) -0,729 millioner kroner
(c) 1,260 millioner kroner
(d) 10,263 millioner kroner

Sett opp et oppsett likt de jeg har satt opp i de tidligere innleggene. Du finner f.eks. at i år 1 er renten 2,4. Da er RSG = 2,4*0,28 = 0,672. Legg inn kontantstrømmen i kalkulatoren med diskonteringsrente 4% (lånerenten)

NV av RSG = 0,672/1,04 + 0,448/1,04^2 + 0,224/1,04^3 = 1,25949
8. Lagune ASA har nettopp fått en ny 3-års kontrakt. Denne 3-års kontrakten krever en investering på 120 millioner kroner. Lagune forventer å finansiere prosjektet med egenkapital og et 3-årig serielån. Lagune betaler 4 % rente på lånet og lånet tilbakebetales med like avdrag hvert år. Målsatt gjeldsandel er 50 %. Selskapet forventer en kontantstrøm på 50 millioner kroner etter skatt i hvert av de tre årene. Prosjektets investeringsbeta er anslått til 1,2, markedets risikopremie er 7 %, og risikofri rente er 4 %. Selskapet betaler 28 % skatt. Anta at Modigliani & Millers ettleddsbeskatning (M&M63) gjelder (sK=sE=0). Lagune beregner gjeldsandel og gjeldskapasitet ut fra bokførte verdier.
Hva er selskapets justerte nåverdi?
(a) -2,360 millioner kroner
(b) -0,729 millioner kroner
(c) 0,531 millioner kroner
(d) 1,260 millioner kroner

JNV = NV(invest) + NV(finans)
JNV = -0,729 + 1,25949 = 0,5304

9. Selskapet Extan AS ønsker å investere i ny bedrift som skal produsere elektriske sykler. Extan trenger 40 millioner kroner til denne investering som forventes å ha en levetid på 3 år. Selskapets målsatte gjeldsandel er 60 %. Extan kan låne til 6 % rente. Innovasjon Norge tilbyr Extan et subsidiert serielån til 2 % fordi elektriske sykler kan redusere bilbruken og dermed CO2 utslippet. Lånet som skal nedbetales med like store avdrag hvert år, er det eneste lånet Extan har. Se bort fra skatt.
Hva er nåverdien av det subsidierte lånet?
(a) 1,74 millioner kroner
(b) 3,78 millioner kroner
(c) 4,00 millioner kroner
(d) 6,00 millioner kroner

Sett opp en kontantstrøm med:
Lånopptak/avdrag
rente
CF

Regn ut NV av CF til lånet med neddiskonteringsrente 6%

+24 – 8,48/1,06 osv..
NPV = 1,74

10. Natron ASA har 8 millioner utestående aksjer. Selskapet antar at overskuddet før renter og skatt neste år vil bli 110 millioner kroner. Selskapet har 40 millioner kroner i gjeld. Gjelden er et banklån til 5 % rente. Natron vil utbetale 60 % av forventet overskudd per aksje i dividende. Det er ingen skatter.
Hva er forventet endring i Natrons aksjekurs på ex-dividende dagen? Forutsett at det bare er dividendeutbetalingen som endrer aksjens verdi.
(a) -13,75 kroner
(b) – 8,10 kroner
(c) 8,10 kroner
(d) 13,75 kroner

E(OFRS) = 110
E(OER) = 110 – (40*0,05) = 108
E(OPA) = 108/8 = 13,5
Utbytte = 13,5*0,6 = 8,1

Aksjekursen vil teoretisk sett endres tilsvarende aksjeutbytte pr aksje. Endring: -8,1

11. Du kjøper 100 aksjer for 80 000 kroner 1. januar i 2012. 1. juni 2012 mottar du 11 kroner i dividende per aksje. 1. desember 2012 selger du aksjene for 80 000 kroner. Både dividende og kursgevinst beskattes likt, med 28 % ved utbetaling.
Hva er månedlig avkastning etter skatt på denne investeringen?
(a) 0,09 %
(b) 0,13%
(c) 1,06 %
(d) 1,26 %

Legg inn i finanskalkulator:
-80.000 i januar,
0 i feb, mars, april og mai.
1100*(1-0,28) =792 i juni. | fordi du må skatte av utbyttet
0 i juli, august, sept, okt, nov.
I desember legger du inn: 80.000 (ingen gevinst, derfor ingen skatt)

IRR = 0,09%

12. Ask AS holder konstant kapasitet og forventer evig årlig overskudd før renter og skatt på 60 millioner kroner. Skattesatsen er 20 % på selskapsnivå, og selskapet betaler full dividende. Selskapet har ingen gjeld, og kapitalkostnaden er 8,0 % etter skatt.
Ask ønsker å endre kapitalstruktur og tar opp et lån på 150 millioner kroner til 3 % rente før skatt. Kreditorskatten er 20 % og dividendeskatten er 20 %.
Hva er Ask verd nå?
(a) 600 millioner kroner
(b) 630 millioner kroner
(c) 720 millioner kroner
(d) 750 millioner kroner

Verdi uten gjeld (Vu) = 60 (1-0,20) / 0,08 = 600
Verdi med gjeld = Vu + PG*N*

N* = n*/(1-Sk)
n* = (1-Sk) – (1-Sb)*(1-SEd) = 0,8 – 0,8*0,8 = 0,16
N* = 0,16/0,8 = 0,2

Verdi med gjeld = 600 + 150*0,2 = 630 mill

13. Irrelevans-resultatet sier at det ikke går an å påvirke verdien av et selskap gjennom dividendebeslutningen. Det betyr at netto verdieffekt er lik null uansett hva dividenden settes til.
Hvilken av de følgende forutsetninger gjelder for irrelevans-resultatet?
(a) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
(b) Egenkapitalbeskatningen er nøytral.
(c) Alt annet enn dividendepolitikken holdes konstant.
(d) Både (a),(b) og (c).

Se tidligere innlegg

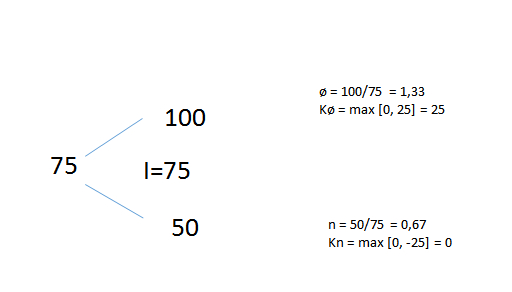
14. Aksjer i selskapet Polli ASA koster i dag 100 kroner. Om tre måneder vil kursen enten være 110 kroner eller 90 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 100 kroner og tre måneder til forfall. Risikofri årsrente er 4 %.
Hva er kjøpsopsjonens verdi i dag?
(a) 4,46 kroner
(b) 5,45 kroner
(c) 6,73 kroner
(d) 7,03 kroner

A0: 100
I: 100
ø: 1,10
n: 0,9
Kø: 10
Kn: 0
Rf: 0,01

K0 = (1/1,01) * 10 * (1,01-0,9) / (1,10-0,9)
K0 = 5,4455

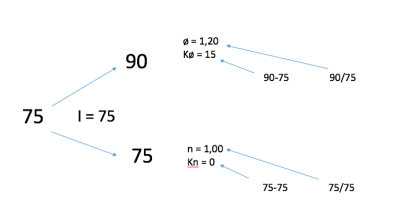
15. Aksjer i selskapet Polli ASA koster i dag 100 kroner. Om tre måneder vil kursen enten være 110 kroner eller 90 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 100 kroner og tre måneder til forfall. Risikofri årsrente er 4 %.
Hva er salgsopsjonens verdi i dag?
(a) 4,46 kroner
(b) 5,45 kroner
(c) 6,73 kroner
(d) 7,03 kroner

K0 – S0 = A0 – I/1+Rf
S0 = K0 – A0 + I/Rf
S0 = 5,4455 – 100 + 100/1,01
S0 = 4,455

16. Hvordan kan du ved hjelp av en aksje, en kjøpsopsjon og en salgsopsjon oppnå en risikofri investering? Anta at kjøpsopsjonen og salgsopsjonen har samme innløsningskurs og tid til forfall.
(a) Kjøp en aksje, selg en kjøpsopsjon, og lån nåverdien av innløsningskursen.
(b) Kjøp en aksje, kjøp en kjøpsopsjon, og selg en salgsopsjon.
(c) Kjøp en aksje, selg en kjøpsopsjon, og selg en salgsopsjon.
(d) Verken (a), b), eller (c).

A + S = B + K

A = aksje
S = salgsopsjon
B = obligasjon (risikofri komponent)
K = kjøpsopsjon

B = A + S – K
Kjøp aksje, Kjøp salgsopsjon, selg kjøpsopsjon

17. En obligasjon pålydende 1000 kroner og 9 år til forfall koster i dag 1100 kroner. Kupongrenten er 7 % og den utbetales årlig.
Hva er markedsrenten for denne obligasjonen i dag?
(a) 5,00 %
(b) 5,56 %
(c) 7,00 %
(d) 7,81 %

Legg inn kontantstrøm med: minus 1100 i år 0, og deretter 70 i hvert år frem til og med år 8. I år 9 legger du inn 1070.
IRR = 5,5579

18. Laks ASA har bestemt seg for å øke aksjekapitalen med 2 mill. kroner ved en emisjon med fortrinnsrett. Emisjonskursen er fastsatt til 100 kroner per aksje. Laks har 100.000 aksjer utestående med en markedspris på 118 kroner per aksje.
Hva er den teoretiske verdien av en tegningsrett?
(a) 0,6 kroner
(b) 3,0 kroner
(c) 15,0 kroner
(d) 18,0 kroner

I dette innlegget kan du lese mer om emisjoner, fortrinnsrett og tegningsretter: http://hobbyokonomen.blogg.no/1473846237_14092016.html

Verdien av tegningsretten:
Tn = (Px-Pe)*1/N
hvor
–Px er ex-rights-kursen
–N = n/m, altså gamle aksjer delt på nye aksjer.

De skal hente inn 2.000.000 ved å utstede nye aksjer til 100 kroner. Ergo må de utstede 20.000 nye aksjer.

Ex-rights-kursen er altså den kursen aksjen forventes å få i markedet etter at emisjonen er gjennomført. Formelen for den teoretiske ex-rights-kursen er:

Px = [(n*P0) + (m*Pe)] / (n+m)
hvor:
–n er antall gamle aksjer
–m er antall nye aksjer
–P0 er kursen før emisjonen (rights-on)
–Pe er emisjonskursen

Px = ((100.000*118) + (20.000*100)) / 120.000
Px = 115

Tn = (Px-Pe)*1/N
Tn = 115-100*1/ (100.000/20.000)
Tn = 15*0,2
Tn = 3

19. Anta at Modigliani-Miller forutsetningene i en verden uten skatter holder. Superwidget ASA er i dag 100% egenkapitalfinansiert med en beta på 1,5. Forventet avkastning på markedsporteføøljen er 10% og risikofre rente er 5%.
Superwidget planlegger nå å erstatte en firedel (¼) av egenkapitalen med risikofri gjeld.
Hva er forventet egenkapitalavkastning i Superwidget etter endringen i kapitalstrukturen?
(a) 5,0%
(b) 10,0%
(c) 12,5%
(d) 15,0%

Finner Ke uten gjeld:
Ke = Kt = Rf + (E(Rm) – Rf)*Beta
Ke = Kt = 0,05 + 0,05*1,5
Ke = Kt = 12,5%

Med gjeld:
Ke = Kt + (Kt-Kg)*G/E
Ke = 0,125 + (0,125-0,05)*1/3
Ke = 15%

20. Perpetuum AS er i øyeblikket helt ut egenkapitalfinansiert. Selskapet har 10.000 aksjer utestående. Årlig dividende har vært og forventes også i fremtiden å være fast med kr 12 per aksje. Dividende er nettopp utbetalt. Egenkapitalbeta i selskapet er 1,2. Markedets risikopremie er 5%, og risikofri rente er 6%. Selskapets skattesats er 20%.
Perpetuum planlegger nå å låne 200.000 kroner for å bruke pengene til å kjøpe tilbake noen av de utestående aksjene. Lånet vil være evigvarende og risikofritt.
Hva er verdien av Perpetuums egenkapital etter endringen I kapitalstrukturen?
(a) kr 640.000
(b) kr 800.000
(c) kr 840.000
(d) kr 1.000.000

Vi bør finne aksjekursen først:

Kt = Ke = 0,06 + 0,05*1,2
Kt = Ke = 0,12

P0 = D1/Ke
P0 = 12/0,12 = 100 kroner pr aksje
Selskapets verdi uten gjeld er 100*100.000 = 1 mill

Verdi med gjeld = Verdi uten gjeld + PG*N* | ettersom det er ettleddsskatt er N* = Sb, dette har jeg utledet i et tidligere innlegg.
Verdi med gjeld = 1 mill + 200.000*0,2 = 1.040.000

Enterprise Value = EK + G
EK = Enterprise Value – G
EK = 1.040.000 – 200.000 = 840.000

21. Anta at Modigliani-Miller forutsetningene i en verden uten skatter holder. Gulf ASA har utestående 100.000 aksjer med en kurs på kr 50 per aksje, Forventet egenkapitalavkastning er 10%. Selskapet har også 2 mill. kroner i gjeld med en rente lik markedsrenten på 5%.
Hva er forventet egenkapitalavkastning dersom Gulf bestemmer seg for å endre kapitalstrukturen til 100% egenkapital?
(a) 5,00%
(b) 8,57%
(c) 10,00%
(d) 12,00%

Beta:
EK: 100.000*50 = 5.000.000
Ke(med) = Ke(uten) + (Ke(uten) – Kg)*G/EK
0,10 = X + (X – 0,05)*2/5
0,10 = X + 0,4X – 0,02
1,4X = 0,12
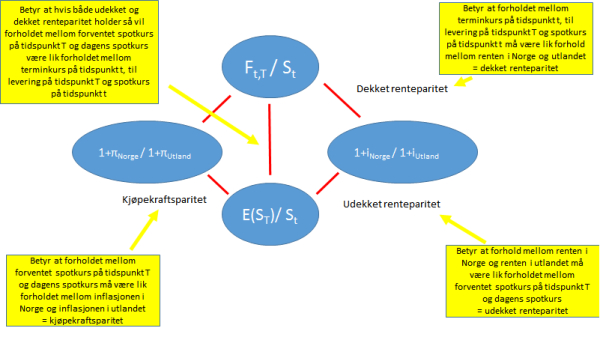
X = Ke = 8,57%
22. Dagens spotkurs mellom Euro og norsk krone er 1 EUR = 7,890 NOK, mens 1-års termin kurs er 1 EUR = 7,900 NOK. I Eurosonen er årsrenten 3% og årlig inflasjonsrate 2%. Anta at både dekket og udekket renteparitet holder.
Hva er forventet årlig inflasjon i Norge?
(a) 0,98%
(b) 2,13%
(c) 3,13%
(d) 9,80%

Denne oppgaven ble trukket fra eksamen i 2013 pga logiske brister i oppbyggingen og feil i fasit. Ikke bruk tid på den.
23. Dagens spotkurs mellom amerikanske dollar og norsk krone er 1 USD = 6,105 NOK. Anta at du kjøper 100 Widget aksjer til en pris på $50 per stykk, og at du selger aksjene om ett år til $52 per aksje. Widget utbetaler ikke dividend dette året. Kursen om ett år er 1 USD = 6,040 NOK.
Hvilken avkastning målt i norske kroner har du hatt på denne aksjeinvesteringen?
(a) 2,89%
(b) 4,00%
(c) 5,12%
(d) 6,15%

År 0: – (50*6,105*100) = -30.525
År 1: (52*6,040*100) = 31,408
IRR: 2,89%

24. I dag er Happy ASA finansiert med 60% gjeld og 40 % egenkapital (markedsverdier). Markedsverdien av gjeld er 200 mill. kroner med en rente på 5%. Selskapets skattesats er 30%, mens både kursgevinst og utbytte beskattes med 15%. Skatt på renteinntekt er 35%. Konkursrisikoen er lik null.
Hva ville verdien av Happy vært dersom de i stedet hadde valgt å finansiere utelukkende med egenkapital?
(a) 316 mill. kroner
(b) 324 mill. kroner
(c) 333 mill. kroner
(d) 347 mill. kroner

Vm = Vu + PG*N*
N* = n*/1-Sk
n* = (1-Sk) – (1-Sb)*(1-SEd)
n* = 0,65 – 0,7*0,85 = 0,055
N* = 0,055 / 0,65 = 0,0846

Verdien av gjelda er 200 millioner, og den utgjør 60% av Vm —> 200 mill/0,6 = 333,333 mill

Vm = Vu + PG*N*
333,33 = Vu + 200*0,0846
Vu = 333,33 – 16,92
Vu = 316,41 mill

25. Aksjekursen i HarryJet er kr 100. I morgen er eks-dividende dag for en dividende på kr 12 per aksje. Dividendeskattesatsen er 10%, mens skattesats for kursgevinst er 28%.
Hvilken eks-dividende kurs på aksjen vil gjøre deg indifferent mellom å selge aksjen i dag eller i morgen (eks-dividende dagen)?
(a) kr 100,00
(b) kr 88,00
(c) kr 85,00
(d) kr 82,50

P0 = 100
SEd = 10%
SEg = 28%

Selge på tidspunkt 0: 100*0,72 = 72
Dividende på tidsp. 1: 12*0,9 = 10,8

Finn ut hvilken kurs du må selge på i morgen for å få samme gevinst som å selge i dag:
10,8 + X*0,72 = 72
X = 85

26. Neo ASA har 2 millioner aksjer utestående til en kurs på kr 80. Selskapet planlegger å emittere 1 million nye aksjer gjennom en emisjon med tegningsrett. Emisjonskursen er kr 60.
Hva er forventet ex-rights kurs?
(a) 67,33 kroner
(b) 73,33 kroner
(c) 80,00 kroner
(d) 83,67 kroner

Neo ASA planelegger å hente inn 1.000.000*60 = 60 millioner kroner
Ex-rights-kursen er altså den kursen aksjen forventes å få i markedet etter at emisjonen er gjennomført. Formelen for den teoretiske ex-rights-kursen er:

Px = [(n*P0) + (m*Pe)] / (n+m)
hvor:
–n er antall gamle aksjer
–m er antall nye aksjer
–P0 er kursen før emisjonen (rights-on)
–Pe er emisjonskursen

Px = (2.000.000*80) + (1.000.000*60) / (3.000.000)
Px = (160.000.000 + 60.000.000) / 3.000.000
Px = 73,33 kroner

27. Hvilket av følgende utsagn er korrekt?
(a) Verdien av en salgsopsjon øker med risikofri rente.
(b) Verdien av en kjøpsopsjon avtar med risikofri rente
(c) Verdien av en salgsopsjon avtar med innløsningskursen.
(d) Verdien av en kjøpsopsjon øker med tid til forfall.

Forklart i tidligere innlegg.

28. Vesla AS transporterer biler mellom Japan og Europa. Selskapet har nylig vurdert et prosjekt i en helt ny bransje. Investeringen vil være på 10 mill. kroner, og Vesla har estimert at prosjektet vil generere et overskudd før renter og skatt (OFRS) på 10 mill. kroner i all fremtid. Årlige avskrivninger (i all fremtid) vil være på 2 mill. kroner.
Det er to konkurrenter i bransjen. Begge konkurrentene er for tiden 100% egenkapitalfinansiert. Deres gjennomsnittlige beta er 0,7. Risikofri rente er 5%, markedets risikopremie er 6%, og selskapsskattesatsen er 30%.
Hva er verdien av dette prosjektet for et 100% egenkapitalfinansiert selskap?
(a) 87,8 mill. kroner
(b) 73,3 mill. kroner
(c) 66,1 mill. kroner
(d) 59,7 mill. |kroner

Kt = Ke = 0,05 + 0,06*0,7 = 9,2%

E(OFRS) = 10
Skatt = 10*0,3 = 3
Avskrivninger = 2

Innbetalt overskudd: 9 mill

Nåverdien av denne evige kontantstrømmen er: 9 / 0,092 = 97,82
Netto nåverdi = -10 + 97,82 = 87,82

29. Referer på nytt til informasjonen i oppgave 28. Anta nå at Vesla AS ønsker å finansiere prosjektet med en gjeldsgrad (gjeld/egenkapital) på 1. Anta videre at gjelden er risikofri.
Hva er veiet gjennomsnittlig kapitalkostnad?
(a) 6,4%
(b) 7,8%
(c) 8,6%
(d) 9,2%

Finner beta først:
βe = βt + (βt – βg)(1-Sb)*G/E
βe = 0,7 + (0,7- 0)(0,7)*1
βe = 1,19

Ke = Rf + (E(Rm – Rf) *βe
Ke = 0,05 + 0,06* 1,19
Ke = 0,1214

WACC (Kt) = We*Ke + Wg*Kg*(1-Sb)
WACC = 0,5*0,1214 + 0,5*0,05*0,7 = 7,82%

30. Et selskap har som mål å utbetale 60% av overskuddet som dividend. Selskapet ønsker imidlertid ikke at store variasjoner i overskuddet skal føre til tilsvarende store variasjoner i dividende, og velger derfor å justere som beskrevet i den såkalte Lintner-modellen med en justeringsfaktor på 40%. Fjorårets dividende var kr 20 per aksje. Årets forventede overskudd per aksje er kr 60.
Hva er forventet dividende per aksje i år?
(a) kr 17,30
(b) kr 20,00
(c) kr 26,40
(d) kr 30,00
Jeg har skrevet ganske mye om Lintner-modellen og hva den brukes til i dette innlegget: http://hobbyokonomen.blogg.no/1478084546_finansiell_styring__i.html
Formelen vi bruker er:
DPAt = DPA(t-1) + a*[(b*OPAt)-DPA(t-1)
hvor:
DPA = Dividende pr aksje
OPA = Overskudd pr aksje
a = justeringsfaktor
b = målsatt utbetalingsforhold

Formelen forteller oss at årets dividendeutbetaling = fjorårets utbetaling +/- noe. Justeringsleddet avhenger av hvor mye målsatt dividendeutbetaling (basert på utbetalingsforholdet og det faktiske overskuddet) avviker fra fjorårets utbetaling og hvor raskt bedriften ønsker at dividenden skal endres (hvor mye mer stabil dividenden skal være i forhold til overskuddet).

Med våre tall: DPAt = 20 +0,4*[(0,6*60)-20] = 26,4

Posted on 30.11.201619.04.2022

Finansiell styring – Eksamen V2013

OBS: Når jeg prater om “univers A, B, C” osv, refererer jeg til de ulike universene av skatt/gjeld. Du bør lese dette korte innlegget før du setter i gang:
Gjeldsfinansiering og verdi

1. I en binomisk opsjonsmodell er kjøpsopsjonens verdi avhengig av:
(a) Dagens pris på den underliggende aksjen.
(b) Sannsynligheten for at den underliggende aksjen stiger eller synker.
(c) Volatiliteten til den underliggende aksjen.
(d) Både (a) og (c).

Dette påvirker kjøpsopsjonens verdi
– Prisen på det underliggende instrumentet (aksjen)
– Volatilitet (svingninger, standardavvik) i aksjekursen øker verdien av opsjonen, fordi den gir mindre risiko enn en aksje som svinger mye.
– Tid til forfall. Jo lengre tid det er til forfall, jo større er sjansen for at opsjonen ved forfall er lønnsom å benytte seg av (“in the money”). Det gir også mening at en rett (uten plikt) er mer verdt jo lengre du har retten.
– Innløsningskurs. Verdien av kjøpsopsjoner avtar med økende innløsningskurs, fordi jo høyere innløsningskursen er, jo mindre er sannsynligheten for at aksjekursen ved forfall er høyere enn innløsningskursen.
– Risikofri rente. Jo høyere rente, jo lavere nåverdi av innløsningskursen.

2. Hvordan kan du ved hjelp av en aksje, en kjøpsopsjon og en salgsopsjon oppnå en risikofri investering?
(a) Kjøp en aksje, selg en kjøpsopsjon, og kjøp en salgsopsjon.
(b) Kjøp en aksje, kjøp en kjøpsopsjon, og selg en salgsopsjon.
(c) Kjøp en aksje, selg en kjøpsopsjon, og selg en salgsopsjon.
(d) Selg en aksje, kjøp en kjøpsopsjon, og kjøp en salgsopsjon.

Bruker følgende sammenheng:
A + S = B + K
Hvor:
A = aksje
S = salgsopsjon
B = obligasjon (risikofri komponent)
K = kjøpsopsjon

B = A + S – K

3. Anta at skattesystemet favoriserer gjeld, det vil si at det ikke er nøytralisert av rentenivået, og at gjelden er risikofri uansett gjeldsgrad.
Hvilken av følgende påstander er korrekt dersom selskapet øker sin gjeldsgrad utover dagens nivå?
(a) Egenkapitalkostnaden øker og totalkapitalkostnaden synker.
(b) Gjeldskostnaden og totalkapitalkostnaden er begge konstante.
(c) Totalkapitalkostnaden stiger.
(d) Verdien av selskapet synker.

-Dersom skattesystemet er nøytralt vil Kt være uavhengig av gjeldsgrad
-Dersom skattesystemet favoriserer EK vil Kt være stigende med økt gjeldsgrad
-Dersom skattesystemet favoriserer gjeld vil Kt være synkende med økt gjeldsgrad
-Vi har flere ganger konkludert med at Ke er stigende med økt gjeldsgrad.

4. Hvilken eller hvilke av disse forutsetningene gjelder for dividende-irrelevansresultatet?
(a) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
(b) Egenkapitalbeskatningen er nøytral.
(c) Alt annet enn dividendepoltikken holdes konstant.
(d) Både (a), (b), og (c).

Irrelevansprinsippet sier at under gitte forutsetninger vil det ikke være mulig å påvirke verdien av et selskap gjennom dividendepolitikk. Den påstår at det er et nullsumspill som gjør at effekten av dividendeendring vil nøytraliseres av en tilsvarende endring i aksjekurs. Forutsetningene er:
1) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
2) Egenkapitalbeskatningen er nøytral.
3) Alt annet enn dividendepolitikken holdes konstant (dividendepolitikken påvirker inne investerings- og gjeldsgradsbeslutninger).

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

5. Et selskap har nylig utstedt en 10-års obligasjon med 6% kupongrente. Markedsrenten på tilsvarende obligasjoner er 4% i dag.
Obligasjonen omsettes i dag:
(a) Til pålydende.
(b) Over pålydende.
(c) Under pålydende
(d) Det er ikke nok informasjon til å besvare spørsmålet.

Kupongrente > markedets avkastningskrav –> pris > pålydende
Kupongrente < markedets avkastningskrav –> pris < pålydende
Kupongrente = markedets avkastningskrav –> pris = pålydende

6. Prisen på en aksje i Olives ASA dagen før retten til dividende bortfaller (siste rights-on dag) er $60. Dividenden er på $8 per aksje. Investorer betaler 28% skatt på kapitalgevinst og dividendeinntekt.
Hva er forventet pris på en aksje første ex-rights dag?
(a) $ 5,76
(b) $ 8,00
(c) $43,20
(d) $52,00

Aksjekursen vil synke tilsvarende dividende pr aksje, altså 8 dollar.

7. Markedsverdien på aksjene i Ruccula ASA er 100 kroner pr. aksje den 01.01.2012. Ruccula er 100% egenkapitalfinansiert. Selskapets aksjonærer har et avkastningskrav på 18% etter skatt. Ruccula betaler 28% selskapsskatt. Selskapet utbetaler ikke dividende i løpet av året.
Hva er forventet aksjekurs 31.12.2012?
(a) 85 kroner
(b) 113 kroner
(c) 118 kroner
(d) 151 kroner

Aksjonærenes avkastningskrav er 18% etter skatt. Aksjekursen blir 100*1,18 = 118 kroner.

8. Aksjekapitalen i Morningside ASA består av 4 millioner aksjer verdsatt til 50 kroner pr. aksje den 01.01.2012. Forventet overskudd neste år er 24 millioner kroner etter skatt. Morningside er 100% egenkapitalfinansiert. Selskapets aksjonærer har et avkastningskrav på 14% etter skatt. Morningside betaler 28% selskapsskatt. Selskapet utbetaler 60% av overskuddet etter selskapsskatt i dividende på årets siste dag.
Hva er forventet aksjekurs 31.12.2012 like etter dividendeutbetalingen?
(a) 44,00 kroner
(b) 46,40 kroner
(c) 53,40 kroner
(d) 56,00 kroner

Ettersom vi får oppgitt avkastningskravet etter skatt:
50*1,14 – (24mill*0,6)/4mill = 57 – 3,6 = 53,40 kroner

9. Aksjer i selskapet Nikki ASA koster i dag 80 kroner. Om tre måneder vil kursen enten være 100 kroner eller 80 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 85 kroner og tre måneder til forfall. Risikofri årsrente er 4%.
Hva er salgsopsjonens verdi i dag?
(a) 0,59 kroner
(b) 4,75 kroner
(c) 5,00 kroner
(d) 5,25 kroner

Regn ut dette på samme måte som i de andre innleggene.
ø = 1,25
n = 1,00
Kø = 15
Kn = 0
Husk: årsrente = 4% –> kvartalsrente =1%
Jeg kom frem til at K0 = 0,594

Tar videre utgangspunkt i salg-kjøp paritet
K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf

S0 = 0,594 – 80 + 85/1,01 = 4,75 kroner

10. Aksjer i selskapet Pepper ASA koster i dag 40 kroner. Om tre måneder vil kursen enten være 30 kroner eller 50 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 45 kroner og forfall om tre måneder. Aksjer i selskapet Salt ASA koster i dag 40 kroner. Om tre måneder vil kursen enten være 10 kroner eller 70 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 45 kroner og forfall om tre måneder. Risikofri årsrente er 4%.
Hvilken av følgende uttalelser er korrekt?
(a) Prisen på kjøpsopsjonen i Pepper er lik prisen på kjøpsopsjonen i Salt.
(b) Prisen på kjøpsopsjonen i Pepper er høyere enn prisen på kjøpsopsjonen i Salt.
(c) Prisen på kjøpsopsjonen i Pepper er lavere enn prisen på kjøpsopsjonen i Salt.
(d) Prisen på kjøpsopsjonene er uavhengig av årsrenten.

Det er lett å se at standardavviket (risikoen) er større i Salt enn i Pepper. Verdien av en opsjon er stigende med økt risiko, så c) er riktig.

11. Markedsverdien av egenkapitalen i Nightlife ASA er 100 million NOK. Det er 5 million utestående aksjer. Kjøps- og salgs opsjoner på aksjene i Nightlife med tre måneder til forfall og en innløsningskurs på 24 NOK, koster i dag henholdsvis 4 NOK og 7,50 NOK.
Hva er tre-måneders risikofri rente?
(a) 2,1%
(b) 2,7%
(c) 4,2%
(d) 4,8%

A0 = 100/5 = 20

K0 – S0 = A0 – I/1+rf
I/1+rf = A0 – K0 + S0
24/1+rf = 20 – 4 + 7,5
24 = 23,5 + 23,5rf
0,5/23,5 = rf
rf = 0,021 = 2,1%

12. Vegaform ASA er 100% egenkapital finansiert. Selskapet har 1 million utestående aksjer med en markedsverdi på $100 per aksje. Vegaform bestemmer seg for å forandre kapitalstruktur. Selskapet låner $60 millioner til 5% rente og bruker lånet til tilbakekjøp av egne aksjer. Lånet er evigvarende. Selskapet betaler 30% selskapsskatt. (Se bort fra investor- og kreditorskatt).
Hva er totalverdien av Vegaform etter forandringen av kapitalstrukturen?
(a) $ 70 millioner
(b) $100 millioner
(c) $118 millioner
(d) $160 millioner

Selskapet tilbakekjøper aksjer for 60 millioner. Dette reduserer antallet utestående aksjer i markedet. I balansen føres tilbakekjøpte aksjer under egne aksjer i form av et negativt tall. Dette vil påvirke selskapsverdien, men ikke aksjeverdien. Hvorfor?

Se for deg at aksjeprisen i dette selskapet er 100 kroner og at det er 1 million utestående aksjer. Verdien til selskapet er da 100 millioner. Dersom selskapet tilbakekjøper aksjer for 10 millioner (altså 100.000 aksjer) vil verdien av egenkapitalen (selskapsverdien i et selskap uten gjeld) være 10 millioner mindre, altså 90 millioner.. Antall utestående aksjer vil være 100.000 færre, altså 900.000. Teoretisk aksjepris vil da være 90.000.000/900.000 = 100

Til oppgaven:
Tidligere var verdien på selskapet:
1.000.000*100 = 100.000.000 dollar.

Balansen påvirkes.
EK: 100.000.000 – tilbakekjøpte aksjer – gjeld
EK: 100.000.000 – 60.000.000 – 60.000.000
EK: -20.000.000
G: 60.000.000
Totalkapital: 60.000.000

Da finnes det flere måter å gjøre dette på. Vi kan f.eks. bruke denne sammenhengen
Verdi av bedrift med gjeld = verdi av bedrift uten gjeld + nåverdi av skattebesparelsen

Skattebesparelsen finner vi slik:
r*PG*Sb / Kg
0,05*60mill*0,30 / 0,05 = 18.000.000

Vm = Vu + NV(skattebesparelse)
Vm = 100.000.000 + 18.000.000 = 118.000.000

Alternativt:
V = 1.00.000*100 + 0,3*60.000.000 = 118.000.000

13. Anor ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 12 millioner kroner årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 11%, risikofri rente er 4%, og forventet risikopremie er 6%. Anor opptar nå gjeld for 60 millioner kroner til markedsrente på 6%. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad (gjeld/egenkapital) regnet til markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og se bort fra skatt.
Hvordan påvirkes selskapets egenkapitalkostnad av refinansieringen?
(a) Egenkapitalkostnaden blir uendret, 11%.
(b) Egenkapitalkostnaden øker fra 11% til 14%.
(c) Egenkapitalkostnaden øker fra 11% til 15%.
(d) Egenkapitalkostnaden øker fra 11% til 16%.

Ke før = Ku = 11%
[Ke = Ku + (Ku – Kg)*G/EK]
Ke = 0,11 + (0,11-0,06)*1
Ke = 16%

14. Selskapet Trolly ASA er finansiert med egenkapital og gjeld. Verdien av selskapet er gitt ved følgende formel: Vm = Vu + PG*N*⋅
hvor:
VM er verdien av selskapet med gjeld
VU er verdien av selskapet uten gjeld
PG er pålydende gjeld
N er skatteverdifaktoren
Hva er skatteverdifaktoren N under ett-leddsbeskatning?
(a) Den er lik selskapskatten.
(b) Den er lik investorskatten.
(c) Den er lik kreditorskatten.
(d) Den er alltid lik 28%.

N* = n*/(1-Sk)
n* = (1-Sk) – (1-Sb)*(1-SEd)

Dersom det er ettleddsskatt med f.eks Sb=28% er:
n* = (1-0) – (1-0,28)/(1-0)
n* = 1-0,72 / 1
n* = 0,28 = Sb

N* = 0,28/1 = 0,28 = Sb

15. Konsulentselskapet Astro AS har nettopp fått en ny 5-års kontrakt som forventes å gi følgende kontantstrøm etter skatt i de neste 5 årene, (tallene er i millioner kroner):

Tid	1	2	3	4	5
KS	100	110	150	170	180

Denne 5-årskontrakten (prosjektet) krever en investering på 500 millioner kroner. Astro forventer å finansiere prosjektet med egenkapital og et serielån. Astro betaler 5% rente på lånet. Målsatt gjeldandel er 50%. Prosjektets investeringsbeta er anslått til 1,0, markedets risikopremie er 6%, og risikofri rente er 4%. Selskapet betaler 28% skatt. Anta at Modigliani & Millers ett-leddsbeskatning (M&M63) gjelder (sK=sE=0).
Hva er nåverdien av prosjektet dersom det hadde vært 100% egenkapitalfinansiert?
(a) 22,39 millioner kroner
(b) 34,35 millioner kroner
(c) 38,90 millioner kroner
(d) 60,00 millioner kroner

Finner avkastningskravet:
E(Ri) = Rf + (E(Rm) – Rf)*Beta
E(Ri) = 0,04 + 0,6*1
E(Ri) = 10%

Legger inn kontantstrømmen oppgitt i oppgaven (med investeringsutgiften på -500 i år 0) i finanskalkulator med diskonteringsrente 10%
NPV = 22,39
16. Starlight ASA har nettopp akseptert en ny 5-års kontrakt. Denne 5-års kontrakten krever en investering på 400 millioner kroner. Starlight forventer å finansiere prosjektet med egenkapital og gjeld. Starlight betaler 5% renter på gjeld. Gjeldsandelen er 50% og gjelden er et 5-års lån som nedbetales med like avdrag ved utgangen av året. Prosjektets beta er anslått til 1.2, markedets risikopremie er 6% og risikofri rente er 4%. Selskapet betaler 28% skatt. Det er ingen investorskatt.
Hva er nåverdien av renteskattegevinsten? Starlight bruker bokbasert gjeldskapasitet.
(a) 7,51 MNOK
(b) 8,36 MNOK
(c) 8,88 MNOK
(d) 9,53 MNOK

Tid	0	1	2	3	4	5
KS	-200	100	150	170	200	200
IB lån	0	200	160	120	80	40
Avdrag		-40	-40	-40	-40	-40
UB lån	200	160	120	80	40	0
Rente (5%)		-10	-8	-6	-4	-2
Renteskattegevinst		2,8	2,24	1,68	1,12	0,56

Legg inn renteskattegevinsten på finanskalkulatoren med diskonteringsrente = lånerente = 0,05
NV = 7,51

17. Selskapet Kenz ASA planlegger å investere i et to-års prosjekt. Investeringen koster 20 millioner kroner, og forventes å gi en kontantstrøm etter skatt på 14 millioner kroner hvert av de to årene. Prosjektets investeringsbeta er anslått til 1,3, markedets risikopremie er 7%, og risikofri rente er 3%. Selskapet betaler 28% skatt. Investorer betaler ikke skatt (sK=sE=0). Prosjektet finansieres med 40% egenkapital og 60% gjeld. Gjelden er et lån til 5%, hele lånet tilbakebetales ved slutten av det andre året.
Hva er prosjektets justerte nåverdi?
(a) ? 3,63 millioner kroner
(b) 0,22 millioner kroner
(c) 3,63 millioner kroner
(d) 3,94 millioner kroner

	0	1	2
Investering/inntekter	-20	14	14
Lån	12		-12
IB lån	0	12	12
UB lån	12	12	0
Rente (5%)		0,6	0,6
Renteskattebesparelse (1)		0,168	0,168

Sb	0,28
Sk	0
Sed	0
n*	0,28

(1) Renteskattebesparelsen finner du ved: å multiplisere rentebeløpet med n*
n* = (1-Sk) – (1-Sb)*(1-Se)

18. Selskapet New Energy AS ønsker å investere i ny bedrift som skal produsere vindmøller. I første omgang trenger New Energy 12 millioner kroner til et pilot-prosjekt som forventes å ha en levetid på 3 år. Selskapets målsatte gjeldsandel er 60%. New Energy kan låne til 5% rente. I Klekk kommune er det stort behov for nye arbeidsplasser. Den lokale sparebanken tilbyr selskapet New Energy et subsidiert treårig serielån til 2% (billig lån) dersom den nye bedriften etablerer seg i Klekk kommune. Lånet skal nedbetales med like store avdrag hvert år. Se bort fra skatt.
Hva er nåverdien av det subsidierte lånet?
(a) 0,3985 millioner kroner
(b) 0,4252 millioner kroner
(c) 0,5320 millioner kroner
(d) 0,6655 millioner kroner

Her må du sette opp en kontantstrøm for lånet, og neddiskontere det med r=5%

	0	1	2	3
Opptak/avdrag	7,2
IB lån	0	7,2	4,8	2,4
Avdrag		-2,4	-2,4	-2,4
UB lån	7,2	4,8	2,4	0
Renter (2%)		-0,144	-0,096	-0,048
KS	7,2	-2,544	-2,496	-2,448

Jeg fikk NV = 0,3985 da jeg la det inn på kalkulatoren med diskoteringsrente 5%

19. Selskapene South ASA og North ASA er helt like bortsett fra at South er 100% egenkapital finansiert, mens North har en gjeldsgrad (gjeld/egenkaptial) på 1. Begge selskapene har markedsverdi på 20 millioner kroner. North har en gjeldskostnad på 4%. Forventet, evig overskudd før renter og skatt er 2 millioner kroner i begge selskapene. Se bort fra skatt.
Hva er totalkapitalkostnaden i de to selskapene?
(a) 10% i South og 10% i North.
(b) 10% i South og 14% i North.
(c) 10% i South og 16% i North.
(d) 14% i South og 16% i North.

Kt er uavhengig av finansieringen i et univers uten skatt. Alternativ a) er eneste alternativ hvor Kt i begge selskapene er lik. For ordens skyld:
[V = E(OFRS) / Kt]
Kt = E(OFRS) / V
Kt = 2/20
Kt = 0,10 = 10%

20. Selskapene South ASA og North ASA er helt like bortsett fra at South er 100% egenkapital-finansiert, mens North har en gjeldsgrad (gjeld/egenkapital) på 1. Begge selskapene har markedsverdi på 20 millioner kroner. North har en gjeldskostnad på 4%. Forventet, evig overskudd før renter og skatt er 2 millioner kroner i begge selskapene. Se bort fra skatt.
Hva er egenkapitalkostnaden i de to selskapene?
(a) 10% i South og 10% i North.
(b) 10% i South og 14% i North.
(c) 10% i South og 16% i North.
(d) 14% i South og 16% i North.

Egenkapitalkostnaden (Ke) er imidlertid avhengig av finansieringen. Den vil være økende med økt gjeldsgrad, med mindre gjelden er risikofri.
Ke i South vil være lik Kt, altså 10%

Ke i North kan vi regne ut på to måter:

Alternativ 1:
Ke = Kontantstrøm til eier / EK
Ke = 2.000.000 – (10.000.000*0,04) / 10.000.000
Ke = 1.600.000/10.000.000
Ke = 16%

Alternativ 2:
Ke = Ku + (Ku – Kg)*G/EK
Hvor Ku = totalkapitalkostnad uten gjeld
Ke = 0,10 + (0,10-0,04)*1
Ke = 16%

21. Amerikanske dollar noteres i Paris til 0,7293 og i Oslo til 5,8800. Euro noteres i Oslo til 7,72000.
Hvilken mulig arbitrasjegevinst kan du oppnå hvis du har 1 millioner kroner å investere?
(a) 12.398 kroner
(b) 13.546 kroner
(c) 44.369 kroner
(d) 70.000 kroner

Så:
Dollar:
Paris: EUR/USD = 0,7293
Oslo: NOK/USD = 5,8800
Euro:
Oslo: NOK/EUR = 7,72

Det gir oss krysskurs = EUR/USD * NOK/EUR = NOK/USD –> 0,7293*7,72 = 5,6301960
Vi ser at dollaren er “for dyr” i Norge. (5,5880 mot 5,6301960). Det betyr at vi kan oppnå gevinst ved å først veksle til Euro, så til USD, så tilbake til NOK.

1. Kjøper Euro i Norge for 1 million til kurs 7,72: 1.000.000/7,72 = 129.534 Euro.

2. Veksler disse EUR 129.534 til USD i Paris: 129.534/0,7293 = 177.614 Dollar.

3. Vi selger USD 177.614 i Norge: 177.614*5,88 = 1.044.370,32

Arbitrasjegevinst: 1.044.370,32 – 1.000.000 = 44.370,32

22. Dagskursen mellom enkelte valutaer er som følger:
1 EUR = 1,3300 USD, 1 EUR = 0,7050 GBP, 1 EUR = 0,9300 CHF.
Hva er dagskursen mellom amerikanske dollar og sveitsiske franc, samt mellom sveitsiske franc og britiske pund dersom det ikke foreligger noen arbitrasjemuligheter?
(a) 1 CHF = 1,2369 USD, 1 CHF = 0,6557 GBP
(b) 1 CHF = 0,6815 USD, 1 CHF = 1,3050 GBP
(c) 1 CHF = 0,8051 USD, 1 CHF = 1,5418 GBP
(d) 1 CHF = 1,4301 USD, 1 CHF = 0,7581 GBP

EUR/USD = 1,3300
EUR/GBP = 0,7050
EUR/CHF = 0,9300

EUR/CHF = 0,9300 betyr: CHF/EUR = 1/0,9300=1,0752688

Krysskurs: CHF/USD = CHF/EUR*EUR/USD
CHF/USD = 1,0752688*1,3300 = 1,4301

Krysskurs: CHF/GBP = CHF/EUR*EUR/GBP
CHF/GBP = 1,0752688*0,7050 = 0,7581

23. Den risikofrie årsrenten er 4% i USA og 2% i eurosonen. Dagskursen er 1 EUR = 1,30 USD.
Hva er 12 måneders terminkurs mellom EUR og USD dersom arbitrasjegevinster ikke er mulig?
(a) 1 EUR = 1,2750 USD
(b) 1 EUR = 1,3118 USD
(c) 1 EUR = 1,3255 USD
(d) 1 EUR = 1,4739 USD

[Terminkurs = Spot * (1+rente i hjemlandet) / (1+rente i utlandet)]
Terminkurs = 1,30* (1,04 / 1,02)
Terminkurs = 1,3255

24. Prisen for en kjøpsopsjon med 6 måneder til forfall er kr 12. Innløsningskursen er kr 75. Aksjeprisen på den underliggende aksjen er kr 80, og den risikofrie årsrenten er 5%.
Hva er prisen i likevekt på en tilsvarende salgsopsjon?
(a) kr 3,43
(b) kr 5,19
(c) kr 11,43
(d) kr 18,81

K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf
S0 = 12 – 80 + 75/1,025
S0 = 5,17

25. Et selskap som er 100% egenkapitalfinansiert er verdsatt til 100 mill. kroner. Selskapets skattesats er 30%.
Hva blir verdien av selskapet dersom det utsteder 50 mill. kroner i evigvarende gjeld og benytter pengene til å kjøpe tilbake aksjer?
(a) 65 mill. kroner
(b) 85 mill. kroner
(c) 100 mill. kroner
(d) 115 mill. kroner

Verdi med gjeld = 100 mill + (50mill*0,3) = 115 mill

26. Et 100% egenkapitalfinansiert selskap har en systematisk risiko målt ved beta på 1,2. Selskapet velger så å endre kapitalstrukturen til 50% egenkapital og 50% gjeld ved å ta opp et lån til 8% rente. Gjeldsbetaen er 0,2. Selskapet er ikke i skatteposisjon.
Hva blir selskapets egenkapitalbeta etter refinansieringen?
(a) 1,2
(b) 1,6
(c) 2,2
(d) 2,4

Ved 100% EK er βe og βt den samme. βe = βt =1,2
[βe = βt + (βt – βg)*G/EK]
– Betaen til totalkapitalen vil ikke ha forandret seg.
– Betaen til gjeld er 0, da gjelden er risikofri (jfr. oppgaveteksten)

βe = 1,2 + (1,2-0,2)*1
βe = 2,2

27. Modigliani og Millers hovedresultat 1 (M&M-1) i en verden uten skatt sier at:
(a) Markedsverdien av et selskap er uavhengig av selskapets kapitalstruktur.
(b) Markedsverdien av et selskaps gjeld er uavhengig av selskapets kapitalstruktur.
(c) Markedsverdien av et selskaps aksjekapital er uavhengig av selskapets kapitalstruktur.
(d) Markedsverdien av et selskaps aksjekapital er lik markedsverdien av selskapets gjeld.

Se innlegget: Gjeldsfinansiering og verdi

28. Selskap X har 100 aksjer utestående. Selskapets årlige resultat er 1.000 kroner som i sin helhet å utbetales som dividende. Denne dividenden forventer selskapet å utbetale i all overskuelig fremtid. Egenkapitalavkastningskravet er 10%.
Hva er forventet aksjekurs i dag?
(a) kr 9,90
(b) kr 90,00
(c) kr 100,00
(d) kr 110,00

V = 1.000 / 0,10 = 10.000
Aksjekurs = 10.000 / 100 = 100 kroner

29. En avgjørende forutsetning for dividendens irrelevans er at:
(a) Ingen usikkerhet om fremtidige aksjekurser.
(b) Det er ingen skatt på kursgevinst.
(c) Kapitalmarkedet er perfekt.
(d) Alle investeringer er risikofrie.

30. Et stort selskap mottar en lånegaranti fra staten. Med denne garantien er selskapet i stand til å låne 50 mill. kroner over fem år til 8% årsrente i sted for markedsrenten som er 10% per år.
Hvilken verdi har denne lånegarantien for selskapet? Se bort fra skatt.
(a) +53.79 mill. kroner
(b) +3.79 mill. kroner
(c) -3.79 mill. kroner
(d) -53.79 mill. kroner

	0	1	2	3	4	6
Opptak/avdrag	50
IB lån	0	50	50	50	50	50
Avdrag						-50
UB lån	50	50	50	50	50	0
Renter (8%)		-4	-4	-4	-4	-4
KS	50	-4	-4	-4	-4	-54

Regn ut nåverdien av kontantstrømmen med diskonteringsrente 10%
NV = 3,79 millioner kroner

Posted on 30.11.201619.04.2022

Finansiell styring – Eksamen H2012

Her er eksamen fra høsten 2012.

OBS: Når jeg prater om “univers A, B, C” osv, refererer jeg til de ulike universene av skatt/gjeld. Du bør lese dette korte innlegget før du setter i gang:
Gjeldsfinansiering og verdi

1. Markedsverdien på aksjene i Albacco ASA er 80 kroner pr. aksje den 01.01.2011. Albacco er
100 % egenkapitalfinansiert. Selskapets aksjonærer har et avkastningskrav på 15 % etter skatt.
Albacco betaler 20 % selskapsskatt. Selskapet utbetaler ikke dividende i løpet av året.
Hva er forventet aksjekurs 31.12.2011?
(a) 74 kroner.
(b) 90 kroner.
(c) 92 kroner.
(d) 110 kroner.

Eiernes kapital forventes økt med 15%: 80*1,15 = 92

2. Aksjekapitalen i Socco ASA består av 2 million aksjer verdsatt til 100 kroner pr. aksje den
01.01.2011. Forventet overskudd neste år er 18 millioner kroner etter skatt. Socco er 100 %
egenkapitalfinansiert. Selskapets aksjonærer har et avkastningskrav på 12 % etter skatt.
Socco betaler 20 % selskapsskatt. Selskapet utbetaler hele overskuddet etter selskapsskatt i
dividende på årets siste dag.
Hva er forventet aksjekurs 31.12.2011 like etter dividendeutbetalingen?
(a) 91 kroner
(b) 100 kroner
(c) 103 kroner
(d) 112 kroner

Ettersom vi får oppgitt avkastningskravet etter skatt:
100*1,12 – 18mill/2mill = 103

3. Aksjer i selskapet Telli ASA koster i dag 120 kroner. Om tre måneder vil kursen enten være
150 kroner eller 100 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med
innløsningskurs på 110 kroner og tre måned til forfall. Risikofri årsrente er 4 %.
Hva er salgsopsjonens verdi i dag?
(a) 4,86 kroner
(b) 5,72 kroner
(c) 16,81 kroner
(d) 19,09 kroner

Regn ut dette på samme måte som i de andre innleggene.
ø = 1,25
n = 0,83333
Kø = 40
Kn = 0
Husk: årsrente = 4% –> kvartalsrente =1%
Jeg kom frem til at K0 = 16,792

Tar videre utgangspunkt i salg-kjøp paritet
K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf

S0 = 16,792 – 120 + 110/1,01
S0 = 5,70

4. Aksjer i selskapet Focus ASA koster i dag 40 kroner. Om tre måneder vil kursen enten være
30 kroner eller 50 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med
innløsningskurs på 45 kroner. Aksjer i selskapet Consus ASA koster i dag 40 kroner. Om tre
måneder vil kursen enten være 10 kroner eller 70 kroner. Det omsettes salgs- og
kjøpsopsjoner på denne aksjen med innløsningskurs på 45 kroner og forfall om tre måned.
Risikofri årsrente er 4 %.
Hvilken av følgende uttalelser er korrekt?
(a) Prisen på kjøpsopsjonen i Focus er lik prisen på kjøpsopsjonen i Consus.
(b) Prisen på kjøpsopsjonen i Focus er høyere enn prisen på kjøpsopsjonen i Consus.
(c) Prisen på kjøpsopsjonen i Focus er lavere enn prisen på kjøpsopsjonen i Consus.
(d) Prisen på kjøpsopsjonene er uavhengig av årsrenten.

Det er lett å se at standardavviket (risikoen) er større i Consus enn i Focus. Verdien av en opsjon er stigende med økt risiko, så c) er riktig.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

5. Selskapet Talius ASA er finansiert med egenkapital og gjeld. Verdien av selskapet er gitt ved
følgende formel:
VM=VU+PG·N*
Hvor: VM er verdien av et selskap med gjeld
VU er verdien av et selskap uten gjeld
PG er pålydende gjeld
N* er skatteverdifaktoren
Hva viser skatteverdifaktoren N*?
(a) Skatteverdifaktoren viser nåverdien av prosjektets netto skattebesparelse.
(b) Skatteverdifaktoren viser nåverdien av netto skattebesparelse per gjeldskrone.
(c) Skatteverdifaktoren viser nåverdien av netto skattebesparelse i et selskap uten gjeld.
(d) Skatteverdifaktoren viser at et selskap med gjeld er mer verd enn et selskap uten gjeld.

Se: http://hobbyokonomen.blogg.no/1480082961_finansiell_styring__g.html

6. Kvantum ASA er 100 % egenkapital finansiert. Selskapet har 1 million utestående aksjer med
en markedsverdi på $100 per aksje. Kvantum bestemmer seg for å forandre kapitalstruktur.
Selskapet låner $60 millioner til 5 % rente og bruker lånet til tilbakekjøp av egne aksjer.
Lånet er evigvarende. Selskapet betaler 30 % selskapsskatt. (Se bort fra investor- og
kreditorskatt).
Hva er totalverdien av Kvantum etter forandringen av kapitalstrukturen?
(a) $ 70 millioner.
(b) $100 millioner.
(c) $118 millioner.
(d) $160 millioner.

Til oppgaven:
Tidligere var verdien på selskapet:
1.000.000*100 = 100.000.000 dollar.

Balansen påvirkes.
EK: 100.000.000 – tilbakekjøpte aksjer – gjeld
EK: 100.000.000 – 60.000.000 – 60.000.000
EK: -20.000.000
G: 60.000.000
Totalkapital: 60.000.000

Da finnes det flere måter å gjøre dette på. Vi kan f.eks. bruke denne sammenhengen
Verdi av bedrift med gjeld = verdi av bedrift uten gjeld + nåverdi av skattebesparelsen

Skattebesparelsen finner vi slik:
r*PG*Sb / Kg
0,05*60mill*0,30 / 0,05 = 18.000.000

Vm = Vu + NV(skattebesparelse)
Vm = 100.000.000 + 18.000.000 = 118.000.000

Alternativt:
V = 1.00.000*100 + 0,3*60.000.000 = 118.000.000

7. I en binomisk opsjonsmodell er kjøpsopsjonens verdi avhengig av:
(a) Dagens pris på den underliggende aksjen.
(b) Sannsynligheten for at den underliggende aksjen stiger eller synker.
(c) Volatiliteten til den underliggende aksjen.
(d) Både (a) og (c).

Dette påvirker opsjonens verdi:
– Dagens aksjekurs
– Volatilitet (svingninger, standardavvik) i aksjekursen øker verdien av opsjonen, fordi den gir mindre risiko enn en aksje som svinger mye.
– Tid til forfall. Jo lengre tid det er til forfall, jo større er sjansen for at opsjonen ved forfall er lønnsom å benytte seg av (“in the money”). Det gir også mening at en rett (uten plikt) er mer verdt jo lengre du har retten.
– Innløsningskurs. Verdien av kjøpsopsjoner avtar med økende innløsningskurs, fordi jo høyere innløsningskursen er, jo mindre er sannsynligheten for at aksjekursen ved forfall er høyere enn innløsningskursen.
– Risikofri rente. Jo høyere rente, jo lavere nåverdi av innløsningskursen.

8. Hvordan kan du ved hjelp av en aksje, en kjøpsopsjon og en salgsopsjon oppnå en risikofri
investering?
(a) Kjøp en aksje, selg en kjøpsopsjon, og kjøp en salgsopsjon.
(b) Kjøp en aksje, kjøp en kjøpsopsjon, og selg en salgsopsjon.
(c) Kjøp en aksje, selg en kjøpsopsjon, og selg en salgsopsjon.
(d) Selg en aksje, kjøp en kjøpsopsjon, og kjøp en salgsopsjon.

Bruker følgende sammenheng:
A + S = B + K
Hvor:
A = aksje
S = salgsopsjon
B = obligasjon (risikofri komponent)
K = kjøpsopsjon

B = A + S – K

9. Willy ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 12 millioner kroner
årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 11 %, risikofri rente er 4 %,
og forventet risikopremie er 6 %. Willy opptar nå gjeld for 60 millioner kroner til
markedsrente på 6 %. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad regnet til
markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og se bort fra skatt.
Hvordan påvirkes selskapets egenkapitalkostnad av refinansieringen?
(a) Egenkapitalkostnaden blir uendret, 11 %.
(b) Egenkapitalkostnaden øker fra 11 % til 14 %.
(c) Egenkapitalkostnaden øker fra 11 % til 15 %.
(d) Egenkapitalkostnaden øker fra 11 % til 16 %.

Ke før = Ku = 11%
[Ke = Ku + (Ku – Kg)*G/EK]
Ke = 0,11 + (0,11-0,06)*1
Ke = 16%
10. Anta at skattesystemet favoriserer gjeld, det vil si at det ikke er nøytralisert av rentenivået, og
at gjelden er risikofri uansett gjeldsgrad.
Hvilken av følgende påstander er korrekt dersom selskapet øker sin gjeldsgrad utover
dagens nivå?
(a) Egenkapitalkostnaden øker og totalkapitalkostnaden synker.
(b) Gjeldskostnaden og totalkapitalkostnaden er begge konstante.
(c) Totalkapitalkostnaden stiger.
(d) Verdien av selskapet synker.

11. Konsulentselskapet Petrogas ASA har nettopp fått en ny 5-års kontrakt som forventes å gi
følgende kontantstrøm etter skatt i de neste 5 årene, (tallene er i millioner kroner):

Tid	1	2	3	4	5
KS	100	150	170	200	200

Denne 5-års kontrakten krever en investering på 600 millioner kroner. Petrogas forventer å
finansiere prosjektet med egenkapital og et 5-årig serielån. Petrogas betaler 5 % rente på
lånet. Målsatt gjeldsandel er 50 %. Prosjektets investeringsbeta er anslått til 1,2, markedets
risikopremie er 6 %, og risikofri rente er 4 %. Selskapet betaler 28 % skatt. Anta at
Modigliani & Millers ett-leddsbeskatning (M&M63) gjelder (sK=sE=0).
Hva er nåverdien av prosjektet dersom det hadde vært 100 % egenkapitalfinansiert?
(a) – 20,28 millioner kroner
(b) – 16,71 millioner kroner
(c) 12,70 millioner kroner
(d) 18,32 millioner kroner

Finner avkastningskravet:
E(Ri) = Rf + (E(Rm) – Rf)*Beta
E(Ri) = 0,04 + 0,06*1,2
E(Ri) = 11,2%

Legger inn kontantstrømmen oppgitt i oppgaven (med investeringsutgiften på -600 i år 0) i finanskalkulator med diskonteringsrente 11,2%
NPV = -16,71

12. Konsulentselskapet Petrogas ASA har nettopp fått en ny 5-års kontrakt. Denne 5-års
kontrakten krever en investering på 600 millioner kroner. Petrogas forventer å finansiere
prosjektet med egenkapital og et 5-årig serielån. Petrogas betaler 5 % rente på lånet og lånet
tilbakebetales med like avdrag hvert år. Målsatt gjeldsandel er 50 %. Prosjektets
investeringsbeta er anslått til 1,2, markedets risikopremie er 6 %, og risikofri rente er 4 %.
Selskapet betaler 28 % skatt. Anta at Modigliani & Millers ett-leddsbeskatning (M&M63)
gjelder (sK=sE=0). Petrogas beregner gjeldsandel og gjeldskapasitet ut fra bokførte verdier.
Hva er nåverdien av renteskattegevinsten?
(a) 8,285 millioner kroner
(b) 10,975 millioner kroner
(c) 11,265 millioner kroner
(d) 14,895 millioner kroner

Tid	0	1	2	3	4	5
KS	-600	100	150	170	200	200
IB lån	0	300	240	180	120	60
Avdrag		-60	-60	-60	-60	-60
UB lån	300	240	180	120	60	0
Rente (5%)		-15	-12	-9	-6	-3
Renteskattegevinst		4,2	3,36	2,52	1,68	0,84

Legg inn renteskattegevinsten på finanskalkulatoren med diskonteringsrente = lånerente = 0,05
NV = 11,265

13. Selskapet Tilmo ASA planlegger å investere i et to-års prosjekt. Investeringen koster 20
millioner kroner, og forventes å gi en kontantstrøm etter skatt på 14 millioner kroner hvert av
de to årene. Prosjektets investeringsbeta er anslått til 1,3, markedets risikopremie er 7 %, og
risikofri rente er 3 %. Selskapet betaler 28 % skatt. Investorer betaler også 28 %
(sK=sE=28 %). Prosjektet finansieres med 40 % egenkapital og 60 % gjeld. Gjelden er et lån
til 5 %, hele lånet tilbakebetales ved slutten av det andre året.
Hva er prosjektets justerte nåverdi?
(a) – 3,63 millioner kroner
(b) 0,22 millioner kroner
(c) 3,63 millioner kroner
(d) 3,85 millioner kroner

Justert nåverdi = NV(investering) + NV(finansiering)

	0	1	2
Investering/inntekter	-20	14	14
Lån	12		-12
IB lån	0	12	12
UB lån	12	12	0
Rente (5%)		0,6	0,6
Renteskattebesparelse (1)		0,12096	0,12096

Sb	0,28
Sk	0,28
Sed	0,28
n*	0,2016

(1) Renteskattebesparelsen finner du ved: å multiplisere rentebeløpet med n*
n* = (1-Sk) – (1-Sb)*(1-Se)

Finner diskoteringsrenten:
E(Ri) = 0,03 + 0,07*1,3
E(Ri) = 12,1%

Nåverdien av investeringen finner du ved:
NV = -20 + 14/1,121 + 14/1,121^2
NV(investering) = 3,6296

Nåverdien av investeringen finner du ved (diskonteringsrente = rente etter skatt = 0,05*(1-0,28) = 3,6%:
NV = 0,12096/0,036 + 0,12096/0,036^2
NV(finansiering) = 0,229456

JNV = 3,6296 + 0,229456
JNV = 3,859 mill

14. Selskapet Sun AS ønsker å investere i ny bedrift som skal produsere solpanel. I første
omgang trenger Sun 12 millioner kroner til et prøveprosjekt som forventes å ha en levetid på
3 år. Selskapets målsatte gjeldsandel er 60 %. Sun kan låne til 5 % rente. I Holo kommune er
det stort behov for nye arbeidsplasser. Den lokale sparebanken tilbyr Sun et subsidiert
serielån til 2 % (billig lån) dersom den nye bedriften etablerer seg i Holo kommune. Lånet
skal nedbetales med like store avdrag hvert år. Se bort fra skatt.
Hva er nåverdien av det subsidierte lånet?
(a) 0,3985 millioner kroner
(b) 0,4252 millioner kroner
(c) 0,5320 millioner kroner
(d) 0,6655 millioner kroner

Her må du sette opp en kontantstrøm for lånet, og neddiskontere det med r=5%

	0	1	2	3
Opptak/avdrag	7,2
IB lån	0	7,2	4,8	2,4
Avdrag		-2,4	-2,4	-2,4
UB lån	7,2	4,8	2,4	0
Renter (2%)		-0,144	-0,096	-0,048
KS	7,2	-2,544	-2,496	-2,448

Jeg fikk NV = 0,3985 da jeg la det inn på kalkulatoren med diskoteringsrente 5%
15. Next ASA har 3 millioner utestående aksjer. Selskapet antar at overskuddet før renter og skatt neste år vil enten bli 24 millioner kroner eller 40 millioner kroner. Det er like stor sannsynlighet for de to utfallene. Selskapet har 40 millioner kroner i gjeld. Gjelden er et banklån til 5 % rente. Next vurderer å utbetale 60 % av det forventede overskuddet per aksje etter renter. Det er ingen skatter.
Hva er forventet endring i Nexts aksjekurs på ex-dividende dagen? (Forutsett at det bare er
dividendeutbetalingen som endrer aksjens verdi).
(a) -10,00 kroner
(b) – 6,00 kroner
(c) 6,00 kroner
(d) 10,00 kroner

E(OFRS) = 24 mill*0,5 + 40mill*0,5 = 32.000.000
E(OERS) = 32 mill – (40 mill * 0,05) = 30.000.000
E(OPA) = 10
Dividende: 60% = 6 kroner
Endring: -6 kroner

16. Balican ASA er et børsnotert selskap som opplever et plutselig og uventet etterspørselsjokk
for sine ferdigprodukter. Ledelsen anslår at dette har økt risikoen i kontantstrømmen fra
driften, men ikke forventningen. Uttrykt ved selskapets systematiske investeringsrisiko målt
ved beta, mener ledelsen at denne har steget fra 0,6 til 1,1.
Påvirkes verdiene til de eksisterende eierne av denne hendelsen?
(a) Eksisterende eieres verdier har økt.
(b) Eksisterende eieres verdier er uforandret.
(c) Eksisterende eieres verdier har sunket.
(d) Eksisterende eieres verdier er tapt.

Betaen har økt. Da øker også kapitalkostnaden, og nåverdien av selskapet går ned.

17. Aracas ASA er 100 % egenkapitalfinansiert. Overskuddet før renter og skatt blir enten 20
millioner kroner eller 50 millioner kroner årlig i overskuelig fremtid. Det er samme
sannsynlighet for de to utfallene. Aracas egenkapitalbeta er 1,8, forventet avkastning på
markedsporteføljen er 12 % og risikofri rente er 5 %. Se bort fra skatt.
Hva er verdien av Aracas?
(a) 114 millioner kroner
(b) 199 millioner kroner
(c) 284 millioner kroner
(d) 398 millioner kroner

Kt=Ke = 0,05 + (0,12-0,05)*1,8
Kt = Ke = 17,6%

E(OFRS) = 20 mill*0,50 + 50 mill*0,5 = 35.000.000

V = 35.000.000 / 0,176 = 199.000.000

18. Du kjøper en aksje i Petrus ASA for 60 kroner 1. januar i 2011. 1. juni 2011 mottar du 10
kroner i dividende. 1. desember 2011 selger du aksjen for 80 kroner. Både dividende og
kursgevinst beskattes likt, med 28 % ved utbetaling.
Hva er månedlig avkastning etter skatt på denne investeringen?
(a) 0,75 %
(b) 2,99 %
(c) 3,64 %
(d) 4,03 %

Legg inn i finanskalkulator:
-60 i januar,
0 i feb, mars, april og mai.
10*(1-0,28) =7,2 i juni. | fordi du må skatte av utbyttet
0 i juli, august, sept, okt, nov.
I desember legger du inn: 80 – (20*0,28) = 74,4 | fordi du må skatte av gevinsten på 20 kroner

IRR = 2,99%

19. Kanasus AS holder konstant kapasitet og forventer evig årlig overskudd før renter og
skatt på 40 millioner kroner. Skattesatsen er 20 % på selskapsnivå, og selskapet betaler
full dividende. Selskapet har ingen gjeld, og kapitalkostnaden er 8,0 % etter skatt.
Kanasus ønsker å endre kapitalstruktur og tar opp et lån på 150 millioner kroner til 3 %
rente før skatt. Kreditorskatten er 20 % og dividendeskatten er 20 %.
Hva er Kanasus verd dersom Millers likevektsmodell holder?
(a) 400 millioner kroner
(b) 424 millioner kroner
(c) 500 millioner kroner
(d) 550 millioner kroner

V = 40*0,8 / 0,08
V = 400

20. Irrelevans-resultatet sier at det ikke går an å påvirke verdien av et selskap gjennom
dividendebeslutningen. Det betyr at netto verdieffekt er lik null uansett hva dividenden
settes til.
Hvilken av de følgende forutsetninger gjelder for irrelevans-resultatet?
(a) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
(b) Egenkapitalbeskatningen er nøytral.
(c) Alt annet enn dividendepolitikken holdes konstant.
(d) Både (a),(b) og (c).

Bedriften må hele tiden ha en kontantstrømbalanse: Tilgang på penger = bruk av penger:
Kontantstrøm fra drift + ny gjeld + nytegnet egenkapital = renter + avdrag + nyinvestering + dividende

Med de forutsetningene jeg listet opp, betyr ligninga over at enhver endring i dividende vil kreve en tilsvarende endring i nytegnet egenkapital (emisjoner). Forutsetningene i irrelevansprinsippet sier at dersom vi øker dividendeutbetalingene med X kroner, vil det samtidig måtte utstedes nye aksjer for å hente inn X kroner. Når vi fordeler makredsverdien på flere aksjer, blir verdien på aksjen vannet ut, og mindre verdt.

Dette kan kanskje være litt komplisert forklart i boken, og kanskje ikke veldig intuitivt, men prøv å les litt om det i boka.

21. Hvilken av følgende uttalelser gjelder ikke for et selskaps gjeld?
(a) Tilbakebetaling er en forpliktelse for selskapet.
(b) Obligasjonseierne er deleiere i selskapet.
(c) Innebærer et skatteskjold for selskapet.
(d) Likvidering av selskapet kan skje hvis lånet ikke tilbakebetales i tide.

Når du kjøper en aksje blir du deleier av et selskap. Når du kjøper en obligasjon låner du ut penger til et selskap (kredittobligasjon). Du blir med andre ord ikke deleier. Du får ikke ta del i verdiskapningen i form av økt markedsverdi og dividende.

22. Anta en MM (Miller-Modigliani) verden med selskapsskatt og personlig inntektsskatt
(toleddsskatt). Ledelsen i et selskap er sikre på at man vil være i stand til å utnytte
gjeldsrenter til å redusere selskapets skattbare inntekt (dvs., det er ingen finansielle
krisekostnader). Selskapets inntektsskattesats er 30 %. Investorer betaler 40 % skatt på
mottatte renter, men ingen skatt på utbytte.
Ledelsen ønsker å øke selskapets gjeld med 2 millioner kroner og benytte dette til å kjøpe
tilbake selskapets egne aksjer i markedet.
Med hvor mye vil selskapets verdi endres ved dette?
(a) ─ 333.333 kroner
(b) ─ 285.714 kroner
(c) + 285.714 kroner
(d) + 333.333 kroner

n* = (1-Sk) – (1-Sb)*(1-SEd)
n* = (1-0,4) – (1-0,30)*(1-0) = -0,1

N* = n*/(1-Sk)
N* = -0,10 / 0,6 = -0,16667

Endring i verdi vil være: -0,16667*2.000.000 = -333.333 kroner
23. Forskjellen mellom et selskaps beta med og uten gjeld reflekterer:
(a) Selskapets forretningsrisiko.
(b) Selskapets finansielle risiko.
(c) Både forretningsrisiko og finansiell risiko for selskapet.
(d) Gjeldens skatteskjold (skattebesparelsen).

24. Hvilken av følgende uttalelser er korrekt?
(a) Kursen på en aksje pluss kursen på en kjøpsopsjon på aksjen tilsvarer prisen på en
salgsopsjon på aksjen med samme innløsningskurs pluss innløsningskursens nåverdi.
(b) Kursen på en aksje minus kursen på en salgsopsjon på aksjen tilsvarer kursen på en
kjøpsopsjon på aksjen med samme innløsningskurs minus innløsningskursens
nåverdi.
(c) Kursen på en aksje minus kursen på en salgsopsjon på aksjen tilsvarer kursen på en
kjøpsopsjon på aksjen med samme innløsningskurs minus innløsningskursens
nåverdi.
(d) Kursen på en aksje pluss kursen på en salgsopsjon på aksjen tilsvarer kursen på en
kjøpsopsjon på aksjen med samme innløsningskurs pluss innløsningskursens
nåverdi.

A + S = K + B

25. Hvilket av følgende utsagn om valutarisiko er feil?
(a) Valutastyring innebærer teknikker for å redusere og eliminere valutarisiko.
(b) Har du inntekter i utenlandsk valuta så kan du redusere valutarisikoen ved å ta opp
gjeld i samme valuta.
(c) Har du gjeld i utenlandsk valuta så kan du redusere valutarisikoen ved å kjøpe valuta
på termin (forward).
(d) Verken (a), (b) eller (c) er feil.

26. Hvilket av følgende utsagn om valutaforretninger og valutarisiko er korrekt?
(a) En terminforretning er en bindende avtale mellom banken og kunden om kjøp eller
salg av et bestemt valutabeløp til en på inngåelsesdagen fastsatt kurs, og med oppgjør
på et bestemt tidspunkt i fremtiden.
(b) Kunder med tilgodehavende i utenlandsk valuta som forfaller frem i tid, kan avdekke
(eliminere) valutarisikoen ved å selge valuta på termin (forward).
(c) Termintillegget/-fradraget (swapkursen) er en ren matematisk utregning basert på
spotkurs og rentesatser for de involverte valutaer.
(d) Både (a), (b) og (c) er korrekte.

27. Anta at du får oppgitt følgende krysskurser:
UTL/EUR 1,7023 (UTL = Utlandsk valuta)
UTL/NOK 6,5625 (EUR = euro)
(NOK = norske kroner)
Hva er krysskursen EUR/NOK?
(a) 0,2594
(b) 3,6343
(c) 3,8551
(d) 11,1713

Da blir:
EUR/NOK = 1/ (UTL/EUR) * UTL/NOK —> 1/1,7023*6,5625 = 3,8551

28. Hvilket av følgende utsagn om terminkursen (forward rate) i valutamarkedet er korrekt?
(a) Når renten på norske kroner er høyere enn renten på den utenlanske valuta vil det
alltid være et tillegg til spotkurs.
(b) Når renten på norske kroner er lavere enn renten på den utenlanske valuta vil det
alltid være et fradrag til spotkurs.
(c) I valutaterminologien kalles termintillegget/-fradraget også for swapkurs.
(d) Både (a), (b) og (c) er korrekte.

29. Du får oppgitt følgende spot og terminkurser for amerikanske dollar notert i Oslo:
Spot 5,5408
3 mnd. 5,6062
6 mnd. 5,6716
Dette innebærer at:
(a) Rentenivået i Norge er lavere enn i USA.
(b) Rentenivået i Norge er høyere enn i USA.
(c) Markedet forventer stigning i kursen på amerikanske dollar.
(d) Markedet forventer stigning i kursen på norske kroner.

[Terminkurs = Spot * (1+rente i hjemlandet) / (1+rente i utlandet)]
Terminkursene er større enn spotkursen. Det betyr at telleren må være større enn nevneren, og at renten i hjemlandet er større enn renten i utlandet.

30. Et selskap skal motta et sikkert beløp på 10 millioner Euro om 6 måneder. Selskapet har også
10 millioner i gjeld i Euro, men lånet er allerede valutasikret slik at man vet at man skal
betale 80 millioner kroner om 6 måneder. Dagens spotkurs for Euro er 7,60 og selskapet
forventer at denne vil være 7,80 om 6 måneder. Selskapets ledelse er urolig for at en endring
i valutakursen vil medføre at selskapet får en negativ kontantstrøm totalt sett i NOK. Man
ønsker derfor å benytte valutaopsjoner med innløsningskurs EUR 7,70 for å unngå dette.
For hvor stort Eurobeløp må selskapet kjøpe eller selge EUR opsjoner?
(a) Kjøp EUR kjøpsopsjon (“call”) for 10,39 millioner Euro
(b) Kjøp EUR salgsopsjon (“put”) for 10,39 millioner Euro
(c) Selg EUR kjøpsopsjon (“call”) for 10,39 millioner Euro
(d) Selg EUR salgsopsjon (“put”) for 10,39 millioner Euro

80 millioner / 7,7 = 10,3896.

Selskapet bør kjøpe salgsopsjoner (som gir dem rett til å selge) for 10,39 millioner Euro.

Posted on 26.11.201619.04.2022

Finansiell styring – Eksamen H2011

Her er løsningsforslag med utregninger og forklaringer på flervalgseksamen fra høst 2011. Når jeg refererer til “situasjon X” mener jeg situasjonene jeg har sammenfattet i dette innlegget: http://hobbyokonomen.blogg.no/1480082961_finansiell_styring__g.html
1. Albatros er 100% egenkapitalfinansiert. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalkostnaden er 12%. Se bort fra skatt.
Hva er Albatros? aksjebeta?
(a) 2,67
(b) 2,00
(c) 1,14
(d) 1,00

Bedriften er 100% finansiert av egenkapital, som betyr at egenkapitalkostnad og totalkapitalkostnad er det samme. Vi husker denne sammenhengen:
Totalkapitalkostnad = risikofri rente + risikopremie * beta
0,12 = 0,04 + 0,07*X
0,07X = 0,08
X = 1,14

2. Albatros er 100% egenkapitalfinansiert. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalkostnaden er 12%. Albatros har forventet overskudd for renter og skatt på 1 MNOK årlig i all fremtid, første gang om ett år. Selskapet har konstant kapasitet. Se bort fra skatt.
Hva er verdien av Albatros?
(a) 1.000.000 NOK
(b) 8.333.333 NOK
(c) 10.000.000 NOK
(d) 12.333.333 NOK

Her er vi i situasjon A: Uten skatt, uten gjeld
V = (OFRS) / Kt
V = 1.000.000/0,12 = 8.333.333

3. Hardwood er finansiert med 70% egenkapital og 30% risikofri gjeld. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalen har en beta på 1.14. Se bort fra skatt.
Hva er Hardwoods totalkapitalkostnad i følge Modigliani & Miller?s teori?
(a) 9,6%
(b) 12,0%
(c) 13,8%
(d) 15,4%

Her er vi i situasjon B: Uten skatt, med gjeld

Ke = Rf + [E(Rm) – Rf)*Beta
Ke = 0,04 + 0,07*1,14 = 0,12

Kt = (We*Ke)+(Wg*Kg)
Kt = 0,7*0,12 + 0,3*0,04
Kt = 9,6%

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

4. Hardwood er finansiert med 70% egenkapital og 30% risikofri gjeld. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalen har en beta på 1.14. Se bort fra skatt.
Hva er Hardwoods egenkapitalkostnad i følge Modigliani & Miller?s teori?
(a) 9,6%
(b) 12,0%
(c) 13,8%
(d) 15,4%

Egenkapitalkostnaden vil vanligvis øke med økt gjeldsgrad, (pga større risiko for eierne). Nå er det imidlertid sånn i denne oppgaven at det er risikofri gjeld, så det vil ikke påvirke egenkapitalkostnaden. Den vil være 12% slik som i oppgave 3, men vi kan regne den for syns skyld:
Ke = Ku + (Ku-Kg)*G/EK
Ke = 0,096 + (0,096-0,04)*3/7
Ke = 12%

5. Et selskap mottar et lån på 10 MNOK til 8% rente fra lokale myndigheter for å foreta en investering i lokalmiljøet. Et tilsvarende lån i finansmarkedet ville hatt en rente på 10%. Lånet er et serielån over 4 år, med etterskuddsbetaling av renter. Se bort fra skatt.
Hva er nåverdien av det subsidierte lånet?
(a) 0,20 MNOK
(b) 0,42 MNOK
(c) 0,76 MNOK
(d) 1,29 MNOK

Her må du sette opp en kontantstrøm for lånet, og neddiskontere det med r=10%

(tall i 1000 kroner)	0	1	2	3	4
Opptak/avdrag	+10.000	-2.500	-2.500	-2.500	-2.500
UB lån		7.500	5.000	2.500	0
Renter (8%)		-800	-600	-400	-200
Kontantstrøm	+10.000	-3.300	-3.100	-2.900	-2.700

Legg inn i finanskalkulatoren eller regne nåverdien manuelt, og du vil finne at NV = 415.000

6. Markedsprisen på en aksje er 75 kroner. Om ett år vil markedsprisen være enten 50 eller 100 kroner. Investor kan låne til risikofri rente på 5% for den aktuelle perioden. En kjøpsopsjon på aksjen med ett år til forfall har en innløsningskurs på 75 kroner.
Hvilken verdi har kjøpsopsjonen i dag?
(a) 0 NOK
(b) 12,90 NOK
(c) 13,69 NOK
(d) 15,97 NOK

K0 = 1/1,05 * 25*[(1,05 – 0,667)/(1,33-0,667)
K0 = 13,75 (runder til nærmeste alternativ, 13,69)

7. Markedsprisen på en aksje er 75 kroner. Om ett år vil markedsprisen være enten 50 eller 100 kroner. Investor kan låne til risikofri rente på 5% for den aktuelle perioden. En salgsopsjon på aksjen med ett år til forfall har en innløsningskurs på 75 kroner.
Hvilken verdi har salgsopsjonen i dag?
(a) 7,77 NOK
(b) 8,89 NOK
(c) 10,12 NOK
(d) 12,37 NOK

Tar utgangspunkt i salg-kjøp paritet
K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf
S0 = 13,69 – 75 + 75/1,05 = 10,12
8. Fra regnskapene til selskapene Thecno og Elnor har du følgende informasjon:

	Thecno	Elnor
Eiendeler	400	500
Egenkapital	400	250
Gjeld	0	250
E(OFRS)	40	40
E(OFS)	40	30

Selskapene betaler ikke skatt.

I følge Modigliani & Miller’s teori er markedsverdien av Thecno og Elnor i likevekt den samme, den er beregnet til 475 MNOK.
Hva er egenkapitalkostnaden i Thecno og Elnor i likevekt?
(a) 8,00% and 10,00%
(b) 8,42% and 10,57%
(c) 8,42% and 13,33%
(d) 10,00% and 10,00%

Thecno er i situasjon A. Uten skatt, uten gjeld
V = 475
Kt = Ke = E(OFRS)/V
Kt = Ke = 40/475 = 8,42%

Elnor er i situasjon B: Uten skatt, med gjeld
V = 475
G = 250,
EK = 475-250 = 225
Eiers kontantstrøm etter at rentene er betalt er 30
Ke = KS(eier) / EK
Ke = 30 / 225
Ke = 13,33%
9. NewTech har akkurat bestemt å investere 40 MNOK i et miljøvennlig prosjekt. Ved bruk av ny teknologi, vil NewTech produsere oppvaskmaskiner som har et rengjøringssystem som bruker luft istedenfor vann. Den forventede kontantstrømmen fra prosjektet er 10 MNOK pr år i 5 år. Prosjektet finansieres med 50% egenkapital og 50% gjeld. Gjelden er et serielån på 5 år med 7% rente. Selskapet betaler 28% skatt, all investorer betaler også 28% skatt. Risikofri rente er 6%, den forventede avkastningen på markedsporteføljen er 13%. Prosjektets investeringsbeta er 1.2.

Hva er nåverdien av denne investeringen hvis vi forutsetter at prosjektet er 100% egenkapitalfinansiert?
(a) – 7,2 MNOK
(b) – 6,0 MNOK
(c) 5,2 MNOK
(d) 10,0 MNOK

Her er vi i situasjon E: med toleddsskatt, uten gjeld:

Kt = Rf + [E(Rm) – Rf]*Beta
Kt = 0,06 + [0,13 – 0,06)*1,2
Kt = 14,4%

NV = -40 + 10/1,144 + …. + 10/1,144^5
NV = -6,0

10. NewTech har akkurat bestemt å investere 40 MNOK i et miljøvennlig prosjekt. Ved bruk av ny teknologi, vil NewTech produsere oppvaskmaskiner som har et rengjøringssystem som bruker luft istedenfor vann. Den forventede kontantstrømmen fra prosjektet er 10 MNOK pr år i 5 år. Prosjektet finansieres med 50% egenkapital og 50% gjeld. Gjelden er et serielån på 5 år med 7% rente. Selskapet betaler 28% skatt, all investorer betaler også 28% skatt. Risikofri rente er 6%, den forventede avkastningen på markedsporteføljen er 13%. Prosjektets investeringsbeta er 1.2.
Hva er verdien av renteskattegevinsten?
(a) 0,76 MNOK
(b) 1,05 MNOK
(c) 1,80 MNOK
(d) 2,45 MNOK

Her må vi sette opp en kontantstrøm igjen:

OBS: Jeg ser at renteskattebesparelsen har fått negativt fortegn. Det skal være positive tall.

Vi legger “kontantstrømmen” av renteskattebesparelsen inn i finanskalkulator med diskonteringsrente etter skatt: 0,07*(1-0,28) = 5,04%
Da får vi NV av renteskattebesparelse = 0,7562

11. NewTech har akkurat bestemt å investere 40 MNOK i et miljøvennlig prosjekt. Ved bruk av ny teknologi, vil NewTech produsere oppvaskmaskiner som har et rengjøringssystem som bruker luft istedenfor vann. Den forventede kontantstrømmen fra prosjektet er 10 MNOK pr år i 5 år. Prosjektet finansieres med 50% egenkapital og 50% gjeld. Gjelden er et serielån på 5 år med 7% rente. Selskapet betaler 28% skatt, all investorer betaler også 28% skatt. Risikofri rente er 6%, den forventede avkastningen på markedsporteføljen er 13%. Prosjektets investeringsbeta er 1.2.
Hva er dette miljøvennlige prosjektets justerte nåverdi?
(a) -6,76 MNOK
(b) -5,24 MNOK
(c) 5,24 MNOK
(d) 6,76 MNOK

Justert nåverdi = nåverdien av investeringen + nåverdien av finansieringen
Vi har regnet ut at nåverdien av investeringen er -6,0 (oppgave 9) og at nåverdien av finansieringen er 0,7562
Justert nåverdi = -6+0,7562 = -5,24

12. Et selskap har 3 millioner utestående aksjer. Aksjeprisen er 20 kroner pr aksje. Selskapet har en gjeld på 40 MNOK. Selskapet betaler obligasjonseierne 6% rente. Aksjene i selskapet har en beta på 1,41. Risikofri rente er 4% og markedets risikopremie er 9,5%. Selskapet betaler 28% skatt.
Hva er selskapets gjennomsnittlige kapitalkostnad (WACC)?
(a) 11,63%
(b) 12,17%
(c) 12,84%
(d) 17,40%

Bedriften er finansiert på følgende måte:
Gjeld: 40 millioner
EK: 20*3 millioner = 60 millioner
Totalkapital = 100 millioner

WACC = Ke*We + Kg*Wg*(1-Sb)

Da må vi først finne Ke
Ke = Rf + [E(Rm) – Rf]*Beta
Ke = 0,04+0,095*1,41
Ke = 17,4%

WACC = 0,174*0,6 + 0,06*0,4*(1-0,28)
WACC = 12,17%

13. Amerikanske dollar noteres i Paris til 0,7293 og i Oslo til 5,7000. Euro noteres i Oslo til 7,72000.
Hvilken mulig arbitrasjegevinst kan du oppnå hvis du har 1 millioner kroner å investere?
(a) 12.398 kroner
(b) 13.546 kroner
(c) 59.977 kroner
(d) 70.000 kroner

Okey, så:
Dollar:
Paris: EUR/USD = 0,7293
Oslo: NOK/USD = 5,70
Euro:
Oslo: NOK/EUR = 7,7200

Det gir oss en krysskurs: EUR/USD*NOK/EUR = NOK/USD = 0,7293*7,72 = 5,6302
Vi ser at dollaren er “for dyr” i Norge:

1. Kjøper Euro i Norge for 1 million til kurs 7,72: 1.000.000/7,72 = 129.534 Euro.

2. Veksler disse EUR 129.534 til USD i Paris: 129.534/0,7293 = 177.614 Dollar.

3. Vi selger USD 177.614 i Norge: 177.614*5,70 = 1.012.398

Arbitrasjegevinst: 1.012.398 – 1.000.000 = 12.398

14. Du har eksportert varer til USA og skal motta et beløp i dollar om 6 måneder. For å redusere effekten av en mulig lav dollarkurs ønsker du å benytte en valutaopsjon.
Hvilken opsjonskontrakt er det mest fornuftig å bruke?
(a) Kjøp av en dollar salgsopsjon.
(b) Kjøp av en dollar kjøpsopsjon.
(c) Salg av en dollar salgsopsjon.
(d) Salg av en dollar kjøpsopsjon.

Du ønsker å sikre deg mot en lav kurs når du skal motta dollar. Da må du kjøpe en salgsopsjon, som gir deg rett til å selge dollaren du mottar.

15. En valutatunnel består av to opsjoner med forskjellige innløsningskurser. Anta at du har solgt en kjøpsopsjon med innløsningskurs 6 (kroner pr. utenlandsk valutaenhet) og kjøpt en salgsopsjon med innløsningskurs 4, begge med forfallsdato om 3 måneder. Du skal motta 1 million i den utenlandske valutaen om 3 måneder.
Hva blir den totale kontantstrømmen du mottar hvis dagskursen om 3 måneder er henholdsvis 3, 5 og 7?
(a) 1, 0 og 0 kroner.
(b) 3, 5 og 7 kroner.
(c) 4, 5 og 6 kroner.
(d) 7, 5 og 4 kroner

Jeg skal prøve å forklare dette veldig, veldig enkelt uten å bruke figurer. Iallfall er det slik jeg tolker oppgaven:
-Du har solgt en kjøpsopsjon, som forplikter deg til å selge til 6 dersom innehaveren ønsker å kjøpe til den kursen.
-Du har kjøpt en salgsopsjon, som gir deg rett men ikke plikt til å selge for 4 dersom du ønsker det. Utstederen er forpliktet til å kjøpe.

Dersom dagskursen er 3 får du den utenlandske valutaen, og ønsker å selge til 4 fordi 4 er høyere enn dagskursen. KS: 4
Dersom dagskursen er 5, ønsker du ikke å benytte deg av salgsopsjonen, fordi du får solgt den for 5 i markedet. KS: 5
Dersom dagskursen er 7 vil du sannsynligvis måtte innfri forpliktelsene dine til innehaveren av kjøpsopsjonen. Du får valutaen og selger den for 6. KS: 6

16. Alpha er 100% egenkapitalfinansiert. Forventet avkastning på aksjene er 10%. Selskapet planlegger å låne penger og deretter kjøpe tilbake aksjer slik at gjeldsgraden (gjeld/egenkapital) blir lik 1,00. Med en gjeldsgrad på 1,00 vil lånekostnaden være 5%. Det er ingen skatter.
Hva er forventet avkastning på egenkapitalen etter tilbakekjøpet?
(a) 10,00%
(b) 13,25%
(c) 15,00%
(d) 17,75%

Vi er i univers A og går over i univers B.
I univers A: uten skatt, uten gjeld er Kt og Ke lik, og vi får oppgitt at avkastningen på aksjene = 0,10.
Ke = Kt = 0,10

I univers B er gjeldsgraden 1 (Gjeld/EK = 1). Det betyr at det er like mye gjeld som egenkapital, altså 50/50.
I univers B finner vi Ke slik:
[Ke = Kt + (Kt – Kg)*G/EK[
Ke = 0,10 + (0,10-0,05)*1 = 15%

17. Arrow er 100% egenkapitalfinansiert og har en markedsverdi på 100 millioner dollar. Egenkapitalbetaen til selskapet er 0,50. Selskapets ledelse planlegger å endre kapitalstrukturen til selskapet ved å låne 40 millioner dollar (risikofri gjeld) og deretter bruke lånet samt 10 millioner dollar i kontanter for å kjøpe tilbake aksjer i selskapet.
Hva blir selskapets egenkapitalbeta etter tilbakekjøpet? Forutsett perfekte kapitalmarkeder.
(a) 0,50
(b) 0,75
(c) 0,90
(d) 1,00

Selskapet tilbakekjøper aksjer for 10 millioner. Dette reduserer antallet utestående aksjer i markedet. Tilbakekjøp av aksjer brukes ofte som en skatteeffektiv måte å overføre kontanter til aksjeeierne på, snarere enn å utbetale utbytte. I balansen føres tilbakekjøpte aksjer under egne aksjer i form av et negativt tall. Dette vil påvirke selskapsverdien, men ikke aksjeverdien. Hvorfor?

Så til oppgaven:

I univers A: uten skatt, uten gjeld er beta til EK og beta til TK den samme: βt = βe = 0,5

Dersom de tar opp gjeld går de over i univers B: uten skatt, med gjeld.
Dette vil påvirke balansens høyreside:
Egenkapitalen vil reduseres fra 100 til 50 (100 – gjeld – tilbakekjøpte aksjer)
Gjeld vil øke fra 0 til 40
Sum EK + G = 90, som er den nye verdien til selskapet

Da finner vi βe:
[βe = βt + (βt – βg)*G/EK]
– Betaen til totalkapitalen vil ikke ha forandret seg.
– Betaen til gjeld er 0, da gjelden er risikofri (jfr. oppgaveteksten)
βe = 0,5+(0,5-0)*40/50
βe = 0,9

18. Hvilket av følgende utsagn er korrekt?
(a) Justert Nåverdi er bedre enn Egenkapitalmetoden og Totalkapitalmetoden dersom gjeldsgraden er konstant.
(b) Ved bruk av Justert Nåverdi diskonteres kontantstrøm ved 100% egenkapitalfinansiering etter skatt med egenkapitalkostnaden ved 100% egenkapital.
(c) Ved bruk av Egenkapitalmetoden diskonteres kontantstrøm til eiere etter skatt med egenkapitalkostnaden ved 100% egenkapital.
(d) Totalkapitalmetoden anvendes oftere enn Egenkapitalmetoden fordi det er enklere å beregne totalkapitalkostnaden enn egenkapitalkostnaden ved 100% egenkapital.

Justert nåverdi = nåverdien av investeringen + nåverdien av finansieringen
Dersom vi har en kontantstrøm på et prosjekt 100% finansiert av egenkapital, vil man bruke egenkapitalkostnaden (ved 100% EK) som diskonteringsrente.

19. Du tror at volatiliteten i aksjekursen vil være lavere enn implisitt volatilitet på opsjoner i aksjen.
Hvilken strategi vil du anbefale (innløsningskursen for opsjonene er lik dagens aksjekurs)?
(a) Selg en kjøpsopsjon og selg en salgsopsjon.
(b) Selg en kjøpsopsjon og kjøp en salgsopsjon.
(c) Kjøp en kjøpsopsjon og kjøp en salgsopsjon.
(d) Kjøp en kjøpsopsjon og selg en salgsopsjon.

Slik jeg har skrevet i et tidligere innlegg så har volatilitet (svingninger, standardavvik, risiko) innvirkning på derivatpriser. En opsjon er et derivat. Derivater blir mer verdt jo mer usikkerhet og jo større svingninger det er i det underliggende verdiobjektet. Det betyr at dersom du sitter på opsjoner, og du tror at den volatiliteten som er priset inn i den er større enn den reelle, så vil markedet snart fange opp dette og prisen på opsjonene vil falle. Du bør derfor selge alle opsjonene du har.

20. Bella har en gjeldsgrad (gjeld/egenkapital) lik 1,00 og en egenkapitalbeta på 1,50. Gjeldsbetaen er 0,30. Selskapsskattesatsen er 30%. Anta at Modligiani-Miller forutsetninger holder.
Hva er beta ved 100% egenkapitalfinansiering?
(a) 0,90
(b) 1,01
(c) 1,26
(d) 1,50

Vi er her i univers D: med ettleddsskatt, med gjeld.

Investeringsbetaen finner vi slik:
βI = βe*

βI = 1,01

21. Happy ASA har en egenkapitalkostnad på 10% ved 100% egenkapitalfinansiering. Selskapets lånekostnad er 7%. Selskapsskattesatsen er 30%, mens personbeskatning på inntekt fra egenkapital er 20%. Personbeskatning på renteinntekter utgjør 20%. Selskapets ledelse ønsker å undersøke virkningen av en mulig endring i kattesystemet. Noen politikere har foreslått å øke personbeskatningen på renteinntekt til 50% for å få et nøytralt skattesystem.
Hvilket av følgende utsagn er korrekt dersom det blir en slik fremtidig endring i skattesystemet?
(a) Selskapet vil ikke tjene på å ha mer gjeld dersom skattesystemet endres.
(b) Selskapet vil tjene på å ha mer gjeld dersom skattesystemet endres.
(c) Selskapet vil tjene på å ha mer gjeld med dagens skattesatser, men vil tjene på å ha mindre gjeld med de foreslåtte skattesatsene.
(d) Både (a) og (c).

Vi regner ut n* for de to scenarioene. n* viser som kjent netto skattefordel ved å erstatte en dividendekrone med en gjeldskrone.

n* = (1-Sk) – (1-Sb)*(1-Se)
n* i dag = (1-0,2) – (1-0,3)*(1-00,2) = 0,24

N* dersom endring = (1-0,5) – (1-0,3)*(1-0,2) = -0,04

Det vi ser er at n* blir negativ ved en endring, altså betyr det at det ikke vil være noen skattefordel ved å erstatte en dividendekrone med en gjeldskrone. I dag er den positiv, som betyr at selskapet får en økt skattefordel ved å oppta mer gjeld.

22. Et selskaps aksjekurs er 75 kroner i begynnelsen av året. Ved utgangen av året vil aksjekursen enten være 50 kroner eller 100 kroner. Investorer kan låne og plassere til risikofri rente på 5% for perioden. Både en salgs- og kjøpsopsjon på aksjen med ett år til forfall har innløsningskurs på 80 kroner. En investor har 100 aksjer i selskapet. Han ønsker å sikre seg mest mulig mot endringer i aksjekursen.
Hvilket av følgende utsagn er korrekt?
(a) Investoren kan sikre aksjeposisjonen ved å selge kjøpsopsjoner på 250 aksjer. Prisen for kjøpsopsjoner på 250 aksjer er 2.738 kroner.
(b) Investoren kan sikre aksjeposisjonen ved å selge kjøpsopsjoner på 250 aksjer. Prisen for kjøpsopsjoner på 250 aksjer er 1.750 kroner.
(c) Det er umulig å bruke salgsopsjoner for å sikre aksjeposisjonen.
(d) Investoren kan sikre aksjeposisjonen ved å kjøpe 167 salgsopsjoner. Kostnaden ved denne strategien er 1.750 kroner.

Eier 100 aksjer:

Sikringsforholdet (m):
[m = A0*(ø-n) / (Kø – Kn)]
m = 75*(1,33-0,67) / (20-0)
m = 2,5

Tolkningen av m:
– Vi må selge 2,5 kjøpsopsjoner pr eid aksje for å sikre oss.

K0 = 1 / 1,05 * [20*(1,05-0,67) / (1,33-0,67)]
K0 = 10,952524

100 eide aksjer, sikringsforhold 2,5 = 100*2,5 = 250 kjøpsopsjoner til pris 10,952524 – totalt: 2738
23. Agri Inc er tilbudt et 5-års lån på 100 millioner kroner med en årlig effektiv rente på null prosent (pålydende tilbakebetales på slutten av år 5). Effektiv markedsrente på tilsvarende lån er 10%. Det er ingen skatter.
Hva er nåverdien til lånet?
(a) 23,33 millioner kroner
(b) 26,54 millioner kroner
(c) 32,68 millioner kroner
(d) 37,91 millioner kroner

Her får vi en kontantstrøm som ser slik ut:

0	…	5
100		-100

Vi må neddiskontere den til år 0 med den effektive markedsrenten på tilsvarende lån.
Nåverdien = +100 – 100/1,1^5
NV = 37,91

24. Et selskap har 3 millioner aksjer utestående med markedskurs 20 kroner/aksje og med en beta lik 1,4. Egenkapitalens bokverdi er 55 millioner kroner. Selskapet har i tillegg utstedt 50 millioner kroner i langsiktig gjeld, som for tiden omsettes til 80% av pålydende. Gjeldens effektive årlige avkastning før skatt er 10%. Risikofri rente er 6% og markedets risikopremie er 5%. Selskapet betaler 30% inntektsskatt.
Hva er selskapets veide gjennomsnittlige kapitalkostnad?
(a) 8,3%
(b) 10,1%
(c) 10,6%
(d) 11,8%

Veid gjennomsnittlig kapitalkostnad (Weighted Average Cost of Capital – WACC)

Selskapet har 3 millioner utestående aksjer med markedskurs 20 kroner. Da er egenkapitalen 20*3 millioner = 60 millioner.
Selskapets gjeld er 80% av 50 millioner (markedsverdi av gjeld), som er 40 millioner
Selskapets totalkapital er derfor 100 millioner.
Vekting av EK (We) blir 60/100=0,6
Vekting av gjeld (Wg) blir 0,4

WACC (Kt) = Ke*We + Kg*(1-s)*Wg

Finner Ke:
Ke = Rf + Risikopremie*beta
Ke = 0,06 + 0,05*1,4
Ke = 13%

Kt = 0,13*0,6 + 0,10*(1-0,3)*0,4 = 10,6%

25. Du vurderer en kjøpsopsjon (call) og en salgsopsjon (put) på samme underliggende aksje. Opsjonene har samme løpetid.
For at kjøps- og salgsopsjonens kurs skal utvikle seg i motsatt retning må:
(a) Prisen på den underliggende aksjen øke.
(b) Opsjonenes tid til forfall må øke.
(c) Volatiliteten til den underliggende aksjen må øke.
(d) Både opsjonenes tid til forfall og volatiliteten til den underliggende aksjen må øke.

Dersom prisen på den underliggende aksjen øker, så vil det føre til at salgsopsjonen (din rett til å selge aksjen til innløsningskurs) vil tape seg i verdi, fordi gevinsten din ved å kunne selge en aksje til innløsningskurs vil reduseres jo nærmere markedsprisen er innløsningskursen. Salgsopsjonen din har bare verdi dersom innløsningskursen er høyere enn markedskursen.
Tilsvarende vil din kjøpsopsjon styrke seg i verdi, fordi gevinsten din ved å kunne kjøpe en aksje til innløsningskurs vil øke jo høyere markedskursen er i forhold til innløsningskursen. Kjøpsopsjonen din har bare verdi dersom innløsningskursen er lavere enn markedskursen.

Opsjonens tid til forfall vil påvirke begge opsjonene i samme retning (økt verdi ved økt tid til forfall). Det samme gjelder volatilitet (økt verdi ved økt volatilitet).

26. Den risikofrie årsrenten er 6% i USA og 3% i eurosonen. Dagskursen er 1 EUR = 1,35 USD.
Hva er 12 måneders terminkurs mellom EUR og USD dersom arbitrasjegevinster ikke er mulig?
(a) 1 EUR = 1,3893 USD
(b) 1 EUR = 0,7198 USD
(c) 1 EUR = 1,3118 USD
(d) 1 EUR = 1,4739 USD

En terminkontrakt har mye til felles med opsjoner. Begge er finansielle instrumenter hvor verdien avhenger av et underliggende objekts verdi (et derivat). Begge instrumentene innebærer at to parter avtaler en fremtidig transaksjon, og at betingelsene for transaksjonen avtales i dag. Forskjellen er at både selger og kjøper (utsteder og innehaver) forplikter seg til å gjennomføre transaksjonen, mens vi husker at det for opsjoner er innehaveren som velger hvorvidt vedkommende ønsker å benytte seg av avtalen. Med mindre spotkurs ved innløsningstidspunktet er lik terminkursen, vil en av partene ha en gevinst på kontrakten, mens den andre parten vil ha en tilsvarende ugunst. Summen av gevinst og tap vil være null, og vi sier derfor at det er et “null-sum-spill”.

[Terminkurs = Spot * (1+rente i hjemlandet) / (1+rente i utlandet)]
Terminkurs = 1,35 * (1,06 / 1,03)
Terminkurs = 1,389

27. Dagskursen mellom enkelte valutaer er som følger:
1 EUR = 1,3500 USD, 1 EUR = 0,7050 GBP, 1 EUR = 0,9200 CHF.
Hva er dagskursen mellom amerikanske dollar og sveitsiske franc, samt mellom sveitsiske franc og britiske pund dersom det ikke foreligger noen arbitrasjemuligheter?
(a) 1 CHF = 1,2420 USD, 1 CHF = 0,6486 GBP
(b) 1 CHF = 0,6815 USD, 1 CHF = 1,3050 GBP
(c) 1 CHF = 0,8051 USD, 1 CHF = 1,5418 GBP
(d) 1 CHF = 1,4673 USD, 1 CHF = 0,7663 GBP

Så:
EUR/USD = 1,3500 (betaler 1,35 USD for en euro— 1,35 dollar gir én euro)
EUR/GBP = 0,7050
EUR/CHF = 0,9200 (betaler 0,9200 franc for en euro – 0,9200 franc gir én euro]

Vi vet vi betaler 0,9200 CHF for en EUR, som betyr at vi betaler 1/0,9200 = 1,0870 EUR for en CHF –> (CHF/EUR=1,0870)

CHF/USD = EUR/USD * CHF/EUR
1,35*1,0870 = 1,4673

Dersom det ikke foreligger arbitrasjemuligheter må en CHF koste 1,4673 USD

CHF/GBP = EUR/GBP * CHF/EUR
CHF/GBP = 0,7050*1,0870
CHF/GBP = 0,7663

Dersom det ikke foreligger arbitrasjemuligheter må en CHF koste 0,7663 GBP

Vanskelig å forstå? Enig. Det er kanskje ikke lett å se logikken, og det er lett at det kan gå i surr, men jeg skal forsøke å forklare hvordan jeg tenker.

Jeg skal finne ut hvor mange dollar jeg må betale for en sveitsisk franc (CHF/USD = dollar pr sveitsiske franc)
Da må jeg finne en krysskurs.
– EUR/USD forteller hvor mange dollar jeg må betale for en euro)
– CHF/EUR forteller hvor mange euro jeg betaler for en sveitsisk franc)
– Når jeg tar EUR/USD * CHF/EUR finner jeg en krysskurs. Du kan se for deg at du først veksler om fra dollar til euro til kurs 1,3500, så fra euro til sveitsiske franc til kurs 1,0870. Krysskursen viser derfor hva kursen må være for at du ikke skal få noen gevinst ved å veksle fra sveitsiske franc til dollar igjen.

Talleksempel:
#1: Du har 1 million dollar. Du veksler dem til euro: 1.000.000/1,35 = 740.740,741 euro.

#2: Du har nå 740.740,741 euro. Du veksler det til sveitsiske franc: 740.740,741/1,0870 = 681.454,224

#3.1: Du har nå 681.454,224 sveitsiske franc. Du vet du betaler 1,4673 dollar for 1 franc, det betyr at du betaler 1/1,4673 = 0,6815239 franc for en dollar. Du veksler franc til dollar: 681.454,224/0,6815239 = ca 1.000.000 dollar (litt avvik pga avrundende desimaler)

#3.2 Du kan også tenke slik: Du har nå 681.454,224 sveitsiske franc. Hva må kursen være for at du skal kunne veksle dette tilbake til 1.000.000 dollar?
1.000.000/681.454,224 = ca 1,4673

28. Laks AS har en gjeldsgrad (gjeld/egenkapital) på 0,8. Egenkapitalbetaen er 2,0, mens gjelden er risikofri. Selskapet oppnår hvert eneste år en kontantstrøm før skatt på enten 1.000.000 eller 500.000 med lik sannsynlighet. Risikofri rente er 3%, markedets risikopremie er 5% og selskapets skattesats er 20%.
Hva er totalverdien av Laks?
(a) 923.455
(b) 7.238.606
(c) 9.048.257
(d) 13.274.336

Her er vi i univers D: med ettleddsskatt, med gjeld.
Her har vi ikke oppgitt gjeld, EK eller totalkapital i kroner, men det trenger vi heller ikke. Vi må bare vite vektingen.
– Vi vet at gjeldsgraden er 0,8, altså at G/EK = 0,8.
– Det betyr at G/EK = 4/5. —> G= 4, EK = 5
– Da må G+EK være 4+5 = 9
– Da vet vi at vektingen av G = 4/9 og at vektingen av EK = 5/9

Vi vet at Ke = Rf + Risikopremie*beta
Ke = 0,03+0,05*2 = 13%

Kt = Ke*We + Kg*Wg(1-Sb)
Kt = 0,13*5/9 + 0,03*4/9*(1-0,2) = 8,29%

E(OFRS) = 1.000.000*0,5 + 500.000*0,5
E(OFRS) = 750.000
Eiernes kontantstrøm: 750.000*(1-0,2) = 600.000

Totalverdien av selskapet (V)
600.000/0,0829 =7.237.635,71

29. Hval ASA er et børsnotert selskap med en gjeldsgrad (gjeld/egenkapital) på 1. Det forventes at selskapet vil utbetale en dividende på kr 5 ved årets slutt (du er nå ved årets begynnelse), for deretter å øke med 2% årlig i overskuelig fremtid. Dagens aksjekurs i Hval er kr 25, og gjeldsbetaen er 0,5.
Krill AS er ikke børsnotert. Krill har en gjeldsgrad på 1,5 og forventes å utbetale en dividende på kr 10 per aksje ved årets slutt, men en etterfølgende årlig dividendevekst på 4%. Gjeldskostnaden i Krill er 5%.
Det er ingen skatt, risikofri rente er 1% og markedets risikopremie er 5%. Hval og Krill er i samme bransje med sammenlignbar eiendelsrisiko.
Hva er aksjekursen i Krill i likevekt?
(a) kr 45,45
(b) kr 49,08
(c) kr 55,56
(d) kr 114,29

Hval ASA har en gjeldsgrad på 1, som vil si at selskapet er finansiert med 50% EK og 50% gjeld.

Verdien pr. aksje (P0) kan estimeres ved å multiplisere første års forventede dividende (E(D1)), egenkapitalkostnaden (Ke) og vekst (v). Slik:

P0 = E(D1) / (Ke – v)
Vi kan nå bruke denne formelen til å finne Ke
25 = 5 / (Ke-0,02)
Ke = 22%

Da kan vi finne Kg:
Kg = risikofri rente + markedets risikopremie*gjeldsbeta
Kg = 0,01 + 0,05*0,5 = 3,5%

Da kan vi finne Kt. Grunnen til at vi vil det er at vi forutsetter at denne er den samme i Krill AS.
Kt = 0,22*0,5 + 0,035*0,5 = 0,1275

Nå kan vi bruke den samme formelen på Krill AS:
P0 = E(D1) / (Ke – v)

Vi må bare finne Ke først. Vi vet at gjeldsgrad = 1,5, som betyr at G/EK = 1,5. 3/2 =1,5. Da vet vi at G=3, EK=2, G+EK=5
Kt = Kg*Wg + Ke*We
0,1275 = 0,05*3/5 + Ke*2/5
Ke = 24,38%

P0 = E(D1) / (Ke – v)
P0 = 10 / (0,2438-0,04) = 49,068

30. Dagens aksjekurs i Alpha er kr 150. Om 12 måneder kan aksjekursen enten stige til kr 180 eller falle til kr 140. Prisen på en salgsopsjon (put) på aksjen i Alpha med innløsningskurs kr 160 og forfall om 12 måneder er kr 10,55.
Hva er 12-måneders risikofri rente?
(a) 3,50%
(b) 5,20%
(c) 8,60%
(d) 10,67%

Okey. Denne er ikke veldig hyggelig, men vi får sett på en del sammenhenger når vi løser den. La oss gå i gang.

Vi husker denne formelen fra en tidligere oppgave:
[m = A0*(ø-n) / (Kø – Kn)]
Denne brukte vi til å konkludere med hvor mange kjøpsopsjoner vi trengte pr. eid aksje for å sikre oss. Når vi skal bruke den på å regne hvor mange salgsopsjoner vi trenger for å sikre oss, må vi snu den (altså 1/m). Da blir den sånn:
m = (Kø-Kn) / A0*(ø-n)
m = 0-20 / 150*(1,2-0,9333)
m = -0,5

Vi kan bruke følgende sammenheng for å finne Rf:
I = Kn – A0*n*m / 1+Rf
I = 20 – (150*0,93*(-0,5)) / 1+Rf
I = 20 + 70 / 1+Rf

S0 = A0*m+I
10,55 = 150(-0,5) + I
I = 85,55

I = 20 + 70 / 1+Rf
85,55 = 20+70 / 1+Rf
Rf = 5,20%

Det var det eksamenssettet. Følg med for mer, og si gjerne fra hvis jeg har gjort noe feil 🙂

Posted on 25.11.2016

Finansiell styring – gjeldsfinansiering og verdi

I dette faget opererer vi med 6 forskjellige situasjoner – eller “univers” som jeg gjerne kaller det. Gjeldssituasjon og skattesituasjon er ulik i de seks universene, som påvirker verdien av selskapet. Hvilke formler og sammenhenger vi bruker vil variere fra univers til univers. I innleggene for dette faget refererer jeg til disse universene, som er:

A: Uten skatt, uten gjeld
B: Uten skatt, med gjeld
Felles for A og B: kapitalstrukturen er irrelevant i en verden uten skatt.

C: Med ett-leddsskatt, uten gjeld
D: Med ett-leddsskatt, med gjeld
Felles for C og D: ønsker maks gjeldsgrad, da selskapsverdien øker med nåverdien av renteskattebesparelsen.

E: Med to-leddsskatt, uten gjeld
F: Med to-leddsskatt, med gjeld
Her vil verdien av n* avgjøre hvilken finansiering som vil gi høyest verdi for selskapet.

I hvert av tilfellene ser vi for oss et forventet overskudd før renter og skatt: E(OFRS) = 1000
Vi forutsetter at alt overskudd betales som utbytte.
E(OFRS) skal fordeles på:
-Eiere
-Kreditorer
-Staten

Vi forutsetter følgende balanser:

Uten gjeld:

Aktiva	Passiva
Eiendeler: 5′	Egenkapital: 5′
	Gjeld: 0

Med gjeld:

Aktiva	Passiva
Eiendeler: 5′	Egenkapital: 2′
	Gjeld: 3′

Gjeldsrente: 0,08

Skattesatser:
Selskapsskatt (Sb) = 0,25
Kreditorskatt (Sk) = 0,25
Investorskatt (SEd) = 0,11

Sammendrag av formler og sammenhenger for de forskjellige universene kan du finne i dette dokumentet:
Gjeldsfinansiering og verdi

Eksempel, som viser fremstillingen av univers A:

A: Uten skatt, uten gjeld

Posted on 20.11.201619.04.2022

Finansiell styring – innleveringsoppgave høst 2016

Nå mine venner. Dette innlegget er way overdue, jeg vet. Jeg har hatt mye å gjøre med verv og ikke minst ferdigstillelse av strategioppgaven.

NOK UNNSKYLDNINGER, HÆ? La oss komme igang! Rop ut om noe er feil eller uklart.

OBS: Når jeg prater om “univers A, B, C” osv, refererer jeg til de ulike universene av skatt/gjeld. Du bør lese dette korte innlegget før du setter i gang:
Gjeldsfinansiering og verdi

Litt teori først. En opsjon er et derivat. Et derivat er et finansielt instrument hvor verdien av instrumentet avhenger av verdien et underliggende objekt – f.eks. en aksje. En opsjon gir eieren (innehaveren) av opsjonen en rett, men ikke en plikt, til å kjøpe (kjøpsopsjon) eller selge (salgsopsjon). Du har et valg: en “option”. Selgeren (utstederen) av opsjonen har derimot en plikt til å innfri opsjonen. Altså:

	Kjøper (innehaver)	Selger (utsteder)
Kjøpsopsjon	Har rett, men ikke plikt, til å kjøpe	Har plikt til å selge
Salgsopsjon	Har rett, men ikke plikt, til å selge	Har plikt til å kjøpe

Et eksempel. Du eier noen aksjer i Statoil. Statoil-aksjen i dag ligger på 132 kroner. Jeg utsteder en salgsopsjon som gir deg retten til å selge en Statoil-aksje til meg for 140 kroner om 3 måneder. Hvis aksjekursen forholder seg i ro, vil du etter 3 måneder kunne selge en aksje for 8 kroner over markedsverdi. Opsjonen er da lønnsom å bruke, og vi sier at den er “in the money”. Hvis prisen på Statoil-aksjen på den annen side stiger til 145 kroner, vil du tjene mer på å selge aksjene dine i markedet enn ved å benytte deg av salgsopsjonen. Ettersom du bare har en rett – men ikke en plikt – til å selge, kan du bare la være å benytte deg av opsjonen. Du har da bare tapt det du betalte for opsjonen i utgangspunktet. Opsjonen er ikke lønnsom å utøve, og vi sier at den er “out of the money”.

Oppgave 1

Aksjene i selskapet Aramas ASA omsettes i dag for 75 kroner per aksje. Det omsettes også kjøps- og salgsopsjoner på aksjene i Aramas med forfall om tre måneder og innløsningskurs på 75 kroner. Det forventes at markedsverdien av aksjen er enten 90 kroner eller 75 kroner om tre måneder. Risikofri rente er 4% per år.

(a) Hva er kjøpsopsjonens verdi i dag?

I eksemplet i teorigjennomgangen over er det lett å se at verdien av salgsopsjonen på innløsningstidspunktet er 140-132 = 8. Hva opsjonsverdien er 3 måneder frem i tid er ikke like lett å se. Legg merke til at risikofri rente er oppgitt pr. år å være 4%, så med andre ord 4/12 = 0,33% hver mnd, altså 1% pr kvartal.

K0 = 1/(1+0,01) * 15 * (1,01-1)/(1,20-1)
K0 = 0,9900990*15*0,05
K0 = 0,7425743

(b) Hva er salgsopsjonens verdi?

S0 = 0,7425743 – 75 + 75/1,01
S0 = 0

Dette svaret kommer vel kanskje ikke som noen bombe. Opsjonen gir deg muligheten til å selge en aksje for 75 kroner etter tre måneder. Aksjekursen vil enten være 75 eller 90, som betyr at du kan selge aksjen til nøyaktig samme pris (75) eller en betraktelig høyere pris (90) i markedet, som betyr at opsjonen ikke gir noen (mer)verdi, som betyr at opsjonsverdien er null. Hvis innløsningskursen er lik markedskurs sier vi at opsjonen er “at the money”.

Du har stor tro på at markedet vil prise aksjene i Aramas ASA til 90 kroner om tre måneder, og bestemmer deg for å investere i selskapet. Du har ingen penger, men kan låne penger i banken til risikofri rente. Du kan enten låne penger til å kjøpe 1000 aksjer i dag eller låne penger og kjøpe 1000 kjøpsopsjoner i dag med innløsningskurs på 75 kroner.

(c) Vis kontantstrømmen for de to alternativene i dag og om 3 måneder.
Antar at lånerenter blir betalt samtidig som lånet blir tilbakebetalt, ettersom oppgaven ber oss om å vise kontantstrømmen i dag og om 3 måneder (og ikke for månedene mellom.) Antar at aksjene selges ved innløsningstidspunkt i alternativ 1. Antar også at i alternativ 2 skjer oppgjøret på en sånn måte at vi ikke trenger å ta opp nytt lån (f.eks. at du shorter aksjen, bruker pengene på å innløse opsjonen, og kjøper tilbake aksjene igjen samme dag (“intradag”), som ikke utløser renter/avgifter, eller at utsteder av opsjonen bare betaler deg mellomlegget mellom innløsningskursen og markedsverdien på aksjen).

(d) Hvilket alternativ velger du? Forklar hvorfor.
I utgangspunktet har de to alternativene identiske nettokontantstrømmer, og samme nåverdi. Ved å kjøpe aksjen og selge den etter tre måneder får du hele gevinsten fra verdiøkningen selv. Ved å kjøpe opsjoner vil noe av verdiøkningen “gå tapt” i form av premie til utsteder. I dette tilfellet blir mergevinsten fra alternativ 1 “spist opp” av den ekstra rentekostnaden. Noen aspekter å tenke på da er kanskje:
– Er det tilrådelig å låne 75.000 for å kjøpe aksjer?
– Høyere rente på alternativ 1 gir skattefordel mot alternativ 2.
– Risiko. Riktignok er det ingen risiko i denne oppgaven i så måte. Hvis aksjekursen forblir 75, vil du i alternativ 1 ha tapt de 750 kronene i renter. I alternativ to vil du ha tapt 742,57 kroner i opsjonspremie og 7,43 kroner i renter som også blir 750 kroner.

Hva ville jeg valgt? Jeg ville nok kjøpt aksjene, fordi det er mindre stress.

(e) Hva er det som avgjør kjøpsopsjonens verdi i tillegg til dagens aksjekurs?

– Volatilitet (svingninger, standardavvik) i aksjekursen øker verdien av opsjonen, fordi den gir mindre risiko enn en aksje som svinger mye.
– Tid til forfall. Jo lengre tid det er til forfall, jo større er sjansen for at opsjonen ved forfall er lønnsom å benytte seg av (“in the money”). Det gir også mening at en rett (uten plikt) er mer verdt jo lengre du har retten.
– Innløsningskurs. Verdien av kjøpsopsjoner avtar med økende innløsningskurs, fordi jo høyere innløsningskursen er, jo mindre er sannsynligheten for at aksjekursen ved forfall er høyere enn innløsningskursen.
– Risikofri rente. Jo høyere rente, jo lavere nåverdi av innløsningskursen.

Oppgave 2

To selskaper, Oljeutstyr ASA og Oil-Ex ASA, er helt like bortsett fra at Oljeutstyr er 100% egenkapitalfinansiert med en totalkapitalkostnad på 10%. Oil-Ex har en gjeldsgrad på 1. Oil-Ex har 5 millioner kroner i gjeld og en gjeldskostnad på 5%. Se bort fra skatt.

(a) Hva er egenkapitalkostnaden i de to selskapene?

I en bedrift som er 100% finansiert av egenkapitalen vil alltid totalkapitalkostnaden og egenkapitalkostnaden være den samme. Hvorfor? Fordi totalkapital er summen av egenkapital og gjeld, så hvis selskapet bare har egenkapital er totalkapitalen lik egenkapitalen.

Vi vet derfor at egenakpaitalkostnaden i Oljeutstyr = 10%

Vi vet også at totalkapitalkostnaden er uavhengig av gjeldsgraden, altså vet vi at ettersom de to selskapene er helt like bortsett fra måten de er finansiert på, er totalkapitalkostnaden i Oil-Ex ASA også 10%. Da kan vi bruke brekkstangformelen f.eks:

[Ke = Kt + (Kt – Kg)*G/EK]

Ke = 0,10 + (0,10-0,05)*1 = 0,15 = 15%

(b) Forklar hvorfor det er forskjell på egenkapitalkostnaden i de to selskapene.

I Oljeutstyr er hele selskapet finansiert av egenkapital. I Oil-Ex har imidlertid selskapet forpliktelser til sine långivere som skal ha sine renter og avdrag før eierne får det som eventuelt måtte bli til overs. Dette betyr at risikoen for eierne øker, som betyr at egenkapitalkostnaden også øker.

(c) Forventet overskudd før renter er 1 million kroner i begge selskapene, hva er verdien av egenkapitalen i de to selskapene?

Verdien av egenkapitalen finner vi ved å ta forventet overskudd etter renter og dele på egenkapitalkostnaden.

Oljeutstyr: [EK = E(OER)/Ke]—> 1.000.000 / 0,10 = 10.000.000

Oil-Ex: EK = (1.000.000-(5.000.000*0,05)) / 0,15 = 5.000.000

(d) Hva er totalverdien av de to selskapene?

I dette faget bruker vi en metode for verdsetting av selskaper som kalles “Enterprise Value” (EV)-metoden. Den baserer seg på at man ved oppkjøp ikke bare kjøper selskapets verdier, men også dens gjeld, penger og pengeekvivalenter. Selskapsverdien er beregnet som:

markedsverdi + gjeld – cash

Grunnen til at man trekker fra cash er at disse vil være tilgjengelig etter oppkjøpet for å betale ned gjeld eller lignende. Jeg tror ikke vi kommer til å få en oppgave på eksamen hvor man trenger å ta hensyn til cash, men jeg nevner det likevel. Markedsverdi (market cap) er som vi vet prisen pr aksje ganget med antall utestående aksjer.

For Oljeutstyr som ikke har noe gjeld blir EV = markedsverdi –> EV = EK –> EV=10.000.0000

For Oil-Ex som har gjeld blir EV = markedsverdi + gjeld –> 5.000.000 + 5.000.000 = 10.000.000

Forenklet kan vi se at verdien av et selskap ikke avhenger av finansieringen i et univers uten skatt.

Myndighetene bestemmer at Oljeutstyr ASA og Oil-Ex må betale 28 % selskapsskatt. Se bort fra investor- og kreditorskatt.

(e) Hva er totalverdien av Oljeutstyr og av Oil-Ex nå når de betaler skatt?

Oi, her har vi fått innført skatt. Det går bra. Vi må bare vite at:
#1: Skatten vil redusere forventet overskudd
#2: Skatten vil føre til en skattebesparelse på rentene våre (renteskattebesparelse)

Vi bruker følgende sammenhenger.:

Verdi for selskap uten gjeld = [E(OERS) / Ke]

Verdi for selskap med gjeld = Verdi for selskap med gjeld + Pålydende Gjeld * Skattesats –> [Vm = Vu + PG*Sb]

Med våre tall, og prøv å se effekten av skatten i de to selskapene. :

Oljeutstyr: Vu = 1.000.000*(1-0,28) / 0,10 = 7.200.000
Her ser vi at skatten fører til et lavere forventet overskudd.

Oil-Ex: Vm = 7.200.000+(5.000.000*0,28) = 8.600.000
Her ser vi at skatten først fører til et lavere forventet overskudd, men at vi på grunn av renteskattebesparelsen får en høyere forventet kontantstrøm, og derfor høyere selskapsverdi.

Oppgave 3

(a) Anta at vi har følgende markedskurser og rentesatser: (Alle rentene er perioderenter).

Spot NOK/USD: 8,00
Rentesats NOK plassering 6 mnd.: 2,10 %
Rentesats NOK lån 6 mnd.: 2,15 %
Rentesats USD plassering 6 mnd.: 1,00 %
Rentesats USD lån 6 mnd.: 1,20 %

I. Hva blir 6 måneders terminkurs for en norsk eksportør hvis det ikke er noen arbitrasjemulighet?

II. Hva blir 6 måneders terminkurs for en norsk importør hvis det ikke er noen arbitrasjemulighet?

Her bruker vi følgende sammenheng.
På I.: Terminkurs for eksportør = Spot * (1+plasseringsrente i hjemlandet) / (1+lånerente i utlandet)
På II: Terminkurs for importør = Spot * (1+lånrente i hjemlandet) / (1+plasseringsrente i utlandet)

Med våre tall:

I: 8*(1+0,021) / (1+0,012) = 8,07
II: 8* (1+0,0215) / (1+0,01) = 8,09

(b) En norsk importør har gjort en avtale om levering av et vareparti fra en tysk leverandør på 1 millioner euro med levering om 2 måneder og 1 måneds betalingsutsettelse. Importøren har mottatt følgende opplysninger fra sin bankforbindelse:

(Alle rentene er periode renter).
Spot NOK/EUR: 9,00
Termintillegg 3 måneder: 3,56 øre
3 måneders lånerente NOK: 1,20 %
3 måneders plasseringsrente EUR: 1,00 %
Kjøpsopsjoner EUR 3 måneder (innløsningskurs = terminkurs) har premie 1,5%.

Importøren vurderer å terminsikre den åpne posisjonen, eventuelt å benytte en valutaopsjon.

Spotkurs om 3 måneder blir:
8,9 eller 9,0 eller 9,1 eller 9,2

Alle med like stor sannsynlighet. Hva blir importørens kontantstrøm for de tre alternativene (åpen, termin, opsjon) om 3 måneder?

(Åpne bildet i ny fane dersom ikke hele teksten vises)

c) Hva er fordelene/ulempene med terminsikring fremfor bruk av opsjon?

En fordel er at man kan redusere risiko for valutasvingning. Som jeg nevnte avtales den valutakursen man skal benytte for den fremtidige transaksjonen allerede i dag, slik at risikoen for svingninger ikke påvirker noen av partene. En annen fordel er at man slipper å betale en premie for å inngå kontrakten, slik man må med opsjoner. Dette er en ren kostnad man betaler for fleksibiliteten en opsjon innebærer, men den slipper man å betale ved inngåelse av terminkontrakt. En vanlig opsjon er dessuten mye mer standardisert enn en terminkontrakt, som man kan tilpasse mer etter behov.

Jeg legger ved denne lille sammenhengen mellom paritetene, som noen kanskje har sett før, hvis den kan være til hjelp:

Oppgave 4

Selskapet Admiral ASA er finansiert med egenkapital og gjeld.

(a) Hva viser skatteverdifaktoren N*?

Skatteverdifaktoren viser nåverdien av netto skattebesparelse pr evigvarende gjeldskrone. Formelen er:

[N* = 1- (1-Sb) * (1-Se) / (1-Sk)]

I telleren ser vi hva eierne får årlig etter skatt, når bedriftens kontantstrøm før skatt beskattes av en selskapsskatt, før eierne betaler en dividendeskatt på det resterende (M&M forutsetter som vi husker at overskudd utbetales i sin helhet til eierne).

(b) Hva er skatteverdifaktoren N* under ett-leddsbeskatning?

Ett-leddsbeskatning betyr at vi lever i et univers hvor bare selskapet beskattes (altså ingen kreditorskatt eller dividendeskatt).
Når det bare er selskapsskatt blir Se og Sk lik null. Hvis vi løser formelen over, og setter inn de tallene:
N* = 1 – (1-Sb) * (1-0) / (1-0)
N* = 1 – (1-Sb)*1 / 1
N* = Sb

(c) Hva er optimal gjeldsgrad under ett-leddsbeskatning? Bruk maks. tre linjer på svaret.

I oppgave 2 e) regnet vi på verdien av to bedrifter i et univers med ett-leddsbeskatning. Da kom vi frem til at bedriften med gjeld var mer verdt enn bedriften uten gjeld. Vi konkluderte med at dette var fordi renteskattebesparelsen førte til en høyere forventet kontantstrøm, som derfor førte til en høyere selskapsverdi. Vi kan konkludere med at denne skattebesparelsen vil bli høyere for hver egenkapitalkrone vi erstatter med en gjeldskrone. Enhver gjeldspolicy som maksimerer markedsverdien er best for eierne. Derfor blir optimal gjeldsgrad for et selskap i et univers med ett-leddsbeskatning: så høy som mulig.

(d) Hva er skatteverdifaktoren N* under nøytral to-leddsbeskatning?

N* kan innta tre former:
– >0 (gjeldsfavoriserende – altså at selskapsverdien øker med økt gjeldsgrad)
– <0 (egenkapitalfavoriserende – altså at selskapsverdien synker med økt gjeldsgrad)
– = 0 (nøytral – altså at selskapsverdien er uavhengig av finansieringen

I en nøytral to-leddsbeskatning er altså N* = 0

(e) Hva betyr nøytral to-leddsbeskatning for selskapsverdien?

Som nevnt over, nøytral to-leddsbeskatning vil si at selskapsverdien er uavhengig av hvordan selskapet er finansiert.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Oppgave 5

Konsulentselskapet Pelican ASA har nettopp fått en ny 5-års kontrakt som forventes å gi følgende kontantstrøm etter skatt i de neste 5 årene, (tallene er i millioner kroner):

Tid	1	2	3	4	5
Kontantstrøm	100	110	150	170	180

Denne 5-års kontrakten (prosjektet) krever en investering på 500 millioner kroner. Pelican forventer å finansiere prosjektet med egenkapital og et serielån. Pelican betaler 5% rente på lånet. Målsatt gjeldsandel er 50%. Prosjektets investeringsbeta er anslått til 1.0, markedets risikopremie er 6% før skatt, og risikofri rente er 4%. Selskapet betaler 28% skatt. Anta at Modigliani & Millers ett-leddsbeskatning (M&M63) gjelder (sK=sE=0).

(a) Hva er nåverdien av prosjektet dersom det hadde vært 100% egenkapitalfinansiert?

Først finner vi kapitalkostnaden til egenkapitalen. Da bruker vi vår gode gamle formel:
[Ke = rf + (E(rm) – rf)*βe]
Med våre tall:
0,04 + 0,06*1 = 0,10 = 10%

Da kan vi regne ut nåverdien av investeringen ved å legge den inn på finanskalkulatoren, eller manuelt ved å neddiskontere slik:

-500 + 100/1,10 + 110/1,10^2+……..+180/1,10^5 = 22,39

(b) Hvilken verdi har finansieringen? Pelican beregner gjeldsandel og gjeldskapasitet ut fra bokførte verdier.

Verdien av finansieringen uttrykkes ved nåverdien av renteskattebesparelsen. Da må vi første finne denne. Da må vi finne ut hva selskapet betaler i rente i perioden:

Tid	0	1	2	3	4	5
Lån IB	0	250	200	150	100	50
Lån UB	250	200	150	100	50	0
Avdrag	0	50	50	50	50	50
Renter*1	0	12,5	10	7,5	5	2,5
Renteskattebesparelse*2	0	3,5	2,8	2,1	1,4	0,7

*1: Lån IB * rentesats
*2: Rente * skattesats

Da kan vi finne nåverdien av renteskattegevinsten ved å neddiskontere renteskattegevinsten med lånerenta vår.
NV = 3,5/1,05 + 2,8/1,05^2 + …… + 0,7/1,05^5 = 9,39
(c) Hva er prosjektets justerte nåverdi?

Justert nåverdi = investeringens nåverdi + nåverdi av renteskattebesparelsen
Justert nåverdi = 22,39 + 9,39 = 31,78

(d) Redegjør for prosjektets lønnsomhet basert på investeringen og finansieringen. Bruk maks. 5 linjer.

Nåverdien er positiv, ergo er investeringen lønnsom. Vi får positiv nåverdi av renteskattegevinsten, og en positiv justert nåverdi, så da er finansieringen lønnsom. Prosjektet bør iverksettes.
Oppgave 6

Selskapet Mio ASA har et overskudd per aksje på 10 kroner. Selskapet betaler dividende, og ønsker å ha et stabilt utdelingsforhold på 50%. Overskudd per aksje neste år er forventet å bli

14 kr. Selskapet ønsker en dividende vekst på 10%.

Selskaper velger selv hvorvidt de skal betale ut utbytte (dividende), og størrelsen på et eventuelt utbytte. Utbetaling av dividende vil medføre at man tar verdier (inkludert cash) ut av selskapet, som vil øke gjeldsandelen. I dette faget sier vi at dividendepolitikken skal ha en effekt på selskapets verdi. Man må spørre seg: vil dividendeutbetalingen øke eller redusere verdien av selskapet med hensyn på eierne?

Det finnes flere måter å betale ut dividende på. Det vanligste er kontantutbetaling, altså at man betaler ut cash til aksjonærene gjerne basert på antall aksjer du har. Dette kan betales ut regelmessig (f.eks kvartalsvis), eller ekstraordinært (f.eks. hvis man har fått en gevinst på salg, eller man generelt ønsker å redusere likviditeten i bedriften).

(a) Hva må justeringsfaktoren i Lintner-modellen bli?
Lintner-modellen sier at dividendepolitikken til et selskap har to parametre:
1) Målsatt utbetalingsforhold (dividende pr aksje / overskudd pr aksje).
2) Hvor fort dagens dividende tilpasses målet.

For å forklare litt nærmere. 1) er grei. Det betyr bare at utbetalingsforholdet viser hvor stor prosentandel av overskuddet som skal betales ut, men 2) er kanskje litt mer uklar. Bedriftene ønsker gjerne å sette et utbetalingsforhold som en del av en stabil dividendepolitikk. Dersom en bedrift ikke har stabil vekst, kan endringene i dividendeutbetalingene fra år til år bli veldig store dersom man utelukkende skal benytte dette utbetalingsforholdet til å avgjøre fordeling. Som jeg har skrevet ønsker bedrifter en stabil dividendepolitikk, og det Lintners modell gjør er å sørge for at dividendeutbetalingene blir mer stabile enn overskuddet. Ustabile dividendeutbetalinger er vanligvis ikke gunstig. Litt om hvorfor:

I følge signalteorien vil investorer tolke dividendeendringer som en endring i forventet inntjening. Endring i forventet inntjening fører som vi vet til endring i selskapets verdi. Usikkerhet er noe av det verste markedet vet (bortsett fra de som trader derivater, da verdien på derivater øker med økt usikkerhet), og ettersom dividendeendring er en så kraftig indikasjon for investorene på fremtidig inntjening vil en ustabil dividendepolitikk føre til mye usikkerhet rundt selskapets verdi, som er ugunstig. Det finnes mye empiri som viser at markante endringer i dividendeutbetalinger fører til markante endringer i selskapets verdi. Det finnes imidlertid ikke noe empirisk bevis på at endring i dividende fører til endring i den fremtidige inntjeningen. Imidlertid er det vist en sterk kobling mellom årets dividendeutbetaling og fjorårets og årets overskudd, som egentlig bare betyr at dividendeendring et signal på fremtidig inntjening, men historisk inntjening (i år og i fjor).

Jesus, vi må komme tilbake til oppgaven. Jeg håper tanken bak Lintners modell virker mer fornuftig nå. Jeg kan gjenta det viktigste: bedrifter ønsker en stabil dividendepolitikk, og det Lintners modell gjør er å sørge for at dividendeutbetalingene blir mer stabile enn overskuddet.

Formelen vi bruker er:
DPAt = DPA(t-1) + a*[(b*OPAt)-DPA(t-1)
hvor:
DPA = Dividende pr aksje
OPA = Overskudd pr aksje
a = justeringsfaktor
b = målsatt utbetalingsforhold

Med våre tall (DPAt blir 5*1,10 fordi det er dividende pr aksje i år t, ettersom vi har en dividendevekst på 10%):

5*1,10 = 5 + a*[(0,50*14)-5)]
5,5 = 5 + a*(2)
2a = 0,5
a = 0,25

Justeringsleddet vi fant her vil påvirke hvor stor dividendeendringen skal være sammenlignet med endring i overskudd. Dersom a = 1 er prosentvis endring i dividendeutbetaling lik prosentvis endring i overskudd Som vi nevnte er det gjerne gunstig om dividendeendring er mer stabil enn endring i overskudd.

(b) Hva sier Irrelevansprinsippet om dividendepolitikken?

Bedriften må hele tiden ha en kontantstrømbalanse: Tilgang på penger = bruk av penger:
Kontantstrøm fra drift + ny gjeld + nytegnet egenkapital = renter + avdrag + nyinvestering + dividende

Dette kan kanskje være litt komplisert forklart i boken, og kanskje ikke veldig intuitivt, men prøv å les litt om det i boka.

(c) Hvorfor ønsker selskapet Mio ASA en dividendevekst?

Som vi har snakket om vil en dividendevekst tolkes av investorne som et signal på økt forventet inntjening i fremtiden fra selskapets styre og ledelse. Signalteorien sier så vakkert at dividenden er budbringeren, og budskapet er økt evne og vilje til å betale dividende i fremtiden

Posted on 17.09.201619.04.2022

Finansiell styring – Test 1

Som dere kanskje har lagt merke til på It´s Learning er det blitt lagt ut en test til faget finansiell styring. Jeg har løst det, og tenkte å dele det her for de som vil sjekke svarene sine, står fast eller bare vil skjønne mer om hvorfor det blir som det blir.

Oppgave 1

Et selskap skal opprettes med en startkapital på 6 millioner kroner. Ledelsen vurderer å finansiere selskapet ved hjelp av 120 000 aksjer til kurs 30 kroner pluss gjeld til 5 % rente. Ledelsen regner med at selskapet vil få et driftsresultat før renter på 360 000 kroner med sannsynlighet på 1/3 og på 900 000 kroner med sannsynlighet på 2/3. Se bort fra skatt.

a) Hva er det forventede overskuddet per aksje?

1/3 sannsynlighet for driftsresultat før renter på 360.000
2/3 sannsynlighet for driftsresultat før renter på 900.000

Forventet OFR (Overskudd Før Renter):
E(OPR) = (360.000*1/3) + (900.000*2/3) = 120.000 + 600.000 = 720.000

Lånebeløpet må være differansen mellom startkapitalen på 6.000.000 og den egenkapital som blir innskutt gjennom utstedelse av aksjer.
Lånebeløp = 6.000.000 – (120.000*30) = 2.400.000

Rente:
2.400.000*0,05 = 120.000

Forventet OER (Overskudd Etter Renter)
[OFR – renter]
720.000 – 120.000 = 600.000

Forventet OPA (overskudd pr aksje):
[OER/antall aksjer]
600.000/120.000 = 5 kroner

b) Hva er standardavviket til forventet overskudd pr. aksje?

Standardavviket er kvadratrota til variansen:
Sannsynligheten er 1/3 for et OPA på (360.000-120.000)/120.000 = 2
Sannsynligheten er 2/3 for et OPA på (900.000-120.000)/120.000 = 6,5

Her ser du at du kunne funnet forventet OPA ved å ta
(1/3*2) + (2/3*6,5) = 5

Varians:
1/3*(2-5)^2 + 2/3*(6,5-5)^2
= 3 + 1,5
= 4,5

Standardavviket er kvadratrota av 4,5, altså 2,12

c) Hva er det som måles med standardavviket til forventet overskudd per aksje? Bruk maks. 3 linjer på svaret.

Standardavviket er en måte å måle spredningen i fordelingen over mulige avkastninger i et prosjekt/investering. Standardavviket til forventet OPA er derfor en måte å måle usikkerheten (risikoen) til eierne på.

Ledelsen bestemmer seg for å finansiere selskapet med bare egenkapital.

d) Hvor mange aksjer må selskapet utstede til kurs 30 kroner per aksje?

Hvor mange aksjer må selskapet utstede til kurs 30 kroner for å få dekket kapitalbehovet på 6.000.000 kroner?

30*X=6.000.000
X= 200.000 aksjer

e) Hva er det forventede overskuddet per aksje når selskapet er 100% egenkapitalfinansiert?

Vi kan se to åpenbare konsekvenser av at selskapet velger å finansiere selskapet med bare egenkapital:

1. Antall aksjer stiger (som vil påvirke resultatet per aksje negativt, ettersom vi får et større tall i nevner)
2. Rentene bortfaller (som vil påvirke resultatet per aksje positivt, ettersom vi får et større tall i teller)

Forventet OFR har vi allerede regnet ut
(360.000*1/3) + (900.000*2/3) = 120.000 + 600.000 = 720.000

Ettersom vi ikke har noe renter, blir jo dette det endelige overskuddet. Vi deler dette på det nye antallet aksjer.
Da får vi OPA = 720.000/200.000 = 3,6

f) Vil standardavviket til forventet overskudd per aksje ved 100% egenkapitalfinansiering bli større eller mindre enn standardavviket til forventet overskudd per aksje i spørsmål b)? Begrunn svaret.
Bruk maks. 5 linjer på svaret. (Du trenger ikke å regne.)

Dersom det finnes investeringsrisiko, det vil si at det er mer enn 1 mulig utfall for OFR (slik som i denne oppgaven) vil en positiv gjeldsgrad påføre eierne finansieringsrisiko. Risikoen i forventet overskudd per aksje øker med gjeldsgraden. Ettersom standardavvik er et mål på risiko, og et høyere standardavvik betyr høyere risiko, vil standardavviket til forventet overskudd per aksje ved 0% gjeld (100% EK) være mindre enn standardavviket til forventet OPA ved mer enn 0% gjeld. Vi ser at forventet OPA er 5 kroner når vi har gjeld, og bare 3,6 uten gjeld. I sum over tid sier vi at en høyere risiko skal kompenseres med en høyere avkastning, og vise versa. Vi ser dette også ved å sammenligne utfallsrommet i oppgave e) med det i oppgave b). som Utfallsrommet i e) er 4.50-1.80=2.70. Utfallsrommet i b) er: 6.50-2.00=4.50 – altså større.

Oppgave 2

Noran ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 28 millioner kroner årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 14 %, risikofri rente er 3 %, og forventet risikopremie er 6 %. Noran opptar nå gjeld for 100 millioner kroner til markedsrente på 5 %. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad (gjeld/egenkapital) regnet til markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og se bort fra skatt.

a) Hvordan påvirkes selskapets totalkapitalkostnad av refinansieringen?

Jeg tenkte å si hva som menes med “M&M-forutsetningene”:

Forutsetningen for perfekt kapitalmarked innebærer følgende:
– Alle investorer har full informasjon om mulighetene i markedet.
– Alle kan låne til samme rente og med samme risiko, og det er ingen transaksjonskostnader.
– Egenkapitalen i selskapene er fritt omsettelig (aksjer og obligasjoner)
Miller og Modigliani (M&M) tar videre flere forutsetninger enn det som ligger i definisjonen av det perfekte kapitalmarked for å kunne finne verdien av selskaper innenfor samme risikoklasse. De forutsetter at for et gitt selskap vil sannsynlighetsfordelingen til overskudd før renter (OFR) være den samme i alle perioder. Videre antas OFR evigvarende og gjeldsgrad konstant over tid. Miller og Modigliani antar også at overskuddet i sin helhet betales ut som utbytte til eierne. Forventningsverdien til OFR og kontantstrømmen til kreditorer og til eiere blir derfor som uendelige annuiteter å regne.

Basert på disse forutsetningene kan vi si at:
Kapitalkostnaden til totalkapitalen = E(OFR)/V
hvor:
*E(OFR) er forventet overskudd før renter
*V er markedsverdien av selskapet (altså EK + gjeld)

Vi har fått oppgitt at egenkapitalkostnaden til selskapet før refinansieringen er 14%. Ettersom totalkapitalen utelukkende besto av egenkapital før refinansieringen, betyr det at totalkapitalkostnaden også var 14%. Dette er samme logikk som med totalkapitalrentabilitet og egenkapitalrentabilitet. Dersom man står overfor en bedrift som er 100% finansiert av egenkapital (ingen gjeld), vil totalkapitalrentabiliteten og egenkapitalrentabiliteten være like stor.

Dette kan vi kontrollregne, selv om det ikke er nødvendig:
[Kapitalkostnaden til totalkapitalen = E(OFR)/V]
Forventet OFR er jo 28 millioner. V, altså verdien av selskapet må være 200 millioner. Dette vet vi fordi selskapet har tatt opp et lån på 100 millioner, hvilket gir dem en G/E=1. Det betyr at ettersom G er 100 millioner, må også E være 100 millioner. V=totalkapitalen, altså G+E som må være 200 millioner.
Det gir oss:
28.000.000/200.000.000 = 0,14 etter refinansiering (og som vi så tidligere, vil ikke denne avhenge av finansieringen, så derfor er den 14% både før og etter refinansieringen.)

Oppsummert: Ettersom totalkapitalkostnaden er uavhengig av gjeldsgraden (med andre ord at finansieringsstrukturen ikke påvirker selskapets verdi) under disse forutsetningene, vil den forbli uendret etter refinansieringen.

b) Hva blir egenkapitalkostnaden etter refinansieringen?

I motsetning til totalkapitalkostnaden som er uavhengig av gjeldsgrad (G/E) er egenkapitalkostnaden økende ved økt gjeldsgrad. Dette skjønner vi når vi ser formelen for egenkapitalkostnad i M&Ms resultat nummer to:
Ke = Kt + (Kt – Kg)*G/E
Vi har allerede stadfestet at standardavviket, og derfor risikoen for eierne, øker når gjeldsgraden stiger. Uttrykket over viser hvordan dette påvirker egenkapitalkostnaden.

Så til oppgaven rent regneteknisk:

Da kan vi videre bruke flere formler. F.eks denne:
Ke = Kt + (Kt-Kg)*G/E
Ke = 0,14 + (0,14-0,05)*1
Ke = 0,23 = 23%

c) Kan du ved hjelp av en figur illustrere sammenhengen mellom totalkapitalkostnad og gjeldsgrad, og sammenhengen mellom egenkapitalkostnad og gjeldsgrad?

Ja, for dere kan jeg vel gjøre hva som helst:

Overstående figur gjelder altså for M&M sitt “univers” – uten skatt.
d) Hva er verdien av Noran når selskapet er 100% egenkapitalfinansiert?

Dette finner vi ved å ta overskuddet og dele på egenkapitalkostnaden (som for øvrig er lik totalkapitalkostnaden):

Markedsverdien av selskapet = V = 28.000.000/0,14 = 200.000.000

e) Hva er verdien av Noran etter at selskapet opptar gjeld?

Markedsverdien av selskapet = V = EK + G = 100.000.000 + 100.000.000 = 200.000.000

Oppgave 3
(OBS: Dette har vi ikke gått gjennom i forelesning enda – iallfall ikke på campus Trondheim.)

Callamare ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 28 millioner kroner årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 14 %, risikofri rente er 3 %, og forventet risikopremie er 6 %. Callamare opptar nå gjeld for 100 millioner kroner til markedsrente på 5 %. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad (gjeld/egenkapital) regnet til markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og at selskapet betaler 27% selskapsskatt. (Se bort fra investor-skatt, sE=sK=0).

a) Hva blir egenkapitalkostnaden etter refinansieringen?

Dette er et relativt greit uttrykk. Egenkapitalkostnaden er en funksjon av kapitalkostnaden for gjeld (Kg), kapitalkostnaden for et selskap finansiert med 100% egenkapital (Ku), bedriftsskatten (Sb) og gjeldsgraden (G/E):

Ke = Ku + (Ku – Kg)*G/E*(1-Sb)
Med våre tall:
Ke = 0,14 + (0,14-0,05)*1*(1-0,27) = 0,2057 = 20,57%

b) Hva blir totalkapitalkostnad av refinansieringen?

Her må vi finne vektet gjennomsnitlig kaptialkostnad (WACC – Weighted Average Cost of Capital), og justere den for skatt. Det er ikke noe vanskeligere enn å bruke den formelen vi kjenner fra tidligere kurs, og justere for skatt.
Vi ganger kapitalkostnaden for egenkapital og gjeld med vektingen av henholdsvis egenkapital og gjeld (altså andelen. I vårt tilfelle 50% av hver)
Altså, generelt:
Kt = (Ke*We) + (Kg*Wg)*(1-Sb)
Med våre tall:
Kt = (0,2057*0,5)+(0,05*0,5)*(1-0,27) = 0,1211 =12,11%

c) Hva er verdien av Callamare når selskapet er 100% egenkapitalfinansiert?

Minner om at vi fortsatt forholder oss til Miller og Modiglianis forutsetninger.
Kontantstrømmen forutsettes evigvarende, og som evige annuiteter flest kan man beregne selskapsverdien ved å neddiskontere årlig forventet kontantstrøm med avkastningskravet for et gjeldfritt selskap (Ku). Vi må justere den årlige forventede kontantstrømmen (E(OFRS)) for skatt ved å legge til skatteleddet.
Altså, generelt:
Vu = (E(OFRS)*(1-Sb)) / Ku
Med våre tall:
Vu = (28.000.000*(1-0,27)) / 0,14 = 146.000.000

d) Hva er verdien av Callamare etter at selskapet opptar gjeld?

Den generelle formelen er:
Vm = Vu + PG*N*
Hvor:
–Vm er altså er verdien av selskapet når det er delvis gjeldsfinansiert
–Vu er verdien av et 100% egenkapitalfinansiert selskap
–PG er pålydende gjeld
–PG * N* (PG ganget med N* – altså Nstjerne. Litt forvirrende ettersom jeg bruker stjerne som gangetegn også). PG*Nstjerne er verdien av renteskattfordelen ved gjeld.

N* defineres som:
[1-(1-Sb)*(1-Se)] / (1-Sk)
Som vi ser i oppgaveteksten at vi har ettleddsbeskatning, altså skal vi se bort fra investorskatt, hvilket betyr at Se og Sk = 0. Da ser vi at uttrykket blir:
1 – (1-Sb) * (1-0) / (1-0) —> = 1- (1-Sb) / 1 —–> = Sb

Da kan vi se at formelen Vm = Vu + PG*N* blir:
Vm = Vu + PG*Sb
Med våre tall:
146.000.000 + 100.000.000*0,27 = 173.000.000

Det innføres nå investor-skatt, sE=sK=27%.

e) Hva er nå verdien av Callamare etter at selskapet opptar gjeld?

Nå har vi fått investorskatt. Investorskatten er imidlertid lik selskapsskatten, så den som har gransket uttrykket for N* vil se at dette ikke vil gjøre mye forskjell på verdien av selskapet. Vi skal likevel regne det på vanlig måte. Kanskje lærer vi noe 😀

Formelen blir fremdeles lik den i oppgave d)
Vm = Vu + PG*N* – bare at nå er i utgangspunktet ikke N* lengre lik Sb, men vi må regne ut uttrykke, slik at vi får:
Vm = Vu + PG*[1-(1-Sb)*(1-Se) / (1-Sk)
Med våre tall:
Vm = 146.000.000 + 100.000.000*[1 – ((1-0,27)*(1-0,27)) / (1-0,27)]
Vm = 146.000.000 + 100.000.000*0,27 = 173.000.000

Som du kanskje ser ble N* lik Sb likevel, ettersom investorskatt og selskapsskatt i oppgaven er like.

Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:

Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen

Oppgave 4

Cansas ASA har en gjeldsgrad på 0,5. Selskapets investeringsbeta er 1,1, mens aksjebetaen er 1,5. Risikofri rente er 4%, og forventet avkastning på markedsporteføljen er 10%. Se bort fra skatt.

a) Hva er den systematiske risiko for selskapets gjeld?

Denne formelen husker vi fra tidligere kurs:
βi = βe*We + βg*Wg
Med våre tall:
1,1 = 1,5*2/3 + βg*1/3
1,1 = 1 + 0,33βg
0,1 = 0,33βg
βg = 0,3

b) Hva er kapitalkostnaden til gjelden?

Uttrykket for kapitalkostnaden til gjelden er:
Kg = rf+βg * [E(Rm) – rf * S*)
hvor
– rf er risikofri lånerente
– βg systematisk risiko for gjelden
– E(Rm) er forventet markedsavkastning
– S* er skattefaktoren. Den uttrykkes som (1-Sk)/(1-Se) hvor Sk og Se er henholdvis skatt på renteinntekt og egenkapitalinntekt.

Med våre tall:
0,04+0,3*[0,10-0,04]=0,058 = 5,8%
c) Hva betyr det at gjelden har en beta-verdi som er større enn null? Bruk maks. 3 linjer på svaret.

Dersom gjelden har en betaverdi som er større enn null, betyr det at gjelden har risiko. Med en gjeldsbeta større enn null finnes det konkursrisiko. Dersom det er sjanse for konkurs, vil en del av investeringsrisikoen bli veltet over fra eierne til kreditorene. For å gå litt utover de tre linjene, vil dette føre til at effektiv lånerente må stige over risikofri rente for å kompensere for den investeringsrisikoen som kreditorene må bære.

Oppgave 5

Tre-års spotrente er i dag 4%, og fire-års spotrente er 5%.

a) Hva er terminrenten fra år tre til år fire, (3f4)?

Implisitte terminrenter bygger på obeserverte effektive nullkupong-statsobligasjonsrenter.

Under forventningshypotensen (samt likviditetspremieteorien og markedssegmenteringsteorien, men disse er ikke viet plass i dette kurset) vil 1f2 som vist på paint-tegningen over være et anslag på en ettårsrente neste år. Det vil med andre ord være r1 om ett år.

Den generelle formelen bygger på et geometrisk gjennomsnitt:

Dette uttrykket kan generaliseres, og det er litt lettere å huske til eksamen:

I vårt tilfelle, blir det slik (jeg tar hele utredningen, men legg merke til at vi kommer frem til det generelle uttrykket som står over til slutt):

Med våre tall:

[(1+0,005)^4 / (1+0,04)^3] – 1 = 0,0805 = 8,05%

b) Gi en kort beskrivelse av forventningsteorien. Bruk maks 5 linjer på svaret.

Jeg bruker litt mer enn 5 linjer.

Forventningsteorien bygger kort fortalt på at teminstrukturkurven formes etter investorenes tanker om fremtidens rentenivå. Terminstrukturen vil være stigende dersom man forventer at rentenivået i markedet vil øke, og motsatt dersom man forventer at den vil falle. Dersom du ser for deg at en investor har valget mellom å kjøpe en obligasjon med enten lang eller kort løpetid, og den effektive renten er den samme på de to verdipapirene. Da er det lett å forstå at investoren ikke ville kjøpt obligasjonen med lang løpetid dersom han eller hun forventer at renten skal øke. Da ville investoren kjøpt en obligasjon med kort løpetid, og heller reinvestert pengene ved forfall. Dersom renten imidlertid forventes å falle, ville investoren kjøpt den lange obligasjonen – ja faktisk kunne investoren vært interessert i å kjøpe en lang obligasjon med lavere effektiv rente enn den korte også, avhengig av hvor stort rentefall investoren forventer.

Vi antar at kapitalmarkedskonkurransen er så sterk at de implisitte terminrentene i dagens lange rente blir lik de forventede fremtidige ettårsrentene i markedet. Forventningsteorien sier altså at du skal kunne oppnå samme avkastning ved å kjøpe en 2-åring (obligasjon med 2 års løpetid) som ved å kjøpe en ettåring i dag, og en ny ettåring om ett år. Altså at en toåring skal ha samme verdi som to påfølgende ettåringer. Det betyr også at en 4-åring skal gi samme avkastning som om du kjøper en 3-åring i dag, og en ettåring om 3 år.

Oppgave 6

Atona ASA er 100 % egenkapitalfinansiert. Selskapet har 1 million utestående aksjer med en markedsverdi på $100 per aksje. Atona trenger $40 millioner til et nytt prosjekt og bestemmer seg for å hente ny egenkapital i markedet. Selskapet gjør en emisjon med forkjøpsrett for gamle aksjonærer. Emisjonskursen blir satt til $80 per aksje. Se bort fra skatt.

1. Hva er en emisjon?
En emisjon er en finansieringsform som selskaper benytter når de har behov for mer egenkapital. Dette gjøres ved at selskapet mot innskudd i penger utsteder nye aksjer til dem som allerede eier aksjer i selskapet og/eller til noen som ikke eier aksjer i selskapet fra før.

2. Hva er en tegningsrett?
En tegningsrett gir deg rett (men ikke plikt) til å tegne og få tildelt nye aksjer i en emisjon i selskapet til en bestemt i pris, og i et bestemt tidsrom (tegningsperioden). Tegningsretten har normalt en økonomisk verdi dersom tegningskursen er lavere enn aksjekursen i markedet. Tegningsretter som ikke benyttes eller selges er uten verdi. De bortfaller etter tegningsperioden uten kompensasjon til eierne. Med andre ord bør du selge tegningsretten din dersom du ikke tenker å bruke den, hvis ikke er det et rent tap for deg, da aksjekursen kommer til å synke, uten at du blir kompensert med fortjeneste ved salg av tegningsretten (eventuelt fortjeneste i form av rabatt på aksjen hvis du velger å tegne deg)

Et eksempel:

(http://e24.no/boers-og-finans/bw-offshore-limited/bw-offshore-henter-penger-langt-under-dagens-kurs/23723858)

I sommerferien fikk jeg beskjed om en fortrinnsrettsemisjon i selskapet jeg har aksjer i; BW Offshore Limited, en av verdens ledende tilbydere innen utleie og drift av enheter for offshore, flytende produksjon og lagring. Selskapet er notert på Oslo Børs. Som mange har fått med seg er kanskje ikke offshore stedet hvor man ønsker å ha alle sparepengene sine plassert for tiden, men man trenger da litt spenning i hverdagen. Det er enorme restruktureringer innen olje og offshore for tiden. Styret i BWO hadde, som en del av en overordnet refinansiering av selskapet, vedtatt å gjennomføre en garantert fortrinnsrettet emisjon på inntil 856 millioner kroner, ved å utstede hele 8.599.810.000 nye aksjer til en tegningskurs på 0,10 øre per nye aksje.

Som aksjonær i BWO ble jeg tildelt tegningsretter. Disse tegningsrettene ga meg rett til å tegne meg for aksjer i fortrinnsrettsemisjonen. Jeg fikk tildelt ca 12,49 tegningsretter for hver aksje jeg hadde i selskapet. Hver tegningsrett ga meg rett til å kjøpe én ny aksje. Med andre ord fikk jeg mulighet til å kjøpe 12,49 nye aksjer til 0,10 kroner for hver aksje jeg hadde. Jeg kunne tegnet meg for flere enn det, men jeg hadde ikke vært garantert å fått dem. Dette ville avhenge av hvor mange som eventuelt ikke benyttet seg av sine tegningsretter.

Tegningsrettene poppet opp i nettbanken i nettbanken min hos Nordnet, som jeg bruker til å handle verdipapirer. Da hadde jeg valget om enten å bruke tegningsrettene til å tegne meg for nye aksjer, eller selge dem på samme måte som jeg ville solgt en “vanlig aksje”. Disse tegningsrettene ble omsatt for omtrent 5 øre. Det betyr at hvis jeg hadde tegnet meg hadde min kostnad pr aksje (hvis vi ser bort fra kurtasje) vært 15 øre pr aksje (10 øre i emisjonskurs og 5 øre i alternativkostnad ved ikke å selge dem). Aksjekursen i dag er på 27 øre, så det var mulighet for noe kortsiktig gevinst på akkurat disse aksjene. Uten at jeg skal spekulere i kursbevegelsene: den justerte aksjekursen i starten av tegningsperioden var på så lite som 0,14 øre, som kanskje kan forklare hvorfor noen valgte å selge sine tegningsretter?

Sånn i utgangspunktet så denne emisjonen veldig attraktiv ut for meg som aksjonær. Hva jeg valgte å gjøre med tegningsrettene får være en hemmelighet.

La oss ta en titt på oppgavene.

a) Hva blir ex-rights-kursen?

De trenger 40.000.000 til det nye prosjektet, og setter emisjonskursen til 80. Da må de utstede: 40.000.000/80=500.000 nye aksjer

Ex-rights-kursen er altså den kursen aksjen forventes å få i markedet etter at emisjonen er gjennomført. Formelen for den teoretiske ex-rights-kursen er:

Px = [(n*P0) + (m*Pe)] / (n+m)
hvor:
–n er antall gamle aksjer
–m er antall nye aksjer
–P0 er kursen før emisjonen (rights-on)
–Pe er emisjonskursen

Med våre tall:

(1.000.0000*100) + (500.000*80) / (1.000.0000 + 500.000)
= 93,33

b) Hva er verdien av en tegningsrett?

Verdien av tegningsretten:
Tn = (Px-Pe)*1/N
hvor
–Px er ex-rights-kursen
–N = n/m, altså gamle aksjer delt på nye aksjer.

Med våre tall:
N = n/m = 1.000.000/500.000 = 2

(93,33-80)* 1/2
=6,67

c) Anna Berg eier 20 aksjer i Atona før emisjonen, hvor mange tegningsretter får hun tildelt?

Dette spørsmålet har ikke et entydig svar. I pensumboka står det at “antall tegningsretter tilsvarer antall utestående aksjer. En investor med 50 aksjer i et selskap får derfor 50 tegningsretter ved enhver nyemisjon i selskapet”. Dette er jo åpenbart ikke helt riktig i et hvert tilfelle, jfr det jeg skrev om emisjonen i BW Offshore, hvor jeg fikk utstedt 12,49 tegningsretter per aksje jeg hadde. Dette ville imidlertid ha tilsvart at jeg hadde fått én tegningsrett per aksje, og at hver tegningsrett hadde gitt meg muligheten til å kjøpe 12,49 aksjer. Jeg har sendt en mail til foreleseren min for å få klarhet i dette, og svar hvorfor boka og foilene i kurset er så bastant. Det viktigste er at tegningsrettene du får gir deg mulighet til å opprettholde din relative (prosentvise) eierandel i selskapet.

Med andre ord, skal vi følge fagansvarlig sin tilnærming, vil Anna Berg få 20 tegningsretter. Ettersom forholdet mellom gamle og nye aksjer = 500.000/1.000.000 = 0,5 får hun bare kjøpt en halv aksje pr. tegningsrett. Hun får altså kjøpt 10 nye aksjer med sine 20 tegningsretter.

Alternativt, dersom selskapet ville utstede tegningsretter som ga et tegningsforhold 1:1 hadde selskapet måtte gitt Anna 20*0,5 = 10 tegningsretter, da forholdet mellom gamle og nye aksjer er 0,5 nye aksjer pr gamle.

d) Hvilket beløp må Anna Berg investere hvis hun deltar i emisjonen og benytter alle sine tegningsretter?

Anna kan kjøpe 10 nye aksjer. Emisjonskursen er 80 dollar per aksje. Altså må hun investere 800 dollar.

e) Hvor stor andel av Atona eier Anna Berg etter emisjonen?

Eierandelen er:
20+10 / 1.000.000 + 500.000 = 30/1.500.000 = 0.00002

Anna eier 0,002% av Atona.

Det er ikke en del av oppgaven, men:
Hva var eierandelen hennes før emisjonen?

20/1.000.000 = 0.00002 = 0,002%. Ergo, hun har gjennom å benytte seg av tegningsrettene sine opprettholdt sin eierandel etter emisjonen.

Håper dere lærte noe. Rop ut hvis dere finner noe feil, eller ønsker å diskutere det som står skrevet.