Her er løsningsforslag med utregninger og forklaringer på flervalgseksamen fra høst 2011. Når jeg refererer til “situasjon X” mener jeg situasjonene jeg har sammenfattet i dette innlegget: http://hobbyokonomen.blogg.no/1480082961_finansiell_styring__g.html
1. Albatros er 100% egenkapitalfinansiert. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalkostnaden er 12%. Se bort fra skatt.
Hva er Albatros? aksjebeta?
(a) 2,67
(b) 2,00
(c) 1,14
(d) 1,00
Bedriften er 100% finansiert av egenkapital, som betyr at egenkapitalkostnad og totalkapitalkostnad er det samme. Vi husker denne sammenhengen:
Totalkapitalkostnad = risikofri rente + risikopremie * beta
0,12 = 0,04 + 0,07*X
0,07X = 0,08
X = 1,14
2. Albatros er 100% egenkapitalfinansiert. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalkostnaden er 12%. Albatros har forventet overskudd for renter og skatt på 1 MNOK årlig i all fremtid, første gang om ett år. Selskapet har konstant kapasitet. Se bort fra skatt.
Hva er verdien av Albatros?
(a) 1.000.000 NOK
(b) 8.333.333 NOK
(c) 10.000.000 NOK
(d) 12.333.333 NOK
Her er vi i situasjon A: Uten skatt, uten gjeld
V = (OFRS) / Kt
V = 1.000.000/0,12 = 8.333.333
3. Hardwood er finansiert med 70% egenkapital og 30% risikofri gjeld. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalen har en beta på 1.14. Se bort fra skatt.
Hva er Hardwoods totalkapitalkostnad i følge Modigliani & Miller?s teori?
(a) 9,6%
(b) 12,0%
(c) 13,8%
(d) 15,4%
Her er vi i situasjon B: Uten skatt, med gjeld
Ke = Rf + [E(Rm) – Rf)*Beta
Ke = 0,04 + 0,07*1,14 = 0,12
Kt = (We*Ke)+(Wg*Kg)
Kt = 0,7*0,12 + 0,3*0,04
Kt = 9,6%
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
4. Hardwood er finansiert med 70% egenkapital og 30% risikofri gjeld. Risikofri rente er 4%, markedets risikopremie er 7%, og egenkapitalen har en beta på 1.14. Se bort fra skatt.
Hva er Hardwoods egenkapitalkostnad i følge Modigliani & Miller?s teori?
(a) 9,6%
(b) 12,0%
(c) 13,8%
(d) 15,4%
Egenkapitalkostnaden vil vanligvis øke med økt gjeldsgrad, (pga større risiko for eierne). Nå er det imidlertid sånn i denne oppgaven at det er risikofri gjeld, så det vil ikke påvirke egenkapitalkostnaden. Den vil være 12% slik som i oppgave 3, men vi kan regne den for syns skyld:
Ke = Ku + (Ku-Kg)*G/EK
Ke = 0,096 + (0,096-0,04)*3/7
Ke = 12%
5. Et selskap mottar et lån på 10 MNOK til 8% rente fra lokale myndigheter for å foreta en investering i lokalmiljøet. Et tilsvarende lån i finansmarkedet ville hatt en rente på 10%. Lånet er et serielån over 4 år, med etterskuddsbetaling av renter. Se bort fra skatt.
Hva er nåverdien av det subsidierte lånet?
(a) 0,20 MNOK
(b) 0,42 MNOK
(c) 0,76 MNOK
(d) 1,29 MNOK
Her må du sette opp en kontantstrøm for lånet, og neddiskontere det med r=10%
| (tall i 1000 kroner) | 0 | 1 | 2 | 3 | 4 |
| Opptak/avdrag | +10.000 | -2.500 | -2.500 | -2.500 | -2.500 |
| UB lån | 7.500 | 5.000 | 2.500 | 0 | |
| Renter (8%) | -800 | -600 | -400 | -200 | |
| Kontantstrøm | +10.000 | -3.300 | -3.100 | -2.900 | -2.700 |
Legg inn i finanskalkulatoren eller regne nåverdien manuelt, og du vil finne at NV = 415.000
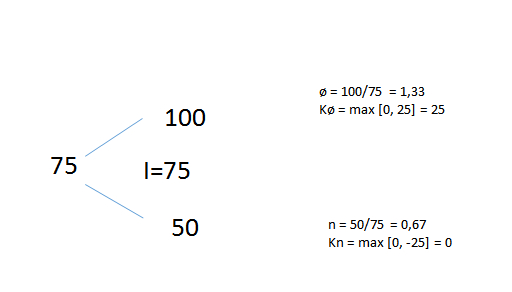
6. Markedsprisen på en aksje er 75 kroner. Om ett år vil markedsprisen være enten 50 eller 100 kroner. Investor kan låne til risikofri rente på 5% for den aktuelle perioden. En kjøpsopsjon på aksjen med ett år til forfall har en innløsningskurs på 75 kroner.
Hvilken verdi har kjøpsopsjonen i dag?
(a) 0 NOK
(b) 12,90 NOK
(c) 13,69 NOK
(d) 15,97 NOK
K0 = 1/1,05 * 25*[(1,05 – 0,667)/(1,33-0,667)
K0 = 13,75 (runder til nærmeste alternativ, 13,69)
7. Markedsprisen på en aksje er 75 kroner. Om ett år vil markedsprisen være enten 50 eller 100 kroner. Investor kan låne til risikofri rente på 5% for den aktuelle perioden. En salgsopsjon på aksjen med ett år til forfall har en innløsningskurs på 75 kroner.
Hvilken verdi har salgsopsjonen i dag?
(a) 7,77 NOK
(b) 8,89 NOK
(c) 10,12 NOK
(d) 12,37 NOK
Tar utgangspunkt i salg-kjøp paritet
K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf
S0 = 13,69 – 75 + 75/1,05 = 10,12
8. Fra regnskapene til selskapene Thecno og Elnor har du følgende informasjon:
| Thecno | Elnor | |
| Eiendeler | 400 | 500 |
| Egenkapital | 400 | 250 |
| Gjeld | 0 | 250 |
| E(OFRS) | 40 | 40 |
| E(OFS) | 40 | 30 |
Selskapene betaler ikke skatt.
I følge Modigliani & Miller’s teori er markedsverdien av Thecno og Elnor i likevekt den samme, den er beregnet til 475 MNOK.
Hva er egenkapitalkostnaden i Thecno og Elnor i likevekt?
(a) 8,00% and 10,00%
(b) 8,42% and 10,57%
(c) 8,42% and 13,33%
(d) 10,00% and 10,00%
Thecno er i situasjon A. Uten skatt, uten gjeld
V = 475
Kt = Ke = E(OFRS)/V
Kt = Ke = 40/475 = 8,42%
Elnor er i situasjon B: Uten skatt, med gjeld
V = 475
G = 250,
EK = 475-250 = 225
Eiers kontantstrøm etter at rentene er betalt er 30
Ke = KS(eier) / EK
Ke = 30 / 225
Ke = 13,33%
9. NewTech har akkurat bestemt å investere 40 MNOK i et miljøvennlig prosjekt. Ved bruk av ny teknologi, vil NewTech produsere oppvaskmaskiner som har et rengjøringssystem som bruker luft istedenfor vann. Den forventede kontantstrømmen fra prosjektet er 10 MNOK pr år i 5 år. Prosjektet finansieres med 50% egenkapital og 50% gjeld. Gjelden er et serielån på 5 år med 7% rente. Selskapet betaler 28% skatt, all investorer betaler også 28% skatt. Risikofri rente er 6%, den forventede avkastningen på markedsporteføljen er 13%. Prosjektets investeringsbeta er 1.2.
Hva er nåverdien av denne investeringen hvis vi forutsetter at prosjektet er 100% egenkapitalfinansiert?
(a) – 7,2 MNOK
(b) – 6,0 MNOK
(c) 5,2 MNOK
(d) 10,0 MNOK
Her er vi i situasjon E: med toleddsskatt, uten gjeld:
Kt = Rf + [E(Rm) – Rf]*Beta
Kt = 0,06 + [0,13 – 0,06)*1,2
Kt = 14,4%
NV = -40 + 10/1,144 + …. + 10/1,144^5
NV = -6,0
10. NewTech har akkurat bestemt å investere 40 MNOK i et miljøvennlig prosjekt. Ved bruk av ny teknologi, vil NewTech produsere oppvaskmaskiner som har et rengjøringssystem som bruker luft istedenfor vann. Den forventede kontantstrømmen fra prosjektet er 10 MNOK pr år i 5 år. Prosjektet finansieres med 50% egenkapital og 50% gjeld. Gjelden er et serielån på 5 år med 7% rente. Selskapet betaler 28% skatt, all investorer betaler også 28% skatt. Risikofri rente er 6%, den forventede avkastningen på markedsporteføljen er 13%. Prosjektets investeringsbeta er 1.2.
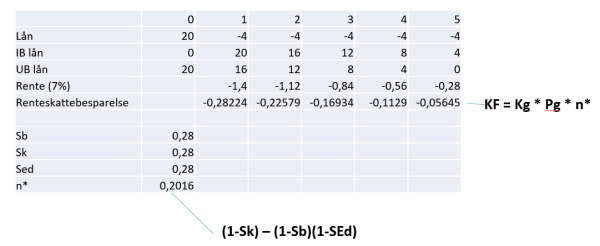
Hva er verdien av renteskattegevinsten?
(a) 0,76 MNOK
(b) 1,05 MNOK
(c) 1,80 MNOK
(d) 2,45 MNOK
Her må vi sette opp en kontantstrøm igjen:
OBS: Jeg ser at renteskattebesparelsen har fått negativt fortegn. Det skal være positive tall.
Vi legger “kontantstrømmen” av renteskattebesparelsen inn i finanskalkulator med diskonteringsrente etter skatt: 0,07*(1-0,28) = 5,04%
Da får vi NV av renteskattebesparelse = 0,7562
11. NewTech har akkurat bestemt å investere 40 MNOK i et miljøvennlig prosjekt. Ved bruk av ny teknologi, vil NewTech produsere oppvaskmaskiner som har et rengjøringssystem som bruker luft istedenfor vann. Den forventede kontantstrømmen fra prosjektet er 10 MNOK pr år i 5 år. Prosjektet finansieres med 50% egenkapital og 50% gjeld. Gjelden er et serielån på 5 år med 7% rente. Selskapet betaler 28% skatt, all investorer betaler også 28% skatt. Risikofri rente er 6%, den forventede avkastningen på markedsporteføljen er 13%. Prosjektets investeringsbeta er 1.2.
Hva er dette miljøvennlige prosjektets justerte nåverdi?
(a) -6,76 MNOK
(b) -5,24 MNOK
(c) 5,24 MNOK
(d) 6,76 MNOK
Justert nåverdi = nåverdien av investeringen + nåverdien av finansieringen
Vi har regnet ut at nåverdien av investeringen er -6,0 (oppgave 9) og at nåverdien av finansieringen er 0,7562
Justert nåverdi = -6+0,7562 = -5,24
12. Et selskap har 3 millioner utestående aksjer. Aksjeprisen er 20 kroner pr aksje. Selskapet har en gjeld på 40 MNOK. Selskapet betaler obligasjonseierne 6% rente. Aksjene i selskapet har en beta på 1,41. Risikofri rente er 4% og markedets risikopremie er 9,5%. Selskapet betaler 28% skatt.
Hva er selskapets gjennomsnittlige kapitalkostnad (WACC)?
(a) 11,63%
(b) 12,17%
(c) 12,84%
(d) 17,40%
Bedriften er finansiert på følgende måte:
Gjeld: 40 millioner
EK: 20*3 millioner = 60 millioner
Totalkapital = 100 millioner
WACC = Ke*We + Kg*Wg*(1-Sb)
Da må vi først finne Ke
Ke = Rf + [E(Rm) – Rf]*Beta
Ke = 0,04+0,095*1,41
Ke = 17,4%
WACC = 0,174*0,6 + 0,06*0,4*(1-0,28)
WACC = 12,17%
13. Amerikanske dollar noteres i Paris til 0,7293 og i Oslo til 5,7000. Euro noteres i Oslo til 7,72000.
Hvilken mulig arbitrasjegevinst kan du oppnå hvis du har 1 millioner kroner å investere?
(a) 12.398 kroner
(b) 13.546 kroner
(c) 59.977 kroner
(d) 70.000 kroner
Okey, så:
Dollar:
Paris: EUR/USD = 0,7293
Oslo: NOK/USD = 5,70
Euro:
Oslo: NOK/EUR = 7,7200
Det gir oss en krysskurs: EUR/USD*NOK/EUR = NOK/USD = 0,7293*7,72 = 5,6302
Vi ser at dollaren er “for dyr” i Norge:
1. Kjøper Euro i Norge for 1 million til kurs 7,72: 1.000.000/7,72 = 129.534 Euro.
2. Veksler disse EUR 129.534 til USD i Paris: 129.534/0,7293 = 177.614 Dollar.
3. Vi selger USD 177.614 i Norge: 177.614*5,70 = 1.012.398
Arbitrasjegevinst: 1.012.398 – 1.000.000 = 12.398
14. Du har eksportert varer til USA og skal motta et beløp i dollar om 6 måneder. For å redusere effekten av en mulig lav dollarkurs ønsker du å benytte en valutaopsjon.
Hvilken opsjonskontrakt er det mest fornuftig å bruke?
(a) Kjøp av en dollar salgsopsjon.
(b) Kjøp av en dollar kjøpsopsjon.
(c) Salg av en dollar salgsopsjon.
(d) Salg av en dollar kjøpsopsjon.
Du ønsker å sikre deg mot en lav kurs når du skal motta dollar. Da må du kjøpe en salgsopsjon, som gir deg rett til å selge dollaren du mottar.
15. En valutatunnel består av to opsjoner med forskjellige innløsningskurser. Anta at du har solgt en kjøpsopsjon med innløsningskurs 6 (kroner pr. utenlandsk valutaenhet) og kjøpt en salgsopsjon med innløsningskurs 4, begge med forfallsdato om 3 måneder. Du skal motta 1 million i den utenlandske valutaen om 3 måneder.
Hva blir den totale kontantstrømmen du mottar hvis dagskursen om 3 måneder er henholdsvis 3, 5 og 7?
(a) 1, 0 og 0 kroner.
(b) 3, 5 og 7 kroner.
(c) 4, 5 og 6 kroner.
(d) 7, 5 og 4 kroner
Jeg skal prøve å forklare dette veldig, veldig enkelt uten å bruke figurer. Iallfall er det slik jeg tolker oppgaven:
-Du har solgt en kjøpsopsjon, som forplikter deg til å selge til 6 dersom innehaveren ønsker å kjøpe til den kursen.
-Du har kjøpt en salgsopsjon, som gir deg rett men ikke plikt til å selge for 4 dersom du ønsker det. Utstederen er forpliktet til å kjøpe.
Dersom dagskursen er 3 får du den utenlandske valutaen, og ønsker å selge til 4 fordi 4 er høyere enn dagskursen. KS: 4
Dersom dagskursen er 5, ønsker du ikke å benytte deg av salgsopsjonen, fordi du får solgt den for 5 i markedet. KS: 5
Dersom dagskursen er 7 vil du sannsynligvis måtte innfri forpliktelsene dine til innehaveren av kjøpsopsjonen. Du får valutaen og selger den for 6. KS: 6
16. Alpha er 100% egenkapitalfinansiert. Forventet avkastning på aksjene er 10%. Selskapet planlegger å låne penger og deretter kjøpe tilbake aksjer slik at gjeldsgraden (gjeld/egenkapital) blir lik 1,00. Med en gjeldsgrad på 1,00 vil lånekostnaden være 5%. Det er ingen skatter.
Hva er forventet avkastning på egenkapitalen etter tilbakekjøpet?
(a) 10,00%
(b) 13,25%
(c) 15,00%
(d) 17,75%
Vi er i univers A og går over i univers B.
I univers A: uten skatt, uten gjeld er Kt og Ke lik, og vi får oppgitt at avkastningen på aksjene = 0,10.
Ke = Kt = 0,10
I univers B er gjeldsgraden 1 (Gjeld/EK = 1). Det betyr at det er like mye gjeld som egenkapital, altså 50/50.
I univers B finner vi Ke slik:
[Ke = Kt + (Kt – Kg)*G/EK[
Ke = 0,10 + (0,10-0,05)*1 = 15%
17. Arrow er 100% egenkapitalfinansiert og har en markedsverdi på 100 millioner dollar. Egenkapitalbetaen til selskapet er 0,50. Selskapets ledelse planlegger å endre kapitalstrukturen til selskapet ved å låne 40 millioner dollar (risikofri gjeld) og deretter bruke lånet samt 10 millioner dollar i kontanter for å kjøpe tilbake aksjer i selskapet.
Hva blir selskapets egenkapitalbeta etter tilbakekjøpet? Forutsett perfekte kapitalmarkeder.
(a) 0,50
(b) 0,75
(c) 0,90
(d) 1,00
Selskapet tilbakekjøper aksjer for 10 millioner. Dette reduserer antallet utestående aksjer i markedet. Tilbakekjøp av aksjer brukes ofte som en skatteeffektiv måte å overføre kontanter til aksjeeierne på, snarere enn å utbetale utbytte. I balansen føres tilbakekjøpte aksjer under egne aksjer i form av et negativt tall. Dette vil påvirke selskapsverdien, men ikke aksjeverdien. Hvorfor?
Se for deg at aksjeprisen i dette selskapet er 100 kroner og at det er 1 million utestående aksjer. Verdien til selskapet er da 100 millioner. Dersom selskapet tilbakekjøper aksjer for 10 millioner (altså 100.000 aksjer) vil verdien av egenkapitalen (selskapsverdien i et selskap uten gjeld) være 10 millioner mindre, altså 90 millioner.. Antall utestående aksjer vil være 100.000 færre, altså 900.000. Teoretisk aksjepris vil da være 90.000.000/900.000 = 100
Så til oppgaven:
I univers A: uten skatt, uten gjeld er beta til EK og beta til TK den samme: βt = βe = 0,5
Dersom de tar opp gjeld går de over i univers B: uten skatt, med gjeld.
Dette vil påvirke balansens høyreside:
Egenkapitalen vil reduseres fra 100 til 50 (100 – gjeld – tilbakekjøpte aksjer)
Gjeld vil øke fra 0 til 40
Sum EK + G = 90, som er den nye verdien til selskapet
Da finner vi βe:
[βe = βt + (βt – βg)*G/EK]
– Betaen til totalkapitalen vil ikke ha forandret seg.
– Betaen til gjeld er 0, da gjelden er risikofri (jfr. oppgaveteksten)
βe = 0,5+(0,5-0)*40/50
βe = 0,9
18. Hvilket av følgende utsagn er korrekt?
(a) Justert Nåverdi er bedre enn Egenkapitalmetoden og Totalkapitalmetoden dersom gjeldsgraden er konstant.
(b) Ved bruk av Justert Nåverdi diskonteres kontantstrøm ved 100% egenkapitalfinansiering etter skatt med egenkapitalkostnaden ved 100% egenkapital.
(c) Ved bruk av Egenkapitalmetoden diskonteres kontantstrøm til eiere etter skatt med egenkapitalkostnaden ved 100% egenkapital.
(d) Totalkapitalmetoden anvendes oftere enn Egenkapitalmetoden fordi det er enklere å beregne totalkapitalkostnaden enn egenkapitalkostnaden ved 100% egenkapital.
Justert nåverdi = nåverdien av investeringen + nåverdien av finansieringen
Dersom vi har en kontantstrøm på et prosjekt 100% finansiert av egenkapital, vil man bruke egenkapitalkostnaden (ved 100% EK) som diskonteringsrente.
19. Du tror at volatiliteten i aksjekursen vil være lavere enn implisitt volatilitet på opsjoner i aksjen.
Hvilken strategi vil du anbefale (innløsningskursen for opsjonene er lik dagens aksjekurs)?
(a) Selg en kjøpsopsjon og selg en salgsopsjon.
(b) Selg en kjøpsopsjon og kjøp en salgsopsjon.
(c) Kjøp en kjøpsopsjon og kjøp en salgsopsjon.
(d) Kjøp en kjøpsopsjon og selg en salgsopsjon.
Slik jeg har skrevet i et tidligere innlegg så har volatilitet (svingninger, standardavvik, risiko) innvirkning på derivatpriser. En opsjon er et derivat. Derivater blir mer verdt jo mer usikkerhet og jo større svingninger det er i det underliggende verdiobjektet. Det betyr at dersom du sitter på opsjoner, og du tror at den volatiliteten som er priset inn i den er større enn den reelle, så vil markedet snart fange opp dette og prisen på opsjonene vil falle. Du bør derfor selge alle opsjonene du har.
20. Bella har en gjeldsgrad (gjeld/egenkapital) lik 1,00 og en egenkapitalbeta på 1,50. Gjeldsbetaen er 0,30. Selskapsskattesatsen er 30%. Anta at Modligiani-Miller forutsetninger holder.
Hva er beta ved 100% egenkapitalfinansiering?
(a) 0,90
(b) 1,01
(c) 1,26
(d) 1,50
Vi er her i univers D: med ettleddsskatt, med gjeld.
Investeringsbetaen finner vi slik:
βI = βe*
βI = 1,01
21. Happy ASA har en egenkapitalkostnad på 10% ved 100% egenkapitalfinansiering. Selskapets lånekostnad er 7%. Selskapsskattesatsen er 30%, mens personbeskatning på inntekt fra egenkapital er 20%. Personbeskatning på renteinntekter utgjør 20%. Selskapets ledelse ønsker å undersøke virkningen av en mulig endring i kattesystemet. Noen politikere har foreslått å øke personbeskatningen på renteinntekt til 50% for å få et nøytralt skattesystem.
Hvilket av følgende utsagn er korrekt dersom det blir en slik fremtidig endring i skattesystemet?
(a) Selskapet vil ikke tjene på å ha mer gjeld dersom skattesystemet endres.
(b) Selskapet vil tjene på å ha mer gjeld dersom skattesystemet endres.
(c) Selskapet vil tjene på å ha mer gjeld med dagens skattesatser, men vil tjene på å ha mindre gjeld med de foreslåtte skattesatsene.
(d) Både (a) og (c).
Vi regner ut n* for de to scenarioene. n* viser som kjent netto skattefordel ved å erstatte en dividendekrone med en gjeldskrone.
n* = (1-Sk) – (1-Sb)*(1-Se)
n* i dag = (1-0,2) – (1-0,3)*(1-00,2) = 0,24
N* dersom endring = (1-0,5) – (1-0,3)*(1-0,2) = -0,04
Det vi ser er at n* blir negativ ved en endring, altså betyr det at det ikke vil være noen skattefordel ved å erstatte en dividendekrone med en gjeldskrone. I dag er den positiv, som betyr at selskapet får en økt skattefordel ved å oppta mer gjeld.
22. Et selskaps aksjekurs er 75 kroner i begynnelsen av året. Ved utgangen av året vil aksjekursen enten være 50 kroner eller 100 kroner. Investorer kan låne og plassere til risikofri rente på 5% for perioden. Både en salgs- og kjøpsopsjon på aksjen med ett år til forfall har innløsningskurs på 80 kroner. En investor har 100 aksjer i selskapet. Han ønsker å sikre seg mest mulig mot endringer i aksjekursen.
Hvilket av følgende utsagn er korrekt?
(a) Investoren kan sikre aksjeposisjonen ved å selge kjøpsopsjoner på 250 aksjer. Prisen for kjøpsopsjoner på 250 aksjer er 2.738 kroner.
(b) Investoren kan sikre aksjeposisjonen ved å selge kjøpsopsjoner på 250 aksjer. Prisen for kjøpsopsjoner på 250 aksjer er 1.750 kroner.
(c) Det er umulig å bruke salgsopsjoner for å sikre aksjeposisjonen.
(d) Investoren kan sikre aksjeposisjonen ved å kjøpe 167 salgsopsjoner. Kostnaden ved denne strategien er 1.750 kroner.
Eier 100 aksjer:
Sikringsforholdet (m):
[m = A0*(ø-n) / (Kø – Kn)]
m = 75*(1,33-0,67) / (20-0)
m = 2,5
Tolkningen av m:
– Vi må selge 2,5 kjøpsopsjoner pr eid aksje for å sikre oss.
K0 = 1 / 1,05 * [20*(1,05-0,67) / (1,33-0,67)]
K0 = 10,952524
100 eide aksjer, sikringsforhold 2,5 = 100*2,5 = 250 kjøpsopsjoner til pris 10,952524 – totalt: 2738
23. Agri Inc er tilbudt et 5-års lån på 100 millioner kroner med en årlig effektiv rente på null prosent (pålydende tilbakebetales på slutten av år 5). Effektiv markedsrente på tilsvarende lån er 10%. Det er ingen skatter.
Hva er nåverdien til lånet?
(a) 23,33 millioner kroner
(b) 26,54 millioner kroner
(c) 32,68 millioner kroner
(d) 37,91 millioner kroner
Her får vi en kontantstrøm som ser slik ut:
| 0 | … | 5 |
| 100 | -100 |
Vi må neddiskontere den til år 0 med den effektive markedsrenten på tilsvarende lån.
Nåverdien = +100 – 100/1,1^5
NV = 37,91
24. Et selskap har 3 millioner aksjer utestående med markedskurs 20 kroner/aksje og med en beta lik 1,4. Egenkapitalens bokverdi er 55 millioner kroner. Selskapet har i tillegg utstedt 50 millioner kroner i langsiktig gjeld, som for tiden omsettes til 80% av pålydende. Gjeldens effektive årlige avkastning før skatt er 10%. Risikofri rente er 6% og markedets risikopremie er 5%. Selskapet betaler 30% inntektsskatt.
Hva er selskapets veide gjennomsnittlige kapitalkostnad?
(a) 8,3%
(b) 10,1%
(c) 10,6%
(d) 11,8%
Veid gjennomsnittlig kapitalkostnad (Weighted Average Cost of Capital – WACC)
Selskapet har 3 millioner utestående aksjer med markedskurs 20 kroner. Da er egenkapitalen 20*3 millioner = 60 millioner.
Selskapets gjeld er 80% av 50 millioner (markedsverdi av gjeld), som er 40 millioner
Selskapets totalkapital er derfor 100 millioner.
Vekting av EK (We) blir 60/100=0,6
Vekting av gjeld (Wg) blir 0,4
WACC (Kt) = Ke*We + Kg*(1-s)*Wg
Finner Ke:
Ke = Rf + Risikopremie*beta
Ke = 0,06 + 0,05*1,4
Ke = 13%
Kt = 0,13*0,6 + 0,10*(1-0,3)*0,4 = 10,6%
25. Du vurderer en kjøpsopsjon (call) og en salgsopsjon (put) på samme underliggende aksje. Opsjonene har samme løpetid.
For at kjøps- og salgsopsjonens kurs skal utvikle seg i motsatt retning må:
(a) Prisen på den underliggende aksjen øke.
(b) Opsjonenes tid til forfall må øke.
(c) Volatiliteten til den underliggende aksjen må øke.
(d) Både opsjonenes tid til forfall og volatiliteten til den underliggende aksjen må øke.
Dersom prisen på den underliggende aksjen øker, så vil det føre til at salgsopsjonen (din rett til å selge aksjen til innløsningskurs) vil tape seg i verdi, fordi gevinsten din ved å kunne selge en aksje til innløsningskurs vil reduseres jo nærmere markedsprisen er innløsningskursen. Salgsopsjonen din har bare verdi dersom innløsningskursen er høyere enn markedskursen.
Tilsvarende vil din kjøpsopsjon styrke seg i verdi, fordi gevinsten din ved å kunne kjøpe en aksje til innløsningskurs vil øke jo høyere markedskursen er i forhold til innløsningskursen. Kjøpsopsjonen din har bare verdi dersom innløsningskursen er lavere enn markedskursen.
Opsjonens tid til forfall vil påvirke begge opsjonene i samme retning (økt verdi ved økt tid til forfall). Det samme gjelder volatilitet (økt verdi ved økt volatilitet).
26. Den risikofrie årsrenten er 6% i USA og 3% i eurosonen. Dagskursen er 1 EUR = 1,35 USD.
Hva er 12 måneders terminkurs mellom EUR og USD dersom arbitrasjegevinster ikke er mulig?
(a) 1 EUR = 1,3893 USD
(b) 1 EUR = 0,7198 USD
(c) 1 EUR = 1,3118 USD
(d) 1 EUR = 1,4739 USD
En terminkontrakt har mye til felles med opsjoner. Begge er finansielle instrumenter hvor verdien avhenger av et underliggende objekts verdi (et derivat). Begge instrumentene innebærer at to parter avtaler en fremtidig transaksjon, og at betingelsene for transaksjonen avtales i dag. Forskjellen er at både selger og kjøper (utsteder og innehaver) forplikter seg til å gjennomføre transaksjonen, mens vi husker at det for opsjoner er innehaveren som velger hvorvidt vedkommende ønsker å benytte seg av avtalen. Med mindre spotkurs ved innløsningstidspunktet er lik terminkursen, vil en av partene ha en gevinst på kontrakten, mens den andre parten vil ha en tilsvarende ugunst. Summen av gevinst og tap vil være null, og vi sier derfor at det er et “null-sum-spill”.
[Terminkurs = Spot * (1+rente i hjemlandet) / (1+rente i utlandet)]
Terminkurs = 1,35 * (1,06 / 1,03)
Terminkurs = 1,389
27. Dagskursen mellom enkelte valutaer er som følger:
1 EUR = 1,3500 USD, 1 EUR = 0,7050 GBP, 1 EUR = 0,9200 CHF.
Hva er dagskursen mellom amerikanske dollar og sveitsiske franc, samt mellom sveitsiske franc og britiske pund dersom det ikke foreligger noen arbitrasjemuligheter?
(a) 1 CHF = 1,2420 USD, 1 CHF = 0,6486 GBP
(b) 1 CHF = 0,6815 USD, 1 CHF = 1,3050 GBP
(c) 1 CHF = 0,8051 USD, 1 CHF = 1,5418 GBP
(d) 1 CHF = 1,4673 USD, 1 CHF = 0,7663 GBP
Så:
EUR/USD = 1,3500 (betaler 1,35 USD for en euro— 1,35 dollar gir én euro)
EUR/GBP = 0,7050
EUR/CHF = 0,9200 (betaler 0,9200 franc for en euro – 0,9200 franc gir én euro]
Vi vet vi betaler 0,9200 CHF for en EUR, som betyr at vi betaler 1/0,9200 = 1,0870 EUR for en CHF –> (CHF/EUR=1,0870)
CHF/USD = EUR/USD * CHF/EUR
1,35*1,0870 = 1,4673
Dersom det ikke foreligger arbitrasjemuligheter må en CHF koste 1,4673 USD
CHF/GBP = EUR/GBP * CHF/EUR
CHF/GBP = 0,7050*1,0870
CHF/GBP = 0,7663
Dersom det ikke foreligger arbitrasjemuligheter må en CHF koste 0,7663 GBP
Vanskelig å forstå? Enig. Det er kanskje ikke lett å se logikken, og det er lett at det kan gå i surr, men jeg skal forsøke å forklare hvordan jeg tenker.
Jeg skal finne ut hvor mange dollar jeg må betale for en sveitsisk franc (CHF/USD = dollar pr sveitsiske franc)
Da må jeg finne en krysskurs.
– EUR/USD forteller hvor mange dollar jeg må betale for en euro)
– CHF/EUR forteller hvor mange euro jeg betaler for en sveitsisk franc)
– Når jeg tar EUR/USD * CHF/EUR finner jeg en krysskurs. Du kan se for deg at du først veksler om fra dollar til euro til kurs 1,3500, så fra euro til sveitsiske franc til kurs 1,0870. Krysskursen viser derfor hva kursen må være for at du ikke skal få noen gevinst ved å veksle fra sveitsiske franc til dollar igjen.
Talleksempel:
#1: Du har 1 million dollar. Du veksler dem til euro: 1.000.000/1,35 = 740.740,741 euro.
#2: Du har nå 740.740,741 euro. Du veksler det til sveitsiske franc: 740.740,741/1,0870 = 681.454,224
#3.1: Du har nå 681.454,224 sveitsiske franc. Du vet du betaler 1,4673 dollar for 1 franc, det betyr at du betaler 1/1,4673 = 0,6815239 franc for en dollar. Du veksler franc til dollar: 681.454,224/0,6815239 = ca 1.000.000 dollar (litt avvik pga avrundende desimaler)
#3.2 Du kan også tenke slik: Du har nå 681.454,224 sveitsiske franc. Hva må kursen være for at du skal kunne veksle dette tilbake til 1.000.000 dollar?
1.000.000/681.454,224 = ca 1,4673
28. Laks AS har en gjeldsgrad (gjeld/egenkapital) på 0,8. Egenkapitalbetaen er 2,0, mens gjelden er risikofri. Selskapet oppnår hvert eneste år en kontantstrøm før skatt på enten 1.000.000 eller 500.000 med lik sannsynlighet. Risikofri rente er 3%, markedets risikopremie er 5% og selskapets skattesats er 20%.
Hva er totalverdien av Laks?
(a) 923.455
(b) 7.238.606
(c) 9.048.257
(d) 13.274.336
Her er vi i univers D: med ettleddsskatt, med gjeld.
Her har vi ikke oppgitt gjeld, EK eller totalkapital i kroner, men det trenger vi heller ikke. Vi må bare vite vektingen.
– Vi vet at gjeldsgraden er 0,8, altså at G/EK = 0,8.
– Det betyr at G/EK = 4/5. —> G= 4, EK = 5
– Da må G+EK være 4+5 = 9
– Da vet vi at vektingen av G = 4/9 og at vektingen av EK = 5/9
Vi vet at Ke = Rf + Risikopremie*beta
Ke = 0,03+0,05*2 = 13%
Kt = Ke*We + Kg*Wg(1-Sb)
Kt = 0,13*5/9 + 0,03*4/9*(1-0,2) = 8,29%
E(OFRS) = 1.000.000*0,5 + 500.000*0,5
E(OFRS) = 750.000
Eiernes kontantstrøm: 750.000*(1-0,2) = 600.000
Totalverdien av selskapet (V)
600.000/0,0829 =7.237.635,71
29. Hval ASA er et børsnotert selskap med en gjeldsgrad (gjeld/egenkapital) på 1. Det forventes at selskapet vil utbetale en dividende på kr 5 ved årets slutt (du er nå ved årets begynnelse), for deretter å øke med 2% årlig i overskuelig fremtid. Dagens aksjekurs i Hval er kr 25, og gjeldsbetaen er 0,5.
Krill AS er ikke børsnotert. Krill har en gjeldsgrad på 1,5 og forventes å utbetale en dividende på kr 10 per aksje ved årets slutt, men en etterfølgende årlig dividendevekst på 4%. Gjeldskostnaden i Krill er 5%.
Det er ingen skatt, risikofri rente er 1% og markedets risikopremie er 5%. Hval og Krill er i samme bransje med sammenlignbar eiendelsrisiko.
Hva er aksjekursen i Krill i likevekt?
(a) kr 45,45
(b) kr 49,08
(c) kr 55,56
(d) kr 114,29
Hval ASA har en gjeldsgrad på 1, som vil si at selskapet er finansiert med 50% EK og 50% gjeld.
Verdien pr. aksje (P0) kan estimeres ved å multiplisere første års forventede dividende (E(D1)), egenkapitalkostnaden (Ke) og vekst (v). Slik:
P0 = E(D1) / (Ke – v)
Vi kan nå bruke denne formelen til å finne Ke
25 = 5 / (Ke-0,02)
Ke = 22%
Da kan vi finne Kg:
Kg = risikofri rente + markedets risikopremie*gjeldsbeta
Kg = 0,01 + 0,05*0,5 = 3,5%
Da kan vi finne Kt. Grunnen til at vi vil det er at vi forutsetter at denne er den samme i Krill AS.
Kt = 0,22*0,5 + 0,035*0,5 = 0,1275
Nå kan vi bruke den samme formelen på Krill AS:
P0 = E(D1) / (Ke – v)
Vi må bare finne Ke først. Vi vet at gjeldsgrad = 1,5, som betyr at G/EK = 1,5. 3/2 =1,5. Da vet vi at G=3, EK=2, G+EK=5
Kt = Kg*Wg + Ke*We
0,1275 = 0,05*3/5 + Ke*2/5
Ke = 24,38%
P0 = E(D1) / (Ke – v)
P0 = 10 / (0,2438-0,04) = 49,068
30. Dagens aksjekurs i Alpha er kr 150. Om 12 måneder kan aksjekursen enten stige til kr 180 eller falle til kr 140. Prisen på en salgsopsjon (put) på aksjen i Alpha med innløsningskurs kr 160 og forfall om 12 måneder er kr 10,55.
Hva er 12-måneders risikofri rente?
(a) 3,50%
(b) 5,20%
(c) 8,60%
(d) 10,67%
Okey. Denne er ikke veldig hyggelig, men vi får sett på en del sammenhenger når vi løser den. La oss gå i gang.
Vi husker denne formelen fra en tidligere oppgave:
[m = A0*(ø-n) / (Kø – Kn)]
Denne brukte vi til å konkludere med hvor mange kjøpsopsjoner vi trengte pr. eid aksje for å sikre oss. Når vi skal bruke den på å regne hvor mange salgsopsjoner vi trenger for å sikre oss, må vi snu den (altså 1/m). Da blir den sånn:
m = (Kø-Kn) / A0*(ø-n)
m = 0-20 / 150*(1,2-0,9333)
m = -0,5
Vi kan bruke følgende sammenheng for å finne Rf:
I = Kn – A0*n*m / 1+Rf
I = 20 – (150*0,93*(-0,5)) / 1+Rf
I = 20 + 70 / 1+Rf
S0 = A0*m+I
10,55 = 150(-0,5) + I
I = 85,55
I = 20 + 70 / 1+Rf
85,55 = 20+70 / 1+Rf
Rf = 5,20%
Det var det eksamenssettet. Følg med for mer, og si gjerne fra hvis jeg har gjort noe feil 🙂


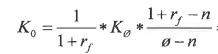
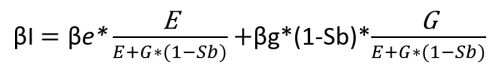
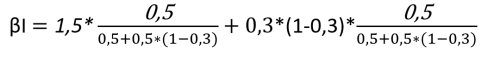
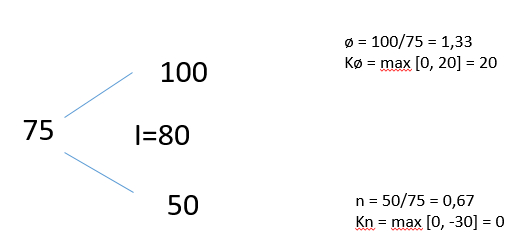


Kan du gi en rask beskrivelse av hva som skal legges inn i kalkulatoren på oppg. 10? Jeg ga opp å forstå det sist og fikk ikke til noen nåverdi-oppgaver. Leste en annen guide på nett, men alt går bare i null.
Marie:
Du bare legger inn kontantstrømmene, og “avkastningskrav” 5,04%
I oppg 20 er det oppgitt skatt og derfor har du tatt hensyn til skatten i beregningen av egenkapitalandel og gjeldsandel (under brøkstreken). I oppg 24 er det også oppgitt skatt i oppgavetekst, men du har ikke her tatt hensyn til skatten i beregning av gjeldsandel og egenkapitalandel (gange med 1-sb under brøkstreken). Hvorfor det?
Spm: Jeg tar hensyn til skatten ved å gange Kg med (1-Sb)
WACC (Kt) = Ke*We + Kg*(1-s)*Wg
Det er også viktig å merke seg at i oppgave 20 regner vi på beta, og i oppgave 24 regner vi på WACC. Forskjellige formler og sammenhenger.