Nå mine venner. Dette innlegget er way overdue, jeg vet. Jeg har hatt mye å gjøre med verv og ikke minst ferdigstillelse av strategioppgaven.
NOK UNNSKYLDNINGER, HÆ? La oss komme igang! Rop ut om noe er feil eller uklart.
OBS: Når jeg prater om “univers A, B, C” osv, refererer jeg til de ulike universene av skatt/gjeld. Du bør lese dette korte innlegget før du setter i gang:
Gjeldsfinansiering og verdi
Litt teori først. En opsjon er et derivat. Et derivat er et finansielt instrument hvor verdien av instrumentet avhenger av verdien et underliggende objekt – f.eks. en aksje. En opsjon gir eieren (innehaveren) av opsjonen en rett, men ikke en plikt, til å kjøpe (kjøpsopsjon) eller selge (salgsopsjon). Du har et valg: en “option”. Selgeren (utstederen) av opsjonen har derimot en plikt til å innfri opsjonen. Altså:
| Kjøper (innehaver) | Selger (utsteder) | |
| Kjøpsopsjon | Har rett, men ikke plikt, til å kjøpe | Har plikt til å selge |
| Salgsopsjon | Har rett, men ikke plikt, til å selge | Har plikt til å kjøpe |
Et eksempel. Du eier noen aksjer i Statoil. Statoil-aksjen i dag ligger på 132 kroner. Jeg utsteder en salgsopsjon som gir deg retten til å selge en Statoil-aksje til meg for 140 kroner om 3 måneder. Hvis aksjekursen forholder seg i ro, vil du etter 3 måneder kunne selge en aksje for 8 kroner over markedsverdi. Opsjonen er da lønnsom å bruke, og vi sier at den er “in the money”. Hvis prisen på Statoil-aksjen på den annen side stiger til 145 kroner, vil du tjene mer på å selge aksjene dine i markedet enn ved å benytte deg av salgsopsjonen. Ettersom du bare har en rett – men ikke en plikt – til å selge, kan du bare la være å benytte deg av opsjonen. Du har da bare tapt det du betalte for opsjonen i utgangspunktet. Opsjonen er ikke lønnsom å utøve, og vi sier at den er “out of the money”.
Oppgave 1
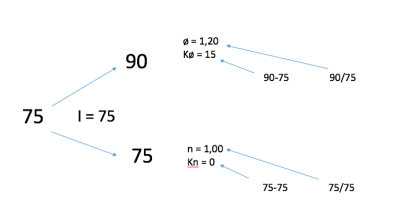
Aksjene i selskapet Aramas ASA omsettes i dag for 75 kroner per aksje. Det omsettes også kjøps- og salgsopsjoner på aksjene i Aramas med forfall om tre måneder og innløsningskurs på 75 kroner. Det forventes at markedsverdien av aksjen er enten 90 kroner eller 75 kroner om tre måneder. Risikofri rente er 4% per år.
(a) Hva er kjøpsopsjonens verdi i dag?
I eksemplet i teorigjennomgangen over er det lett å se at verdien av salgsopsjonen på innløsningstidspunktet er 140-132 = 8. Hva opsjonsverdien er 3 måneder frem i tid er ikke like lett å se. Legg merke til at risikofri rente er oppgitt pr. år å være 4%, så med andre ord 4/12 = 0,33% hver mnd, altså 1% pr kvartal.
K0 = 1/(1+0,01) * 15 * (1,01-1)/(1,20-1)
K0 = 0,9900990*15*0,05
K0 = 0,7425743
(b) Hva er salgsopsjonens verdi?
S0 = 0,7425743 – 75 + 75/1,01
S0 = 0
Dette svaret kommer vel kanskje ikke som noen bombe. Opsjonen gir deg muligheten til å selge en aksje for 75 kroner etter tre måneder. Aksjekursen vil enten være 75 eller 90, som betyr at du kan selge aksjen til nøyaktig samme pris (75) eller en betraktelig høyere pris (90) i markedet, som betyr at opsjonen ikke gir noen (mer)verdi, som betyr at opsjonsverdien er null. Hvis innløsningskursen er lik markedskurs sier vi at opsjonen er “at the money”.
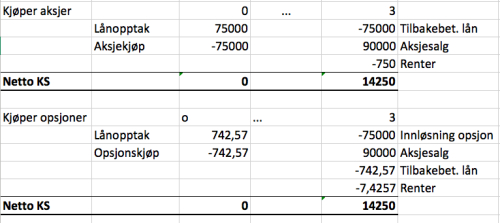
Du har stor tro på at markedet vil prise aksjene i Aramas ASA til 90 kroner om tre måneder, og bestemmer deg for å investere i selskapet. Du har ingen penger, men kan låne penger i banken til risikofri rente. Du kan enten låne penger til å kjøpe 1000 aksjer i dag eller låne penger og kjøpe 1000 kjøpsopsjoner i dag med innløsningskurs på 75 kroner.
(c) Vis kontantstrømmen for de to alternativene i dag og om 3 måneder.
Antar at lånerenter blir betalt samtidig som lånet blir tilbakebetalt, ettersom oppgaven ber oss om å vise kontantstrømmen i dag og om 3 måneder (og ikke for månedene mellom.) Antar at aksjene selges ved innløsningstidspunkt i alternativ 1. Antar også at i alternativ 2 skjer oppgjøret på en sånn måte at vi ikke trenger å ta opp nytt lån (f.eks. at du shorter aksjen, bruker pengene på å innløse opsjonen, og kjøper tilbake aksjene igjen samme dag (“intradag”), som ikke utløser renter/avgifter, eller at utsteder av opsjonen bare betaler deg mellomlegget mellom innløsningskursen og markedsverdien på aksjen).
(d) Hvilket alternativ velger du? Forklar hvorfor.
I utgangspunktet har de to alternativene identiske nettokontantstrømmer, og samme nåverdi. Ved å kjøpe aksjen og selge den etter tre måneder får du hele gevinsten fra verdiøkningen selv. Ved å kjøpe opsjoner vil noe av verdiøkningen “gå tapt” i form av premie til utsteder. I dette tilfellet blir mergevinsten fra alternativ 1 “spist opp” av den ekstra rentekostnaden. Noen aspekter å tenke på da er kanskje:
– Er det tilrådelig å låne 75.000 for å kjøpe aksjer?
– Høyere rente på alternativ 1 gir skattefordel mot alternativ 2.
– Risiko. Riktignok er det ingen risiko i denne oppgaven i så måte. Hvis aksjekursen forblir 75, vil du i alternativ 1 ha tapt de 750 kronene i renter. I alternativ to vil du ha tapt 742,57 kroner i opsjonspremie og 7,43 kroner i renter som også blir 750 kroner.
Hva ville jeg valgt? Jeg ville nok kjøpt aksjene, fordi det er mindre stress.
(e) Hva er det som avgjør kjøpsopsjonens verdi i tillegg til dagens aksjekurs?
– Volatilitet (svingninger, standardavvik) i aksjekursen øker verdien av opsjonen, fordi den gir mindre risiko enn en aksje som svinger mye.
– Tid til forfall. Jo lengre tid det er til forfall, jo større er sjansen for at opsjonen ved forfall er lønnsom å benytte seg av (“in the money”). Det gir også mening at en rett (uten plikt) er mer verdt jo lengre du har retten.
– Innløsningskurs. Verdien av kjøpsopsjoner avtar med økende innløsningskurs, fordi jo høyere innløsningskursen er, jo mindre er sannsynligheten for at aksjekursen ved forfall er høyere enn innløsningskursen.
– Risikofri rente. Jo høyere rente, jo lavere nåverdi av innløsningskursen.
Oppgave 2
To selskaper, Oljeutstyr ASA og Oil-Ex ASA, er helt like bortsett fra at Oljeutstyr er 100% egenkapitalfinansiert med en totalkapitalkostnad på 10%. Oil-Ex har en gjeldsgrad på 1. Oil-Ex har 5 millioner kroner i gjeld og en gjeldskostnad på 5%. Se bort fra skatt.
(a) Hva er egenkapitalkostnaden i de to selskapene?
I en bedrift som er 100% finansiert av egenkapitalen vil alltid totalkapitalkostnaden og egenkapitalkostnaden være den samme. Hvorfor? Fordi totalkapital er summen av egenkapital og gjeld, så hvis selskapet bare har egenkapital er totalkapitalen lik egenkapitalen.
Vi vet derfor at egenakpaitalkostnaden i Oljeutstyr = 10%
Vi vet også at totalkapitalkostnaden er uavhengig av gjeldsgraden, altså vet vi at ettersom de to selskapene er helt like bortsett fra måten de er finansiert på, er totalkapitalkostnaden i Oil-Ex ASA også 10%. Da kan vi bruke brekkstangformelen f.eks:
[Ke = Kt + (Kt – Kg)*G/EK]
Ke = 0,10 + (0,10-0,05)*1 = 0,15 = 15%
(b) Forklar hvorfor det er forskjell på egenkapitalkostnaden i de to selskapene.
I Oljeutstyr er hele selskapet finansiert av egenkapital. I Oil-Ex har imidlertid selskapet forpliktelser til sine långivere som skal ha sine renter og avdrag før eierne får det som eventuelt måtte bli til overs. Dette betyr at risikoen for eierne øker, som betyr at egenkapitalkostnaden også øker.
(c) Forventet overskudd før renter er 1 million kroner i begge selskapene, hva er verdien av egenkapitalen i de to selskapene?
Verdien av egenkapitalen finner vi ved å ta forventet overskudd etter renter og dele på egenkapitalkostnaden.
Oljeutstyr: [EK = E(OER)/Ke]—> 1.000.000 / 0,10 = 10.000.000
Oil-Ex: EK = (1.000.000-(5.000.000*0,05)) / 0,15 = 5.000.000
(d) Hva er totalverdien av de to selskapene?
I dette faget bruker vi en metode for verdsetting av selskaper som kalles “Enterprise Value” (EV)-metoden. Den baserer seg på at man ved oppkjøp ikke bare kjøper selskapets verdier, men også dens gjeld, penger og pengeekvivalenter. Selskapsverdien er beregnet som:
markedsverdi + gjeld – cash
Grunnen til at man trekker fra cash er at disse vil være tilgjengelig etter oppkjøpet for å betale ned gjeld eller lignende. Jeg tror ikke vi kommer til å få en oppgave på eksamen hvor man trenger å ta hensyn til cash, men jeg nevner det likevel. Markedsverdi (market cap) er som vi vet prisen pr aksje ganget med antall utestående aksjer.
For Oljeutstyr som ikke har noe gjeld blir EV = markedsverdi –> EV = EK –> EV=10.000.0000
For Oil-Ex som har gjeld blir EV = markedsverdi + gjeld –> 5.000.000 + 5.000.000 = 10.000.000
Forenklet kan vi se at verdien av et selskap ikke avhenger av finansieringen i et univers uten skatt.
Myndighetene bestemmer at Oljeutstyr ASA og Oil-Ex må betale 28 % selskapsskatt. Se bort fra investor- og kreditorskatt.
(e) Hva er totalverdien av Oljeutstyr og av Oil-Ex nå når de betaler skatt?
Oi, her har vi fått innført skatt. Det går bra. Vi må bare vite at:
#1: Skatten vil redusere forventet overskudd
#2: Skatten vil føre til en skattebesparelse på rentene våre (renteskattebesparelse)
Vi bruker følgende sammenhenger.:
Verdi for selskap uten gjeld = [E(OERS) / Ke]
Verdi for selskap med gjeld = Verdi for selskap med gjeld + Pålydende Gjeld * Skattesats –> [Vm = Vu + PG*Sb]
Med våre tall, og prøv å se effekten av skatten i de to selskapene. :
Oljeutstyr: Vu = 1.000.000*(1-0,28) / 0,10 = 7.200.000
Her ser vi at skatten fører til et lavere forventet overskudd.
Oil-Ex: Vm = 7.200.000+(5.000.000*0,28) = 8.600.000
Her ser vi at skatten først fører til et lavere forventet overskudd, men at vi på grunn av renteskattebesparelsen får en høyere forventet kontantstrøm, og derfor høyere selskapsverdi.
Oppgave 3
(a) Anta at vi har følgende markedskurser og rentesatser: (Alle rentene er perioderenter).
Spot NOK/USD: 8,00
Rentesats NOK plassering 6 mnd.: 2,10 %
Rentesats NOK lån 6 mnd.: 2,15 %
Rentesats USD plassering 6 mnd.: 1,00 %
Rentesats USD lån 6 mnd.: 1,20 %
I. Hva blir 6 måneders terminkurs for en norsk eksportør hvis det ikke er noen arbitrasjemulighet?
II. Hva blir 6 måneders terminkurs for en norsk importør hvis det ikke er noen arbitrasjemulighet?
En terminkontrakt har mye til felles med opsjoner. Begge er finansielle instrumenter hvor verdien avhenger av et underliggende objekts verdi (et derivat). Begge instrumentene innebærer at to parter avtaler en fremtidig transaksjon, og at betingelsene for transaksjonen avtales i dag. Forskjellen er at både selger og kjøper (utsteder og innehaver) forplikter seg til å gjennomføre transaksjonen, mens vi husker at det for opsjoner er innehaveren som velger hvorvidt vedkommende ønsker å benytte seg av avtalen. Med mindre spotkurs ved innløsningstidspunktet er lik terminkursen, vil en av partene ha en gevinst på kontrakten, mens den andre parten vil ha en tilsvarende ugunst. Summen av gevinst og tap vil være null, og vi sier derfor at det er et “null-sum-spill”.
Her bruker vi følgende sammenheng.
På I.: Terminkurs for eksportør = Spot * (1+plasseringsrente i hjemlandet) / (1+lånerente i utlandet)
På II: Terminkurs for importør = Spot * (1+lånrente i hjemlandet) / (1+plasseringsrente i utlandet)
Med våre tall:
I: 8*(1+0,021) / (1+0,012) = 8,07
II: 8* (1+0,0215) / (1+0,01) = 8,09
(b) En norsk importør har gjort en avtale om levering av et vareparti fra en tysk leverandør på 1 millioner euro med levering om 2 måneder og 1 måneds betalingsutsettelse. Importøren har mottatt følgende opplysninger fra sin bankforbindelse:
(Alle rentene er periode renter).
Spot NOK/EUR: 9,00
Termintillegg 3 måneder: 3,56 øre
3 måneders lånerente NOK: 1,20 %
3 måneders plasseringsrente EUR: 1,00 %
Kjøpsopsjoner EUR 3 måneder (innløsningskurs = terminkurs) har premie 1,5%.
Importøren vurderer å terminsikre den åpne posisjonen, eventuelt å benytte en valutaopsjon.
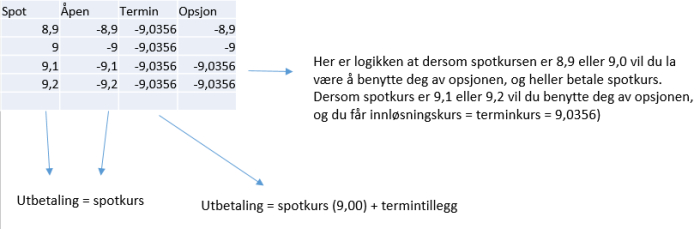
Spotkurs om 3 måneder blir:
8,9 eller 9,0 eller 9,1 eller 9,2
Alle med like stor sannsynlighet. Hva blir importørens kontantstrøm for de tre alternativene (åpen, termin, opsjon) om 3 måneder?
(Åpne bildet i ny fane dersom ikke hele teksten vises)
c) Hva er fordelene/ulempene med terminsikring fremfor bruk av opsjon?
En fordel er at man kan redusere risiko for valutasvingning. Som jeg nevnte avtales den valutakursen man skal benytte for den fremtidige transaksjonen allerede i dag, slik at risikoen for svingninger ikke påvirker noen av partene. En annen fordel er at man slipper å betale en premie for å inngå kontrakten, slik man må med opsjoner. Dette er en ren kostnad man betaler for fleksibiliteten en opsjon innebærer, men den slipper man å betale ved inngåelse av terminkontrakt. En vanlig opsjon er dessuten mye mer standardisert enn en terminkontrakt, som man kan tilpasse mer etter behov.
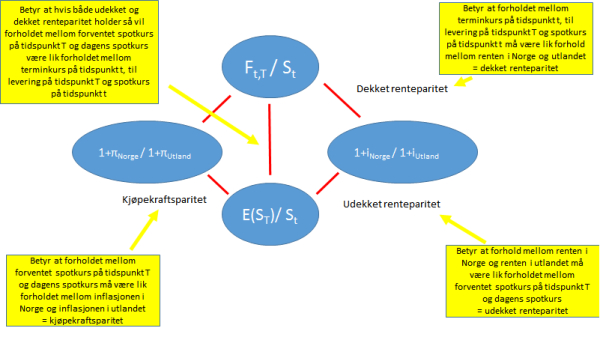
Jeg legger ved denne lille sammenhengen mellom paritetene, som noen kanskje har sett før, hvis den kan være til hjelp:
Oppgave 4
Selskapet Admiral ASA er finansiert med egenkapital og gjeld.
(a) Hva viser skatteverdifaktoren N*?
Skatteverdifaktoren viser nåverdien av netto skattebesparelse pr evigvarende gjeldskrone. Formelen er:
[N* = 1- (1-Sb) * (1-Se) / (1-Sk)]
I telleren ser vi hva eierne får årlig etter skatt, når bedriftens kontantstrøm før skatt beskattes av en selskapsskatt, før eierne betaler en dividendeskatt på det resterende (M&M forutsetter som vi husker at overskudd utbetales i sin helhet til eierne).
(b) Hva er skatteverdifaktoren N* under ett-leddsbeskatning?
Ett-leddsbeskatning betyr at vi lever i et univers hvor bare selskapet beskattes (altså ingen kreditorskatt eller dividendeskatt).
Når det bare er selskapsskatt blir Se og Sk lik null. Hvis vi løser formelen over, og setter inn de tallene:
N* = 1 – (1-Sb) * (1-0) / (1-0)
N* = 1 – (1-Sb)*1 / 1
N* = Sb
(c) Hva er optimal gjeldsgrad under ett-leddsbeskatning? Bruk maks. tre linjer på svaret.
I oppgave 2 e) regnet vi på verdien av to bedrifter i et univers med ett-leddsbeskatning. Da kom vi frem til at bedriften med gjeld var mer verdt enn bedriften uten gjeld. Vi konkluderte med at dette var fordi renteskattebesparelsen førte til en høyere forventet kontantstrøm, som derfor førte til en høyere selskapsverdi. Vi kan konkludere med at denne skattebesparelsen vil bli høyere for hver egenkapitalkrone vi erstatter med en gjeldskrone. Enhver gjeldspolicy som maksimerer markedsverdien er best for eierne. Derfor blir optimal gjeldsgrad for et selskap i et univers med ett-leddsbeskatning: så høy som mulig.
(d) Hva er skatteverdifaktoren N* under nøytral to-leddsbeskatning?
N* kan innta tre former:
– >0 (gjeldsfavoriserende – altså at selskapsverdien øker med økt gjeldsgrad)
– <0 (egenkapitalfavoriserende – altså at selskapsverdien synker med økt gjeldsgrad)
– = 0 (nøytral – altså at selskapsverdien er uavhengig av finansieringen
I en nøytral to-leddsbeskatning er altså N* = 0
(e) Hva betyr nøytral to-leddsbeskatning for selskapsverdien?
Som nevnt over, nøytral to-leddsbeskatning vil si at selskapsverdien er uavhengig av hvordan selskapet er finansiert.
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
Oppgave 5
Konsulentselskapet Pelican ASA har nettopp fått en ny 5-års kontrakt som forventes å gi følgende kontantstrøm etter skatt i de neste 5 årene, (tallene er i millioner kroner):
| Tid | 1 | 2 | 3 | 4 | 5 |
| Kontantstrøm | 100 | 110 | 150 | 170 | 180 |
Denne 5-års kontrakten (prosjektet) krever en investering på 500 millioner kroner. Pelican forventer å finansiere prosjektet med egenkapital og et serielån. Pelican betaler 5% rente på lånet. Målsatt gjeldsandel er 50%. Prosjektets investeringsbeta er anslått til 1.0, markedets risikopremie er 6% før skatt, og risikofri rente er 4%. Selskapet betaler 28% skatt. Anta at Modigliani & Millers ett-leddsbeskatning (M&M63) gjelder (sK=sE=0).
(a) Hva er nåverdien av prosjektet dersom det hadde vært 100% egenkapitalfinansiert?
Først finner vi kapitalkostnaden til egenkapitalen. Da bruker vi vår gode gamle formel:
[Ke = rf + (E(rm) – rf)*βe]
Med våre tall:
0,04 + 0,06*1 = 0,10 = 10%
Da kan vi regne ut nåverdien av investeringen ved å legge den inn på finanskalkulatoren, eller manuelt ved å neddiskontere slik:
-500 + 100/1,10 + 110/1,10^2+……..+180/1,10^5 = 22,39
(b) Hvilken verdi har finansieringen? Pelican beregner gjeldsandel og gjeldskapasitet ut fra bokførte verdier.
Verdien av finansieringen uttrykkes ved nåverdien av renteskattebesparelsen. Da må vi første finne denne. Da må vi finne ut hva selskapet betaler i rente i perioden:
| Tid | 0 | 1 | 2 | 3 | 4 | 5 |
| Lån IB | 0 | 250 | 200 | 150 | 100 | 50 |
| Lån UB | 250 | 200 | 150 | 100 | 50 | 0 |
| Avdrag | 0 | 50 | 50 | 50 | 50 | 50 |
| Renter*1 | 0 | 12,5 | 10 | 7,5 | 5 | 2,5 |
| Renteskattebesparelse*2 | 0 | 3,5 | 2,8 | 2,1 | 1,4 | 0,7 |
*1: Lån IB * rentesats
*2: Rente * skattesats
Da kan vi finne nåverdien av renteskattegevinsten ved å neddiskontere renteskattegevinsten med lånerenta vår.
NV = 3,5/1,05 + 2,8/1,05^2 + …… + 0,7/1,05^5 = 9,39
(c) Hva er prosjektets justerte nåverdi?
Justert nåverdi = investeringens nåverdi + nåverdi av renteskattebesparelsen
Justert nåverdi = 22,39 + 9,39 = 31,78
(d) Redegjør for prosjektets lønnsomhet basert på investeringen og finansieringen. Bruk maks. 5 linjer.
Nåverdien er positiv, ergo er investeringen lønnsom. Vi får positiv nåverdi av renteskattegevinsten, og en positiv justert nåverdi, så da er finansieringen lønnsom. Prosjektet bør iverksettes.
Oppgave 6
Selskapet Mio ASA har et overskudd per aksje på 10 kroner. Selskapet betaler dividende, og ønsker å ha et stabilt utdelingsforhold på 50%. Overskudd per aksje neste år er forventet å bli
14 kr. Selskapet ønsker en dividende vekst på 10%.
Selskaper velger selv hvorvidt de skal betale ut utbytte (dividende), og størrelsen på et eventuelt utbytte. Utbetaling av dividende vil medføre at man tar verdier (inkludert cash) ut av selskapet, som vil øke gjeldsandelen. I dette faget sier vi at dividendepolitikken skal ha en effekt på selskapets verdi. Man må spørre seg: vil dividendeutbetalingen øke eller redusere verdien av selskapet med hensyn på eierne?
Det finnes flere måter å betale ut dividende på. Det vanligste er kontantutbetaling, altså at man betaler ut cash til aksjonærene gjerne basert på antall aksjer du har. Dette kan betales ut regelmessig (f.eks kvartalsvis), eller ekstraordinært (f.eks. hvis man har fått en gevinst på salg, eller man generelt ønsker å redusere likviditeten i bedriften).
(a) Hva må justeringsfaktoren i Lintner-modellen bli?
Lintner-modellen sier at dividendepolitikken til et selskap har to parametre:
1) Målsatt utbetalingsforhold (dividende pr aksje / overskudd pr aksje).
2) Hvor fort dagens dividende tilpasses målet.
For å forklare litt nærmere. 1) er grei. Det betyr bare at utbetalingsforholdet viser hvor stor prosentandel av overskuddet som skal betales ut, men 2) er kanskje litt mer uklar. Bedriftene ønsker gjerne å sette et utbetalingsforhold som en del av en stabil dividendepolitikk. Dersom en bedrift ikke har stabil vekst, kan endringene i dividendeutbetalingene fra år til år bli veldig store dersom man utelukkende skal benytte dette utbetalingsforholdet til å avgjøre fordeling. Som jeg har skrevet ønsker bedrifter en stabil dividendepolitikk, og det Lintners modell gjør er å sørge for at dividendeutbetalingene blir mer stabile enn overskuddet. Ustabile dividendeutbetalinger er vanligvis ikke gunstig. Litt om hvorfor:
I følge signalteorien vil investorer tolke dividendeendringer som en endring i forventet inntjening. Endring i forventet inntjening fører som vi vet til endring i selskapets verdi. Usikkerhet er noe av det verste markedet vet (bortsett fra de som trader derivater, da verdien på derivater øker med økt usikkerhet), og ettersom dividendeendring er en så kraftig indikasjon for investorene på fremtidig inntjening vil en ustabil dividendepolitikk føre til mye usikkerhet rundt selskapets verdi, som er ugunstig. Det finnes mye empiri som viser at markante endringer i dividendeutbetalinger fører til markante endringer i selskapets verdi. Det finnes imidlertid ikke noe empirisk bevis på at endring i dividende fører til endring i den fremtidige inntjeningen. Imidlertid er det vist en sterk kobling mellom årets dividendeutbetaling og fjorårets og årets overskudd, som egentlig bare betyr at dividendeendring et signal på fremtidig inntjening, men historisk inntjening (i år og i fjor).
Jesus, vi må komme tilbake til oppgaven. Jeg håper tanken bak Lintners modell virker mer fornuftig nå. Jeg kan gjenta det viktigste: bedrifter ønsker en stabil dividendepolitikk, og det Lintners modell gjør er å sørge for at dividendeutbetalingene blir mer stabile enn overskuddet.
Formelen vi bruker er:
DPAt = DPA(t-1) + a*[(b*OPAt)-DPA(t-1)
hvor:
DPA = Dividende pr aksje
OPA = Overskudd pr aksje
a = justeringsfaktor
b = målsatt utbetalingsforhold
Formelen forteller oss at årets dividendeutbetaling = fjorårets utbetaling +/- noe. Justeringsleddet avhenger av hvor mye målsatt dividendeutbetaling (basert på utbetalingsforholdet og det faktiske overskuddet) avviker fra fjorårets utbetaling og hvor raskt bedriften ønsker at dividenden skal endres (hvor mye mer stabil dividenden skal være i forhold til overskuddet).
Med våre tall (DPAt blir 5*1,10 fordi det er dividende pr aksje i år t, ettersom vi har en dividendevekst på 10%):
5*1,10 = 5 + a*[(0,50*14)-5)]
5,5 = 5 + a*(2)
2a = 0,5
a = 0,25
Justeringsleddet vi fant her vil påvirke hvor stor dividendeendringen skal være sammenlignet med endring i overskudd. Dersom a = 1 er prosentvis endring i dividendeutbetaling lik prosentvis endring i overskudd Som vi nevnte er det gjerne gunstig om dividendeendring er mer stabil enn endring i overskudd.
(b) Hva sier Irrelevansprinsippet om dividendepolitikken?
Irrelevansprinsippet sier at under gitte forutsetninger vil det ikke være mulig å påvirke verdien av et selskap gjennom dividendepolitikk. Den påstår at det er et nullsumspill som gjør at effekten av dividendeendring vil nøytraliseres av en tilsvarende endring i aksjekurs. Forutsetningene er:
1) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
2) Egenkapitalbeskatningen er nøytral.
3) Alt annet enn dividendepolitikken holdes konstant (dividendepolitikken påvirker inne investerings- og gjeldsgradsbeslutninger).
Bedriften må hele tiden ha en kontantstrømbalanse: Tilgang på penger = bruk av penger:
Kontantstrøm fra drift + ny gjeld + nytegnet egenkapital = renter + avdrag + nyinvestering + dividende
Med de forutsetningene jeg listet opp, betyr ligninga over at enhver endring i dividende vil kreve en tilsvarende endring i nytegnet egenkapital (emisjoner). Forutsetningene i irrelevansprinsippet sier at dersom vi øker dividendeutbetalingene med X kroner, vil det samtidig måtte utstedes nye aksjer for å hente inn X kroner. Når vi fordeler makredsverdien på flere aksjer, blir verdien på aksjen vannet ut, og mindre verdt.
Dette kan kanskje være litt komplisert forklart i boken, og kanskje ikke veldig intuitivt, men prøv å les litt om det i boka.
(c) Hvorfor ønsker selskapet Mio ASA en dividendevekst?
Som vi har snakket om vil en dividendevekst tolkes av investorne som et signal på økt forventet inntjening i fremtiden fra selskapets styre og ledelse. Signalteorien sier så vakkert at dividenden er budbringeren, og budskapet er økt evne og vilje til å betale dividende i fremtiden

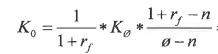
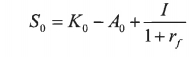

Hei,
Jeg ser på oppgave 5a, jeg skjønner ikke hvor du får “0,06” etter å ha brukt “Ke” formelen.
Skal det ikke bli ifølge formelen [Ke = rf + (E(rm) – rf)*βe]: 0,04 + (0,06-0,04)*1 ?? Hvor blir det av risikofri renten?
Bror: Hei. Klammen [(E(rm) – rf)] er markedets risikopremie. Den er allerede ferdig utregnet med andre ord.
Hei!
Hvis du ser på oppgave 3b i Høst 2015, så finner de at KØ = 10 kr, og KN = 0 ?
Hvordan kan den bli 0? Er det “fremtidig pris” – innløsningskurs?
helzot: Hei. Kø og Kn vil aldri være negative. Kø vil være det høyeste alternativet av 0 og ø*A0 – I). Kn vil være det høyeste alternativet av 0 og (n*A0 – I)
Vi sier:
Kø = max [0, ø*A0 – I]
Kn = max [0, n*A0 – I]
I oppgaven du refererer til er ø =1,25 (fordi 100 er 125% av 80)
Da blir Kø = max [0, 1,25*80 – 90] —> Kø = max [0, 10] —> Kø = 10
og Kn = max [0, 1*80 – 90] —-> Kn = max [0, -10] –> Kn = 0
Hei! Du gjør vel ikke tilfeldigvis case til økonometri i høst også? 🙂
Ja, så det er ø * A0 – I, men det vil være samme svar som å bare gjøre det slik du har gjort det?
Så uansett hva, når den blir negativ, så blir den egentlig 0?
Elisabeth: Du kan sende det til meg på mail, [email protected], så skal jeg se på det.
helzot: Stemmer.
I oppg. 1a ser jeg at for å finne n og Kn så har du brukt 75/75 og 75-75.
Men “hvilke” 75-summer er dette? Er det innløsningskurs delt på potensiell markedsverdi? Eller motsatt? 75 kr er brukt flere ganger, så jeg lurer på hva den ordrette formelen for å finne n og Kn er 🙂
Marie: Hei. Jeg forstår at jeg kanskje skulle skrevet det litt annerledes.
ø = den prosentvise prisøkningen fra A0 til At (altså innløsningstidspunkt). Så det er regnet ut ved At/A0
n er tilsvarende et forholdstall som viser hvor stor At er i forhold til A0. Også her er det At/A0
Kø = det høyeste av 0(null) og (A0*ø – I). A0*ø er jo i dette tilfellet 75*1,20 = 90, i I er innløsningskursen. Så den 75’en jeg har trukket fra er I-
Marie:
Kn blir (slik som Kø) det høyeste av 0 og A0*n – I. I dette tilfellet blir 75-75 også. Logikken er at denne verdien aldri kan bli mindre enn null, så hvis A0*n blir et negativt tall er Kn alltid null.
Så hvis jeg skal sette det opp litt mer forståelig – med ord, kan jeg si:
ø = høyeste markedsverdi / innløsningskurs
n = laveste markedsverdi / innløsningskurs
Kø = høyeste markedsverdi – innløsningskurs
Kn _ laveste markedsverdi – innløsningskurs
?
Marie: Nei. ø og n blir høyst/lavest markedsverdi ved innløsningstidspunkt delt på markedsverdi på tidspunkt A0.
Kø blir den høyeste summen av 0 og høyeste markedsverdi – innløsningskurs, og Kn blir den høyeste summen av 0 og laveste markedsverdi – innløsningskurs.
“I nevneren ser vi hva eierne får årlig etter skatt, når bedriftens kontantstrøm før skatt beskattes av en selskapsskatt, før eierne betaler en dividendeskatt på det resterende (M&M forutsetter som vi husker at overskudd utbetales i sin helhet til eierne)”
Mener du ikke i telleren? eller er det (1-Sk) du mener?
Oda: Jo! Har du sett. Endret! 🙂
Hei, kunne du ha forklart hvordan du kom frem til svarene i 1C? jeg har sittet med det lenge, men jeg skjønner ikke hvordan man skal regne det
Anonym: Hva er det du ikke får til? Det er et vanlig kontantstrømoppsett. Rentene er 3 måneders rente basert på rentesats og den gjelden du tar opp, som du betaler på tidspunkt 3.
Hvordan regner du rentene i 1C
Anonym: Du kan låne til 4% i året. 4% i året betyr 1% for 3 måneder. Da blir renten for et på på 75.000 lik 75.000*0,01 =750.
I 5b, hvor kommer delt på 1.05 fra? Og finnes det en snarvei for det på kalkulatoren?
Line: Dette er helt ordinær nåverdiberegning slik vi gjorde førsteåret… Du neddiskonterer med 1 + r. Ettersom r=5% blir 1+r lik 1,05. Dette gjør du naturligvis enkelt på kalkulatoren, hvis ikke kan det ta lang tid.