OBS: Når jeg prater om “univers A, B, C” osv, refererer jeg til de ulike universene av skatt/gjeld. Du bør lese dette korte innlegget før du setter i gang:
Gjeldsfinansiering og verdi
1. I en binomisk opsjonsmodell er kjøpsopsjonens verdi avhengig av:
(a) Dagens pris på den underliggende aksjen.
(b) Sannsynligheten for at den underliggende aksjen stiger eller synker.
(c) Volatiliteten til den underliggende aksjen.
(d) Både (a) og (c).
Dette påvirker kjøpsopsjonens verdi
– Prisen på det underliggende instrumentet (aksjen)
– Volatilitet (svingninger, standardavvik) i aksjekursen øker verdien av opsjonen, fordi den gir mindre risiko enn en aksje som svinger mye.
– Tid til forfall. Jo lengre tid det er til forfall, jo større er sjansen for at opsjonen ved forfall er lønnsom å benytte seg av (“in the money”). Det gir også mening at en rett (uten plikt) er mer verdt jo lengre du har retten.
– Innløsningskurs. Verdien av kjøpsopsjoner avtar med økende innløsningskurs, fordi jo høyere innløsningskursen er, jo mindre er sannsynligheten for at aksjekursen ved forfall er høyere enn innløsningskursen.
– Risikofri rente. Jo høyere rente, jo lavere nåverdi av innløsningskursen.
2. Hvordan kan du ved hjelp av en aksje, en kjøpsopsjon og en salgsopsjon oppnå en risikofri investering?
(a) Kjøp en aksje, selg en kjøpsopsjon, og kjøp en salgsopsjon.
(b) Kjøp en aksje, kjøp en kjøpsopsjon, og selg en salgsopsjon.
(c) Kjøp en aksje, selg en kjøpsopsjon, og selg en salgsopsjon.
(d) Selg en aksje, kjøp en kjøpsopsjon, og kjøp en salgsopsjon.
Bruker følgende sammenheng:
A + S = B + K
Hvor:
A = aksje
S = salgsopsjon
B = obligasjon (risikofri komponent)
K = kjøpsopsjon
B = A + S – K
3. Anta at skattesystemet favoriserer gjeld, det vil si at det ikke er nøytralisert av rentenivået, og at gjelden er risikofri uansett gjeldsgrad.
Hvilken av følgende påstander er korrekt dersom selskapet øker sin gjeldsgrad utover dagens nivå?
(a) Egenkapitalkostnaden øker og totalkapitalkostnaden synker.
(b) Gjeldskostnaden og totalkapitalkostnaden er begge konstante.
(c) Totalkapitalkostnaden stiger.
(d) Verdien av selskapet synker.
-Dersom skattesystemet er nøytralt vil Kt være uavhengig av gjeldsgrad
-Dersom skattesystemet favoriserer EK vil Kt være stigende med økt gjeldsgrad
-Dersom skattesystemet favoriserer gjeld vil Kt være synkende med økt gjeldsgrad
-Vi har flere ganger konkludert med at Ke er stigende med økt gjeldsgrad.
4. Hvilken eller hvilke av disse forutsetningene gjelder for dividende-irrelevansresultatet?
(a) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
(b) Egenkapitalbeskatningen er nøytral.
(c) Alt annet enn dividendepoltikken holdes konstant.
(d) Både (a), (b), og (c).
Irrelevansprinsippet sier at under gitte forutsetninger vil det ikke være mulig å påvirke verdien av et selskap gjennom dividendepolitikk. Den påstår at det er et nullsumspill som gjør at effekten av dividendeendring vil nøytraliseres av en tilsvarende endring i aksjekurs. Forutsetningene er:
1) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
2) Egenkapitalbeskatningen er nøytral.
3) Alt annet enn dividendepolitikken holdes konstant (dividendepolitikken påvirker inne investerings- og gjeldsgradsbeslutninger).
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
5. Et selskap har nylig utstedt en 10-års obligasjon med 6% kupongrente. Markedsrenten på tilsvarende obligasjoner er 4% i dag.
Obligasjonen omsettes i dag:
(a) Til pålydende.
(b) Over pålydende.
(c) Under pålydende
(d) Det er ikke nok informasjon til å besvare spørsmålet.
Kupongrente > markedets avkastningskrav –> pris > pålydende
Kupongrente < markedets avkastningskrav –> pris < pålydende
Kupongrente = markedets avkastningskrav –> pris = pålydende
6. Prisen på en aksje i Olives ASA dagen før retten til dividende bortfaller (siste rights-on dag) er $60. Dividenden er på $8 per aksje. Investorer betaler 28% skatt på kapitalgevinst og dividendeinntekt.
Hva er forventet pris på en aksje første ex-rights dag?
(a) $ 5,76
(b) $ 8,00
(c) $43,20
(d) $52,00
Aksjekursen vil synke tilsvarende dividende pr aksje, altså 8 dollar.
7. Markedsverdien på aksjene i Ruccula ASA er 100 kroner pr. aksje den 01.01.2012. Ruccula er 100% egenkapitalfinansiert. Selskapets aksjonærer har et avkastningskrav på 18% etter skatt. Ruccula betaler 28% selskapsskatt. Selskapet utbetaler ikke dividende i løpet av året.
Hva er forventet aksjekurs 31.12.2012?
(a) 85 kroner
(b) 113 kroner
(c) 118 kroner
(d) 151 kroner
Aksjonærenes avkastningskrav er 18% etter skatt. Aksjekursen blir 100*1,18 = 118 kroner.
8. Aksjekapitalen i Morningside ASA består av 4 millioner aksjer verdsatt til 50 kroner pr. aksje den 01.01.2012. Forventet overskudd neste år er 24 millioner kroner etter skatt. Morningside er 100% egenkapitalfinansiert. Selskapets aksjonærer har et avkastningskrav på 14% etter skatt. Morningside betaler 28% selskapsskatt. Selskapet utbetaler 60% av overskuddet etter selskapsskatt i dividende på årets siste dag.
Hva er forventet aksjekurs 31.12.2012 like etter dividendeutbetalingen?
(a) 44,00 kroner
(b) 46,40 kroner
(c) 53,40 kroner
(d) 56,00 kroner
Ettersom vi får oppgitt avkastningskravet etter skatt:
50*1,14 – (24mill*0,6)/4mill = 57 – 3,6 = 53,40 kroner
9. Aksjer i selskapet Nikki ASA koster i dag 80 kroner. Om tre måneder vil kursen enten være 100 kroner eller 80 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 85 kroner og tre måneder til forfall. Risikofri årsrente er 4%.
Hva er salgsopsjonens verdi i dag?
(a) 0,59 kroner
(b) 4,75 kroner
(c) 5,00 kroner
(d) 5,25 kroner
Regn ut dette på samme måte som i de andre innleggene.
ø = 1,25
n = 1,00
Kø = 15
Kn = 0
Husk: årsrente = 4% –> kvartalsrente =1%
Jeg kom frem til at K0 = 0,594
Tar videre utgangspunkt i salg-kjøp paritet
K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf
S0 = 0,594 – 80 + 85/1,01 = 4,75 kroner
10. Aksjer i selskapet Pepper ASA koster i dag 40 kroner. Om tre måneder vil kursen enten være 30 kroner eller 50 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 45 kroner og forfall om tre måneder. Aksjer i selskapet Salt ASA koster i dag 40 kroner. Om tre måneder vil kursen enten være 10 kroner eller 70 kroner. Det omsettes salgs- og kjøpsopsjoner på denne aksjen med innløsningskurs på 45 kroner og forfall om tre måneder. Risikofri årsrente er 4%.
Hvilken av følgende uttalelser er korrekt?
(a) Prisen på kjøpsopsjonen i Pepper er lik prisen på kjøpsopsjonen i Salt.
(b) Prisen på kjøpsopsjonen i Pepper er høyere enn prisen på kjøpsopsjonen i Salt.
(c) Prisen på kjøpsopsjonen i Pepper er lavere enn prisen på kjøpsopsjonen i Salt.
(d) Prisen på kjøpsopsjonene er uavhengig av årsrenten.
Det er lett å se at standardavviket (risikoen) er større i Salt enn i Pepper. Verdien av en opsjon er stigende med økt risiko, så c) er riktig.
11. Markedsverdien av egenkapitalen i Nightlife ASA er 100 million NOK. Det er 5 million utestående aksjer. Kjøps- og salgs opsjoner på aksjene i Nightlife med tre måneder til forfall og en innløsningskurs på 24 NOK, koster i dag henholdsvis 4 NOK og 7,50 NOK.
Hva er tre-måneders risikofri rente?
(a) 2,1%
(b) 2,7%
(c) 4,2%
(d) 4,8%
A0 = 100/5 = 20
K0 – S0 = A0 – I/1+rf
I/1+rf = A0 – K0 + S0
24/1+rf = 20 – 4 + 7,5
24 = 23,5 + 23,5rf
0,5/23,5 = rf
rf = 0,021 = 2,1%
12. Vegaform ASA er 100% egenkapital finansiert. Selskapet har 1 million utestående aksjer med en markedsverdi på $100 per aksje. Vegaform bestemmer seg for å forandre kapitalstruktur. Selskapet låner $60 millioner til 5% rente og bruker lånet til tilbakekjøp av egne aksjer. Lånet er evigvarende. Selskapet betaler 30% selskapsskatt. (Se bort fra investor- og kreditorskatt).
Hva er totalverdien av Vegaform etter forandringen av kapitalstrukturen?
(a) $ 70 millioner
(b) $100 millioner
(c) $118 millioner
(d) $160 millioner
Selskapet tilbakekjøper aksjer for 60 millioner. Dette reduserer antallet utestående aksjer i markedet. I balansen føres tilbakekjøpte aksjer under egne aksjer i form av et negativt tall. Dette vil påvirke selskapsverdien, men ikke aksjeverdien. Hvorfor?
Se for deg at aksjeprisen i dette selskapet er 100 kroner og at det er 1 million utestående aksjer. Verdien til selskapet er da 100 millioner. Dersom selskapet tilbakekjøper aksjer for 10 millioner (altså 100.000 aksjer) vil verdien av egenkapitalen (selskapsverdien i et selskap uten gjeld) være 10 millioner mindre, altså 90 millioner.. Antall utestående aksjer vil være 100.000 færre, altså 900.000. Teoretisk aksjepris vil da være 90.000.000/900.000 = 100
Til oppgaven:
Tidligere var verdien på selskapet:
1.000.000*100 = 100.000.000 dollar.
Balansen påvirkes.
EK: 100.000.000 – tilbakekjøpte aksjer – gjeld
EK: 100.000.000 – 60.000.000 – 60.000.000
EK: -20.000.000
G: 60.000.000
Totalkapital: 60.000.000
Da finnes det flere måter å gjøre dette på. Vi kan f.eks. bruke denne sammenhengen
Verdi av bedrift med gjeld = verdi av bedrift uten gjeld + nåverdi av skattebesparelsen
Skattebesparelsen finner vi slik:
r*PG*Sb / Kg
0,05*60mill*0,30 / 0,05 = 18.000.000
Vm = Vu + NV(skattebesparelse)
Vm = 100.000.000 + 18.000.000 = 118.000.000
Alternativt:
V = 1.00.000*100 + 0,3*60.000.000 = 118.000.000
13. Anor ASA har så langt vært gjeldfritt. Selskapet har betalt dividende på 12 millioner kroner årlig, som tilsvarer hele overskuddet. Egenkapitalkostnaden er 11%, risikofri rente er 4%, og forventet risikopremie er 6%. Anor opptar nå gjeld for 60 millioner kroner til markedsrente på 6%. Lånebeløpet brukes til å tilbakekjøpe aksjer. Ny gjeldsgrad (gjeld/egenkapital) regnet til markedsverdi er 1. Forutsett at M&M-forutsetningene holder, og se bort fra skatt.
Hvordan påvirkes selskapets egenkapitalkostnad av refinansieringen?
(a) Egenkapitalkostnaden blir uendret, 11%.
(b) Egenkapitalkostnaden øker fra 11% til 14%.
(c) Egenkapitalkostnaden øker fra 11% til 15%.
(d) Egenkapitalkostnaden øker fra 11% til 16%.
Ke før = Ku = 11%
[Ke = Ku + (Ku – Kg)*G/EK]
Ke = 0,11 + (0,11-0,06)*1
Ke = 16%
14. Selskapet Trolly ASA er finansiert med egenkapital og gjeld. Verdien av selskapet er gitt ved følgende formel: Vm = Vu + PG*N*⋅
hvor:
VM er verdien av selskapet med gjeld
VU er verdien av selskapet uten gjeld
PG er pålydende gjeld
N er skatteverdifaktoren
Hva er skatteverdifaktoren N under ett-leddsbeskatning?
(a) Den er lik selskapskatten.
(b) Den er lik investorskatten.
(c) Den er lik kreditorskatten.
(d) Den er alltid lik 28%.
N* = n*/(1-Sk)
n* = (1-Sk) – (1-Sb)*(1-SEd)
Dersom det er ettleddsskatt med f.eks Sb=28% er:
n* = (1-0) – (1-0,28)/(1-0)
n* = 1-0,72 / 1
n* = 0,28 = Sb
N* = 0,28/1 = 0,28 = Sb
15. Konsulentselskapet Astro AS har nettopp fått en ny 5-års kontrakt som forventes å gi følgende kontantstrøm etter skatt i de neste 5 årene, (tallene er i millioner kroner):
| Tid | 1 | 2 | 3 | 4 | 5 |
| KS | 100 | 110 | 150 | 170 | 180 |
Denne 5-årskontrakten (prosjektet) krever en investering på 500 millioner kroner. Astro forventer å finansiere prosjektet med egenkapital og et serielån. Astro betaler 5% rente på lånet. Målsatt gjeldandel er 50%. Prosjektets investeringsbeta er anslått til 1,0, markedets risikopremie er 6%, og risikofri rente er 4%. Selskapet betaler 28% skatt. Anta at Modigliani & Millers ett-leddsbeskatning (M&M63) gjelder (sK=sE=0).
Hva er nåverdien av prosjektet dersom det hadde vært 100% egenkapitalfinansiert?
(a) 22,39 millioner kroner
(b) 34,35 millioner kroner
(c) 38,90 millioner kroner
(d) 60,00 millioner kroner
Finner avkastningskravet:
E(Ri) = Rf + (E(Rm) – Rf)*Beta
E(Ri) = 0,04 + 0,6*1
E(Ri) = 10%
Legger inn kontantstrømmen oppgitt i oppgaven (med investeringsutgiften på -500 i år 0) i finanskalkulator med diskonteringsrente 10%
NPV = 22,39
16. Starlight ASA har nettopp akseptert en ny 5-års kontrakt. Denne 5-års kontrakten krever en investering på 400 millioner kroner. Starlight forventer å finansiere prosjektet med egenkapital og gjeld. Starlight betaler 5% renter på gjeld. Gjeldsandelen er 50% og gjelden er et 5-års lån som nedbetales med like avdrag ved utgangen av året. Prosjektets beta er anslått til 1.2, markedets risikopremie er 6% og risikofri rente er 4%. Selskapet betaler 28% skatt. Det er ingen investorskatt.
Hva er nåverdien av renteskattegevinsten? Starlight bruker bokbasert gjeldskapasitet.
(a) 7,51 MNOK
(b) 8,36 MNOK
(c) 8,88 MNOK
(d) 9,53 MNOK
| Tid | 0 | 1 | 2 | 3 | 4 | 5 |
| KS | -200 | 100 | 150 | 170 | 200 | 200 |
| IB lån | 0 | 200 | 160 | 120 | 80 | 40 |
| Avdrag | -40 | -40 | -40 | -40 | -40 | |
| UB lån | 200 | 160 | 120 | 80 | 40 | 0 |
| Rente (5%) | -10 | -8 | -6 | -4 | -2 | |
| Renteskattegevinst | 2,8 | 2,24 | 1,68 | 1,12 | 0,56 |
Legg inn renteskattegevinsten på finanskalkulatoren med diskonteringsrente = lånerente = 0,05
NV = 7,51
17. Selskapet Kenz ASA planlegger å investere i et to-års prosjekt. Investeringen koster 20 millioner kroner, og forventes å gi en kontantstrøm etter skatt på 14 millioner kroner hvert av de to årene. Prosjektets investeringsbeta er anslått til 1,3, markedets risikopremie er 7%, og risikofri rente er 3%. Selskapet betaler 28% skatt. Investorer betaler ikke skatt (sK=sE=0). Prosjektet finansieres med 40% egenkapital og 60% gjeld. Gjelden er et lån til 5%, hele lånet tilbakebetales ved slutten av det andre året.
Hva er prosjektets justerte nåverdi?
(a) ? 3,63 millioner kroner
(b) 0,22 millioner kroner
(c) 3,63 millioner kroner
(d) 3,94 millioner kroner
| 0 | 1 | 2 | |
| Investering/inntekter | -20 | 14 | 14 |
| Lån | 12 | -12 | |
| IB lån | 0 | 12 | 12 |
| UB lån | 12 | 12 | 0 |
| Rente (5%) | 0,6 | 0,6 | |
| Renteskattebesparelse (1) | 0,168 | 0,168 | |
| Sb | 0,28 | ||
| Sk | 0 | ||
| Sed | 0 | ||
| n* | 0,28 |
(1) Renteskattebesparelsen finner du ved: å multiplisere rentebeløpet med n*
n* = (1-Sk) – (1-Sb)*(1-Se)
18. Selskapet New Energy AS ønsker å investere i ny bedrift som skal produsere vindmøller. I første omgang trenger New Energy 12 millioner kroner til et pilot-prosjekt som forventes å ha en levetid på 3 år. Selskapets målsatte gjeldsandel er 60%. New Energy kan låne til 5% rente. I Klekk kommune er det stort behov for nye arbeidsplasser. Den lokale sparebanken tilbyr selskapet New Energy et subsidiert treårig serielån til 2% (billig lån) dersom den nye bedriften etablerer seg i Klekk kommune. Lånet skal nedbetales med like store avdrag hvert år. Se bort fra skatt.
Hva er nåverdien av det subsidierte lånet?
(a) 0,3985 millioner kroner
(b) 0,4252 millioner kroner
(c) 0,5320 millioner kroner
(d) 0,6655 millioner kroner
Her må du sette opp en kontantstrøm for lånet, og neddiskontere det med r=5%
| 0 | 1 | 2 | 3 | |
| Opptak/avdrag | 7,2 | |||
| IB lån | 0 | 7,2 | 4,8 | 2,4 |
| Avdrag | -2,4 | -2,4 | -2,4 | |
| UB lån | 7,2 | 4,8 | 2,4 | 0 |
| Renter (2%) | -0,144 | -0,096 | -0,048 | |
| KS | 7,2 | -2,544 | -2,496 | -2,448 |
Jeg fikk NV = 0,3985 da jeg la det inn på kalkulatoren med diskoteringsrente 5%
19. Selskapene South ASA og North ASA er helt like bortsett fra at South er 100% egenkapital finansiert, mens North har en gjeldsgrad (gjeld/egenkaptial) på 1. Begge selskapene har markedsverdi på 20 millioner kroner. North har en gjeldskostnad på 4%. Forventet, evig overskudd før renter og skatt er 2 millioner kroner i begge selskapene. Se bort fra skatt.
Hva er totalkapitalkostnaden i de to selskapene?
(a) 10% i South og 10% i North.
(b) 10% i South og 14% i North.
(c) 10% i South og 16% i North.
(d) 14% i South og 16% i North.
Kt er uavhengig av finansieringen i et univers uten skatt. Alternativ a) er eneste alternativ hvor Kt i begge selskapene er lik. For ordens skyld:
[V = E(OFRS) / Kt]
Kt = E(OFRS) / V
Kt = 2/20
Kt = 0,10 = 10%
20. Selskapene South ASA og North ASA er helt like bortsett fra at South er 100% egenkapital-finansiert, mens North har en gjeldsgrad (gjeld/egenkapital) på 1. Begge selskapene har markedsverdi på 20 millioner kroner. North har en gjeldskostnad på 4%. Forventet, evig overskudd før renter og skatt er 2 millioner kroner i begge selskapene. Se bort fra skatt.
Hva er egenkapitalkostnaden i de to selskapene?
(a) 10% i South og 10% i North.
(b) 10% i South og 14% i North.
(c) 10% i South og 16% i North.
(d) 14% i South og 16% i North.
Egenkapitalkostnaden (Ke) er imidlertid avhengig av finansieringen. Den vil være økende med økt gjeldsgrad, med mindre gjelden er risikofri.
Ke i South vil være lik Kt, altså 10%
Ke i North kan vi regne ut på to måter:
Alternativ 1:
Ke = Kontantstrøm til eier / EK
Ke = 2.000.000 – (10.000.000*0,04) / 10.000.000
Ke = 1.600.000/10.000.000
Ke = 16%
Alternativ 2:
Ke = Ku + (Ku – Kg)*G/EK
Hvor Ku = totalkapitalkostnad uten gjeld
Ke = 0,10 + (0,10-0,04)*1
Ke = 16%
21. Amerikanske dollar noteres i Paris til 0,7293 og i Oslo til 5,8800. Euro noteres i Oslo til 7,72000.
Hvilken mulig arbitrasjegevinst kan du oppnå hvis du har 1 millioner kroner å investere?
(a) 12.398 kroner
(b) 13.546 kroner
(c) 44.369 kroner
(d) 70.000 kroner
Så:
Dollar:
Paris: EUR/USD = 0,7293
Oslo: NOK/USD = 5,8800
Euro:
Oslo: NOK/EUR = 7,72
Det gir oss krysskurs = EUR/USD * NOK/EUR = NOK/USD –> 0,7293*7,72 = 5,6301960
Vi ser at dollaren er “for dyr” i Norge. (5,5880 mot 5,6301960). Det betyr at vi kan oppnå gevinst ved å først veksle til Euro, så til USD, så tilbake til NOK.
1. Kjøper Euro i Norge for 1 million til kurs 7,72: 1.000.000/7,72 = 129.534 Euro.
2. Veksler disse EUR 129.534 til USD i Paris: 129.534/0,7293 = 177.614 Dollar.
3. Vi selger USD 177.614 i Norge: 177.614*5,88 = 1.044.370,32
Arbitrasjegevinst: 1.044.370,32 – 1.000.000 = 44.370,32
22. Dagskursen mellom enkelte valutaer er som følger:
1 EUR = 1,3300 USD, 1 EUR = 0,7050 GBP, 1 EUR = 0,9300 CHF.
Hva er dagskursen mellom amerikanske dollar og sveitsiske franc, samt mellom sveitsiske franc og britiske pund dersom det ikke foreligger noen arbitrasjemuligheter?
(a) 1 CHF = 1,2369 USD, 1 CHF = 0,6557 GBP
(b) 1 CHF = 0,6815 USD, 1 CHF = 1,3050 GBP
(c) 1 CHF = 0,8051 USD, 1 CHF = 1,5418 GBP
(d) 1 CHF = 1,4301 USD, 1 CHF = 0,7581 GBP
EUR/USD = 1,3300
EUR/GBP = 0,7050
EUR/CHF = 0,9300
EUR/CHF = 0,9300 betyr: CHF/EUR = 1/0,9300=1,0752688
Krysskurs: CHF/USD = CHF/EUR*EUR/USD
CHF/USD = 1,0752688*1,3300 = 1,4301
Krysskurs: CHF/GBP = CHF/EUR*EUR/GBP
CHF/GBP = 1,0752688*0,7050 = 0,7581
23. Den risikofrie årsrenten er 4% i USA og 2% i eurosonen. Dagskursen er 1 EUR = 1,30 USD.
Hva er 12 måneders terminkurs mellom EUR og USD dersom arbitrasjegevinster ikke er mulig?
(a) 1 EUR = 1,2750 USD
(b) 1 EUR = 1,3118 USD
(c) 1 EUR = 1,3255 USD
(d) 1 EUR = 1,4739 USD
[Terminkurs = Spot * (1+rente i hjemlandet) / (1+rente i utlandet)]
Terminkurs = 1,30* (1,04 / 1,02)
Terminkurs = 1,3255
24. Prisen for en kjøpsopsjon med 6 måneder til forfall er kr 12. Innløsningskursen er kr 75. Aksjeprisen på den underliggende aksjen er kr 80, og den risikofrie årsrenten er 5%.
Hva er prisen i likevekt på en tilsvarende salgsopsjon?
(a) kr 3,43
(b) kr 5,19
(c) kr 11,43
(d) kr 18,81
K0 – S0 = A0 – I/1+rf
S0 = K0 – A0 + I/1+rf
S0 = 12 – 80 + 75/1,025
S0 = 5,17
25. Et selskap som er 100% egenkapitalfinansiert er verdsatt til 100 mill. kroner. Selskapets skattesats er 30%.
Hva blir verdien av selskapet dersom det utsteder 50 mill. kroner i evigvarende gjeld og benytter pengene til å kjøpe tilbake aksjer?
(a) 65 mill. kroner
(b) 85 mill. kroner
(c) 100 mill. kroner
(d) 115 mill. kroner
Verdi med gjeld = 100 mill + (50mill*0,3) = 115 mill
26. Et 100% egenkapitalfinansiert selskap har en systematisk risiko målt ved beta på 1,2. Selskapet velger så å endre kapitalstrukturen til 50% egenkapital og 50% gjeld ved å ta opp et lån til 8% rente. Gjeldsbetaen er 0,2. Selskapet er ikke i skatteposisjon.
Hva blir selskapets egenkapitalbeta etter refinansieringen?
(a) 1,2
(b) 1,6
(c) 2,2
(d) 2,4
Ved 100% EK er βe og βt den samme. βe = βt =1,2
[βe = βt + (βt – βg)*G/EK]
– Betaen til totalkapitalen vil ikke ha forandret seg.
– Betaen til gjeld er 0, da gjelden er risikofri (jfr. oppgaveteksten)
βe = 1,2 + (1,2-0,2)*1
βe = 2,2
27. Modigliani og Millers hovedresultat 1 (M&M-1) i en verden uten skatt sier at:
(a) Markedsverdien av et selskap er uavhengig av selskapets kapitalstruktur.
(b) Markedsverdien av et selskaps gjeld er uavhengig av selskapets kapitalstruktur.
(c) Markedsverdien av et selskaps aksjekapital er uavhengig av selskapets kapitalstruktur.
(d) Markedsverdien av et selskaps aksjekapital er lik markedsverdien av selskapets gjeld.
Se innlegget: Gjeldsfinansiering og verdi
28. Selskap X har 100 aksjer utestående. Selskapets årlige resultat er 1.000 kroner som i sin helhet å utbetales som dividende. Denne dividenden forventer selskapet å utbetale i all overskuelig fremtid. Egenkapitalavkastningskravet er 10%.
Hva er forventet aksjekurs i dag?
(a) kr 9,90
(b) kr 90,00
(c) kr 100,00
(d) kr 110,00
V = 1.000 / 0,10 = 10.000
Aksjekurs = 10.000 / 100 = 100 kroner
29. En avgjørende forutsetning for dividendens irrelevans er at:
(a) Ingen usikkerhet om fremtidige aksjekurser.
(b) Det er ingen skatt på kursgevinst.
(c) Kapitalmarkedet er perfekt.
(d) Alle investeringer er risikofrie.
Irrelevansprinsippet sier at under gitte forutsetninger vil det ikke være mulig å påvirke verdien av et selskap gjennom dividendepolitikk. Den påstår at det er et nullsumspill som gjør at effekten av dividendeendring vil nøytraliseres av en tilsvarende endring i aksjekurs. Forutsetningene er:
1) Kapitalmarkedet er perfekt, men det kan være skatt på bedrifter og investorer.
2) Egenkapitalbeskatningen er nøytral.
3) Alt annet enn dividendepolitikken holdes konstant (dividendepolitikken påvirker inne investerings- og gjeldsgradsbeslutninger).
30. Et stort selskap mottar en lånegaranti fra staten. Med denne garantien er selskapet i stand til å låne 50 mill. kroner over fem år til 8% årsrente i sted for markedsrenten som er 10% per år.
Hvilken verdi har denne lånegarantien for selskapet? Se bort fra skatt.
(a) +53.79 mill. kroner
(b) +3.79 mill. kroner
(c) -3.79 mill. kroner
(d) -53.79 mill. kroner
| 0 | 1 | 2 | 3 | 4 | 6 | |
| Opptak/avdrag | 50 | |||||
| IB lån | 0 | 50 | 50 | 50 | 50 | 50 |
| Avdrag | -50 | |||||
| UB lån | 50 | 50 | 50 | 50 | 50 | 0 |
| Renter (8%) | -4 | -4 | -4 | -4 | -4 | |
| KS | 50 | -4 | -4 | -4 | -4 | -54 |
Regn ut nåverdien av kontantstrømmen med diskonteringsrente 10%
NV = 3,79 millioner kroner


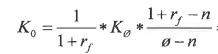

I oppg 10, hvordan ser du at std, altså risiko er større i Salt? Regnet du det ut? I så fall hvordan? Jeg prøvde å regne ut varians utifra opplysningene oppgitt, men får det ikke til
Spm: Du ser at differansen mellom laveste og høyeste verdi om tre måneder er større. I Pepper kan aksjen endre seg med 10 kroner opp eller ned. I Salt er aksjebevegelsen mye større, som gir høyere risiko.
I oppgave 24. Hvorfor har du at rf blir 1,025? må man endre renten? Burde det ikke vært 1,0125 i tilfelle? Skjønner ikke.
Victoria: Risikofri årsrente er 5%. Da må risikofri rente for et halvt år bli 2,5%. 1 + 0,025 = 1,025.
På oppgave 16:
– Hvordan regnet du ut renteskattegevinsten? Hva er n* i dette tilfellet?
– I noen oppgaver står det ikke Se eller SK, eks står SK=SE=0, hvordan regner man ut n* i disse tilfellene?
– Hvorfor har du brukt lånerenten som diskonteringsrente fremfor KE som er vanlig?
Takker for svar!
ole:
– rente*Sb
– Du kan fremdeles regne n* = (1-Sk) – (1-Sb)*(1-Se)
– Det er ikke investorskatt, så n* = Sb.
– Det er ikke vanlig å bruke Ke som diskoteringsrente. Du bruker Kt når du regner NV av investeringen, og renten når du regner NV av finansieringen.
Men høst 2013 bruker du jo KE? Samme i høst 2011 oppgave 9.
–> E(Ri) = 0,04 + 0,07*1,2 = 12,4%, E(Ri) er jo ofte = KE?
Med Kt mener du Totalkapitalkostnad? Hvilken formel bruker du isåfall da, Kt = ke*we + kg*wg?
ole: E(Ri) er forventet avkastning fra investeringen. Den modellen kalles kapitalverdimodellen og kan brukes til å finne både Ke, Kt og Kg. Jeg bruker som regel E(Ri) til å finne Kt, da det er den som brukes til å neddiskontere kontantstrømmen når du skal finne NV av en investering. Husk at Ke = Kt når du er 100% EK-finansiert. Les dette innlegget: http://hobbyokonomen.blogg.no/1480082961_finansiell_styring__g.html
Du er en gud
Bare ett spørsmål: Når skal man finne diskonteringsrente ved Kt og når skal man bruke renten som er på lånet, slik du gjør i denne oppgaven?
ole: Du neddiskonterer med renten på lånet når du skal finne NV av renteskattegevinsten f.eks. Kt må du neddiskontere med hvis du f.eks. skal finne NV av en investering.
Ok. Takk! Fantastisk blogg. Sikkert veldig lærerikt også.