Hei.
Her kommer litt hjelp til AK2 i metode og økonometri.
A:
Lag dummyvariabler:
gen d1=fortype==1
gen d2=fortype==2
gen d3=fortype==3
gen d4=fortype==4
B:
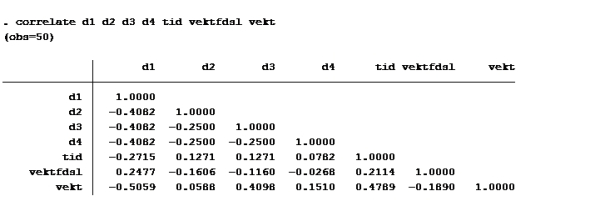
Korrelasjonsmatrise:
1)
2)
C:
D:
E:
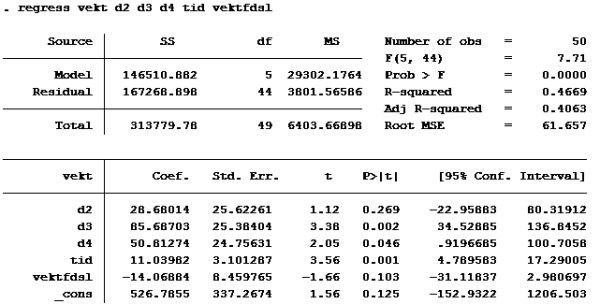
T-test: En t-test brukes til enkel hypotesetesting. Det vil si at man bare tester én koeffisient av gangen. Nullhypotesen i en t-test er gitt ved likhet, dvs. at koeffisienten det er snakk om antas å være lik en viss verdi. Enkelt kan vi bare se på P>|t|. De variablene med p>|t| over 0,05 skal ut. Det betyr at d2 og vektfdsl skal ut.
Da får vi:
F:
Vi må generere en variabel med den naturlige logaritmen til vekt og vektfdsl:
Det gjør vi ganske enkelt med kommandoene:
gen lnvekt=ln(vekt)
gen lnvektfdsl=ln(vektfdsl)
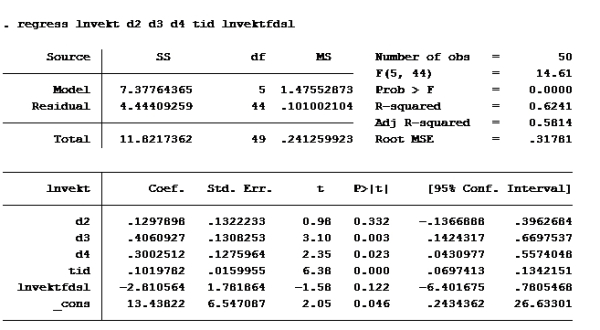
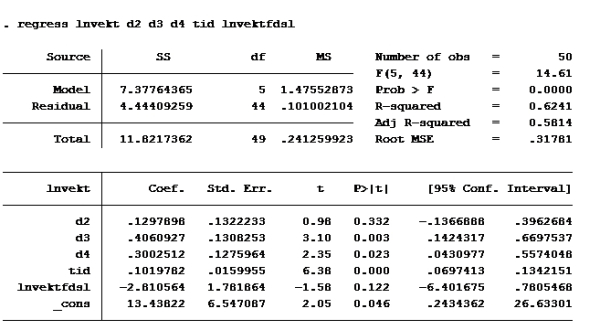
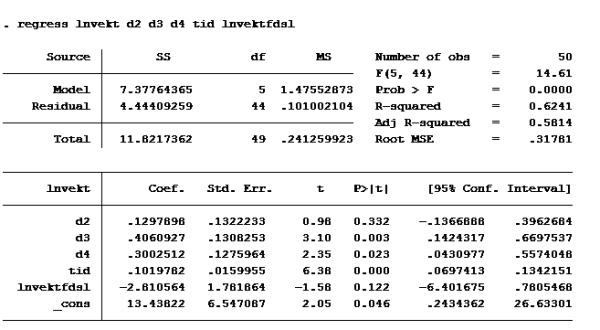
Deretter kjører vi regresjonen de ber om:
G:
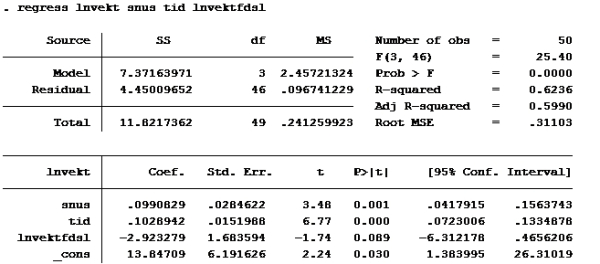
Lager først ny variabel med (d2+4*d3+3*d4). Kaller den bare «snus», fordi det er gøy.
gen snus=d2+4*d3+3*d4
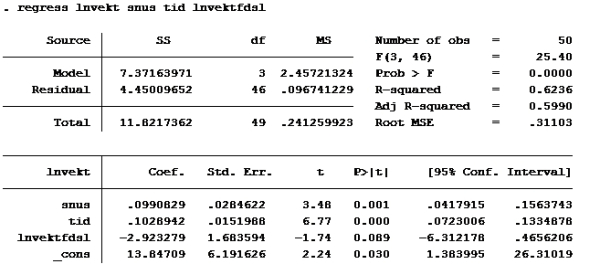
Kjører deretter regress:
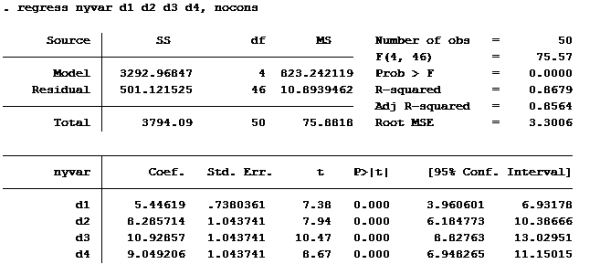
H:
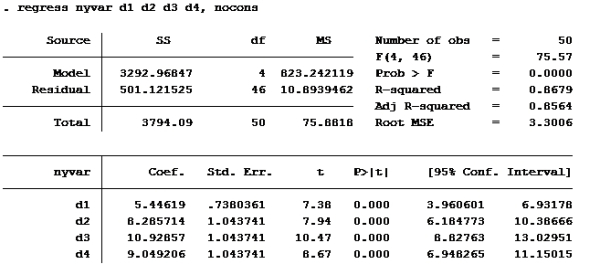
Lager den nye variabelen de ber om. Kaller den “nyvar”
gen nyvar=(vekt-vektfdsl)/tid
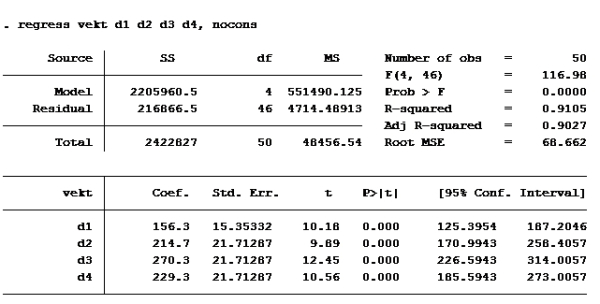
Kjører deretter regresjon med suppressed cons (nocons):
Da var det gjort. Så var det oppgavene:
Oppgave 1:
Her er det et spørsmål om variablenes målenivå. Det at variablen er på forholdsnivå (skalanivå) betyr at en i tillegg til å rangere og måle f.eks avstand også kan beregne forholdstall. For eksempel er variabelen inntekt på forholdstallsnivå. (Noen som tjener 200 000 har dobbelt så stor inntekt som noen som tjener 100 000). Vekt og tid kan også måles som forholdstall, mens fôrtype ikke kan det.
Riktig svar er d
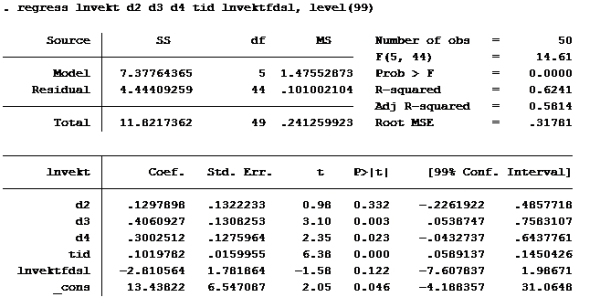
Oppgave 2:
Kjører ny regresjon med 99% konfidensintervall:
Her ser vi at konfidensintervallet til lnvektfdsl er [-7,607837; 1,98671]
Alternativt manuelt:
t=0,01/2, 50-6 = 2,692 (t-tabell)
[b6- t=0,01/2, 50-6*SE(b6), b6 + t=0,01/2, 50-6*SE(b6)]
[-2,810564 – 2,692*1,781867, -2,810564 + 2,692*1,781867]
[-7,607837, 1,98671]
Oppgave 3
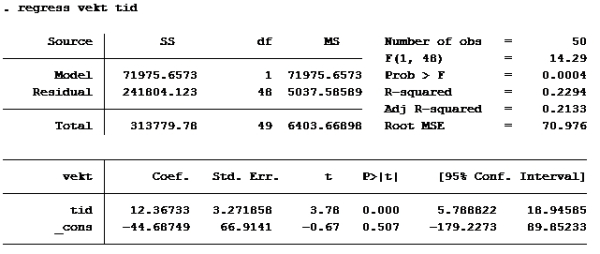
Her må vi se hvilken modell som har høyest forklaringskraft (uttrykt ved r-squared)
a)
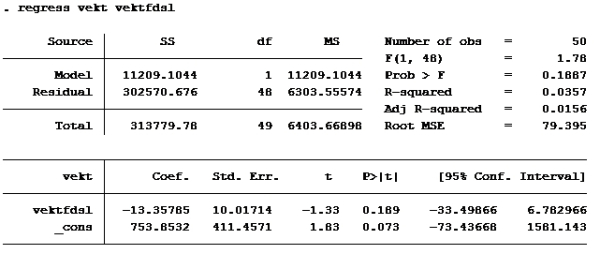
b)
c)
d)
Som vi ser har modell d) høyest r-squared.
Alternativ d er riktig
Oppgave 4
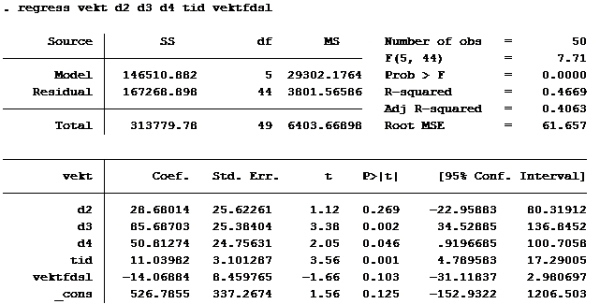
Modell D igjen:
Som vi allerede så er d2 og vektfdsl ikke signifikante på 5% nivå. (P>|t| er større enn 0,05). De andre er det. d4 er imidlertid ikke signifikant på 1% nivå (P>|t| er større enn 0,01 på d4)
Alternativ b er riktig.
Oppgave 5:
Modell H
Bare se på koeffisienten til d4, den er ca 9.
alternativ d er riktig
Oppgave 6
Modell F
Her må du pålegge modellen følgende restriksjoner:
B3 = 4B2 og B4 = 3B2
Fordi:
Hvis vi løser opp parentesen B2(d2+4d3+3d4) får vi:
B2*d2 + 4B2*d3 + 3B23*d4
Regresjonen er egentlig:
ln(vekt) = B1 + B2*d2 + B3*d3 + B4*d4 + B5*tid + B6*lnvektfdsl
–>Setter inn 4B2 for B3 og 3B2 for B4:
ln(vekt) = B1 + B2*d2 + 4B2*d3 + 3B2*d4 + B5*tid + B6*lnvektfdsl
Alternativ b er riktig.
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
Oppgave 7
Modell F
Modell G
Sjekk der det står residual. Der står det 4,444 på modell F og 4,4500 på modell G
Benytter F-test (multippel hypotesetesting, som innebærer at man tester flere koeffisienter av gangen).
testobservator finner vi ved:
(RSSmed – RSSuten) / m) / ((RSSuten / (N – K ))
hvor m er antall hypoteser/restriksjoner, N er antall observasjoner og K er koeffisienter i regresjonsmodellen (uten restriksjoner)
RSSmed er RSS med restriksjoner, og RSSuten er RSS uten restriksjoner.
RSSmed er det du får når du kjører modellen med «snus» (altså modell G), da den pålegger modellen restriksjoner.
RSS uten er det du får når du kjører uten restriksjoner, altså lnvekt d2 d3 d4 tid lnvektfdsl
Vi har jo følgende tall:
N er 50 (50 observasjoner)
K er 6 (6 Ber)
m: 2 (2 restriksjoner, B3 = 4B2 og B4 = 3B2)
RSSmed er 4,45009652
RSSuten er 4,44409259
(RSSmed – RSSuten) / m) / ((RSSuten / (N – K ))
((4,45009652 – 4,44409259 ) / 2) / (4,44409259 / (50 – 6)) = 0,0297218065
Slå opp i tabellene på 1%, 5% og 10% signifikansnivå og se på m=2 og N-K = 44 (i tabellen er ikke 44 med, men se på 40) for å se om noen av verdiene der er lavere enn 0,0297218065. Er de lavere, forkastes nullhypotesen. Jeg får henholdsvis verdiene 5,18, 3,23 og 2,44 . Ingen av dem er lavere enn testobservator, som betyr at nullhypotesen ikke forkastes på noen av de tre signifikansnivåene.
Riktig alternativ er a
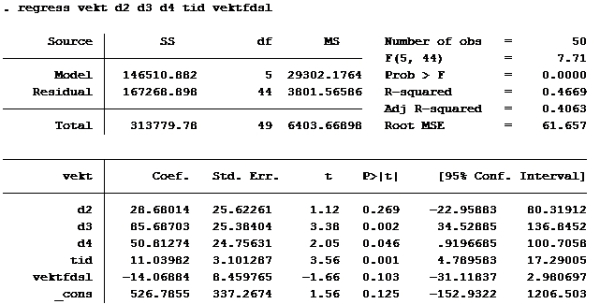
Oppgave 8
Modell D:
Setter inn: B2=0 B3=1, B4=0, B5=21, B6=41,06:
526,7855 + 28,6801*0 + 85,6870*1 + 50,8127*0 + 11,0398*21 – 14,06884*41,06 = ca 267
Alternativ c er riktig
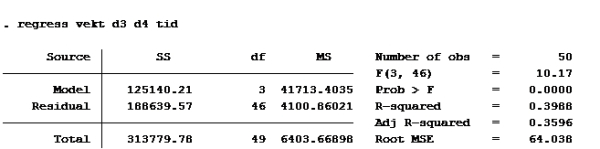
Oppgave 9
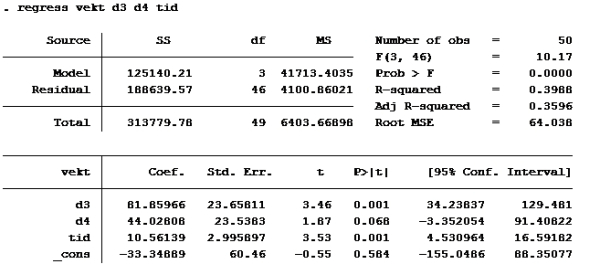
Modell E
Setter inn: B2=1, B3=0, B4=21
-33,3489 + 81,8597*1 + 44,0281*0 + 10,5614*21 = ca 270
Alternativ c er riktig
Oppgave 10:
Hvis vi ser på regresjonene for C, D og E ser vi at koeffisienten til d3 er den som er størst (positiv). Det vil med andre ord si at effekten er størst for fôrtype 3.
Eks:
Alternativ c er riktig her også
Oppgave 11:
Her er det en lineær sammenheng
Endring Y = endring B2*endring X
Bare test:
Yhatt = 1,08 + 0,19X2 + 33,64lnX3 + 68,11
Dersom vi øker C2 med én enhet, og lar alle de andre X-ene være uforandret ser vi at Yhatt vil øke med 0,19. De andre alternativene er derfor sikkert feil.
Alternativ d er riktig
Oppgave 12
Lin-log (Lineær venstreside, logaritme på høyreside)
Vi ser at ved endring på 1%:
Endring Y = B3*1%
Endring Y = 33,64*0,01=0,3364
Alternativ c er riktig
Oppgave 13:
Resiprok-modell:
Endring Y = 68,11*(1/11) – 68,11*(1/10) = -0,60818
For å se endringen ved økning fra 10 til 11
Alternativ a er riktig
Oppgave 14
Dersom man setter alle koeffisientene lik 0 vil alltid R^2 være 0. Logikken er at R^2 er forklaringskraft, dersom man setter alle de uavhengige variablene lik 0, slik at regresjonsmodellen bare inneholder konstantleddet vil ikke modellen ha noen forklaringskraft. For den som vil ha litt mer kjøtt på beinet her:
R^2 kan regnes ut ved: 1 – (RSS/TSS). Hvor RSS er residualsummen og TSS er totalkvadratsummen. Når regresjonen KUN inneholder konstantleddet kan det vises at RSS = TSS, altså at RSS/TSS = 1, og at R^2 = 1-1= 0.
Fun fact: selv om R^2 er «opphøyd i andre», betyr ikke det at R^2 ikke kan være negativ. I enkelte tilfeller, hvor konstantleddet ikke inkluderes kan faktisk R^2 være negativ. Dette betyr at man har «negativ forklaringskraft». Sjukt å melde?
Oppgave 15:
Vi bruker F-testen for multippel hypotesetesting og finner kritiske verdier for signifikansnivåene:
*3 restriksjoner (m)
*44 observasjoner (N)
*4 koeffisienter uten restriksjoner(K)
Ser i F-tabellene:
F1%, 3, 44-4 = 4,31
F5%, 3, 44-4 = 2,84
F10%, 3, 44-4 = 2,23
Det betyr at alternativ d må være riktig.
Oppgave 16
Ser i F-tabellene:
F1%, 3, 44-4 = 4,31
F5%, 3, 44-4 = 2,84
F10%, 3, 44-4 = 2,23
Hvis testverdien i forrige oppgave er 2,839 ( altså ca 2,84) er p-verdien ca 5%
Alternativ b er riktig
Oppgave 17
| Parameter | Kritisk verdi | Observasjonsverdi | Konklusjon |
| b2 | T0,005, 29-3 = 3,707 (t-tabell) | T-obs = (b2 – 0) / SE(b2) T-obs = 0,5174 – 0 /0,1270 T-obs = 4,0740 | H0 forkastes P-verdi veldig liten (mindre enn 0,1%) |
| b3 | T0,10, 29-3 = 1,315 (t-tabell) | T-obs = (b3 – 0) / SE(b3) T-obs = 0,0037-0 / 0,0044 T-obs = 1,3 | H0 beholdes p-verdi veldig stor (større enn 20%) |
Her skal jeg innrømme at jeg er litt usikker på svaret, men regelen er jo at når H0 forkastes, så har vi grunnlag for å hevde at det er lineær samvariasjon mellom den uavhengige variabelen og den avhengige variabelen.
Konklusjonen blir derfor så vidt jeg kan forstå at det er en lineær sammenheng mellom X og Y.
Alternativ c er riktig (tror jeg)
Oppgave 18
Dersom vi har en kvalitativ variabel med m ulike verdier, kan vi IKKE inkludere konstanten B1 dersom vi skal inkludere m dummyvariabler.
Dersom vi har en kvalitatativ variabel med m ulike verdier, kan vi inkludere konstanten B1 dersom vi kun inkluderer m-1 dummyvariabler
Alternativ d er riktig fordi der har de m dummyvariabler + konstantledd.
Oppgave 19
58,73 – 9,21*0 + 38,44*0 = 57,73 = ca 59
Oppgave 20
Bruker F-test
Nullhypotesen er at B2 = 0 og B3 = 0
Alternativhypotesen er at en eller begge påstandene i H0 er feil.
Vi har:
m = 2
N-K = 68-3 = 65
Kritiske verdier
F1% = 4,98
F5% = 3,15
F10% = 2,39
Testverdien
(R^2uten – R^2med) / m) / ((1-R^2 uten/ (N – K ))
R^2 med restriksjoner vil være 0 når bare konstantleddet står igjen.
Testverdi = ((0,08 – 0)/2) / ((1-0,08)/65)
Testverdi = 2,82
Konklusjonen blir at på signifikansnivåene 1% og 5% beholdes H0 om at gjennomsnittlig antall klikk kan være lik for de tre reklamene (fordi testverdi er mindre enn kritisk verdi). På et 10% signifikansnivå forkastes derimot H0.
Alternativ c er riktig






Utrolig enkelt å forstå. TUSEN TAKK!
Vil du gjøre det samme med eksamens oppgaven som kommer ut 2 uker før eksamen?
Robert: Hei! Ja, det kommer jeg garantert til å gjøre. Følg med på bloggen for mer info 🙂
Tusen takk!! Vil være fantastisk om du gjør det samme med eksamensoppgaven når den tid kommer 😀
Du er en levende legende, vet du det?
Tusen hjertelig!
Eksamen kommer 25/5. Når tror du sån cirka du er klar med den?
Richard: Caset har jeg klart samme dag som den kommer ut.
Hei, kommer du til å gjøre caset som kom ut i metode og økonometri i dag? Sliter med de to siste oppgavene..
Helt amazing hvis du klarer å legge ut eksamenscaset! Fantastisk blogg 🙂
Det kom ut i går 🙂
Hei! Legge du ut eksamens casen i år også ? 🙂
Lars: Ja, så lenge noen sender meg caset.
hobbyøkonomen: jeg elsker deg
Godt nytt år Hobbyøkonomen! mine beste ønsker til deg 🙂
Jeg lurer på om du skal redde oss i Metode i dette semesteret?
La meg uansett takke deg for “back us up”. Du er min helt! Nå går jeg 2. året 🙂
FFM: Jeg skal hjelpe dere med caset til eksamen om ikke mer 🙂
Hei! Veldig lærerik blogg du har!
Vil du legge ut hjelp/løsningsforslag til case til eksamen i dette faget nå i vår? 🙂
Det er planen =)
Hei på deg!
Kunne du ha sett gjennom Arbeidskrav 2 for vår 2018?
Jeg lærer utrolig mye av å se forklaringene dine, men skulle gjerne hatt enda mer step by step ift Stata. Om du ser at du har tid: På forhånd tusen takk 🙂
Tove: Hei. Har ikke fått oversendt arbeidskrav 2, men har dessverre ikke tid til å se på det nå, pga eksamener som nærmer seg. Lover at jeg skal se på caset deres og lage en løsning til det når det kommer ut! Bare send meg en mail når det er publisert 🙂
Hva mener du med b6 i oppgave 2?
Line: b6 er koeffisienten til variabelen “lnvektfdsl”
Hei Hobbyøkonomen! Vi elsker deg. Du har nå reddet oss gjennom 2 år, med gode karakterer vi aldri hadde klart uten deg<3 Kunne du lagt ut caset for eksamen 2019 også? Da hadde du reddet livet vårt nok engang. Klemklem
I fix.
Hei,
Har du mulighet til å se på vårens eksamenscase som kom ut i dag?
Og hvordan kan jeg evt sende deg det?
Ha en fin dag 🙂
Hei. Det er løst. Se her: https://hobbyokonomen.blogg.no/caselosning-met3590-var-2019.html
Kommer du til å legge ut en løsning på eksamen?😊
Nei, det var ikke planen.
Hei, legger du ut løsning på eksamenscaset i år også? 🙂 vi sliter veldig med STATA hehe
Jupp 🙂
Hei, kommer du til å legge ut løsningsforslaget på eksamenscaset i metode og dataanalyse i år?
Hvis noen sender meg caset 🙂
Hei, kommer du til å gå gjennom eksamenscaset iår også? (vår 2023)
Ja 🙂