Her er endelig arbeidskrav 8.
Vi benytter følgende tall til de neste oppgavene:
En bedrift benytter standardkostkalkyler og ? regnskap i sin økonomistyring. Bedriften produserer ett produkt. Standard bidragskalkylen per enhet ferdigvare for produktet for året 20×1 så slik ut:
Direkte materialkostnader (DM) (4 kg a kr 125) kr 500
Direkte lønnskostnader i T 1 (DL 1) (2 timer kr 150) kr 300
Direkte lønnskostnader i T 2 (DL 2) (3 timer a kr 200) kr 600
Indirekte variable kostnader i T 1 (2 t a kr 50) kr 100
Indirekte variable kostnader i T 2 (50 % av DL 2) kr 300
Variable tilvirkningskostnader (VTVK) kr 1 800
Indirekte variable salgs- og adm.kostnader. (10 % av VTVK) kr 180
Totale variable kostnader kr 1 980
Budsjettert salgspris kr 3 300
Budsjettert dekningsbidrag kr 1 320
Budsjetterte faste kostnader for året 20×1 utgjorde i hver avdeling:
Tilvirkningsavdeling 1 (T 1) kr 4 800 000
Tilvirkningsavdeling 2 (T 2) kr 6 000 000
Salgs- og adm. avdeling kr 3 600 000
Sum faste kostnader kr 14 400 000
Budsjettert salg for januar måned 20×1: 1 800 enheter
Virkelig produksjon og salg i januar 20×1:
Satt i produksjon 1 500 enheter
Ferdigprodusert 1 400 enheter
Solgt 1 550 enheter (Salgsinntekten var kr 4 417 500)
En enhet varer i arbeid har fått tilsatt alle materialene og er 75% ferdig bearbeidet i tilvirkningsavdeling 1, men ikke påbegynt i tilvirkningsavdeling 2. Når driftsregnskapet settes opp etter bidragsmetoden, verdsettes beholdningene av tilvirkede varer til standard variable tilvirkningskostnader. Når driftsregnskapet settes opp etter selvkostmetoden, verdsettes beholdningene av tilvirkede varer til standard totale tilvirkningskostnader.
Virkelige kostnader i januar 20×1 utgjorde:
| Variable | Faste | |
| Direkte material ( 5 775 kg) | 721 875 | |
| Direkte lønn i T 1 (2 875 t) | 523 250 | |
| Direkte lønn i T 2 (4 040 t) | 735 280 | |
| Tilvirkningsavdeling 1 | 133 750 | 423 000 |
| Tilvirkningsavdeling 2 | 380 000 | 511 000 |
| Salgs- og adm avd | 261 400 | 300 000 |
Oppgave 1
Hva var budsjettert produksjonsresultat for januar 20×1? Oppgi svaret (kun tallet) i hele kroner og bruk punktum som tusenskiller.
Vi blir spurt om budsjettert produksjonsresultat. Altså ønsker de at vi skal fortelle hva man budsjetterer at resultatet skal bli. Det er ikke noe vits å tenke at dette må være noe mer komplisert enn det har vært tidligere, bare fordi det denne gang er snakk om en «standardkost-oppgave».
Resultatet er jo inntekt – kostnad som alltid før.
Altså må vi ta de budsjetterte inntektene vi har, og trekke fra de budsjetterte kostnadene våre.
Sagt på en annen måte:
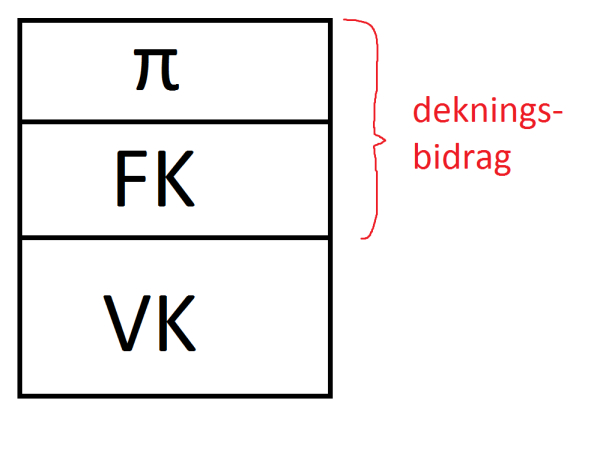
Dekningsbidrag – FK.
Budsjettert DB pr enhet finner vi ved å ta (pris-VEK)
Som vi ser er budsjettert salgspris 3.300. Budsjetterte VEK er 1.980. Da skulle DB bli 1.320 (noe de forsåvidt også har regnet ut for oss, men fint med en repetisjon, ey?). Ganger vi dette med antall enheter vi budsjetterer å selge (1800) får vi
Så må vi trekke fra de faste kostnadene, og de er oppgitt til å være 14.400.000 pr år. Altså, for å finne ut hva vi budsjetterer de faste kostandene til å være i januar måned, må vi nesten dele på 12.
Tar du DB – FK nå, så skal du se då får riktig svar på oppgaven.
Oppgave 2
Hva utgjør standard materialforbruk i kg i januar måned? Svaret (kun tallet) oppgis i kg uten benevning og uten desimaler. Bruk punktum som tusenskiller.
Vi blir spurt om standard materialforbruk i kg. Altså hva som er det standardiserte materialforbruket gitt faktisk produksjon. Når det dukker opp slike oppgaver er det viktig å ta en titt på informasjonen som forteller oss noe om hvordan produksjonen er fordelt på de forskjellige tilvirkningsavdelingene (i dette tilfellet T1 og T2).
Denne gangen ser vi at varer i arbeid, altså «VIA», har fått tilført all materiale i tilvirkningsavdeling 1. Det betyr at 100% av material er medgått i produksjonen i en tidligere periode, og at 75% av arbeidet er gjort (ergo er 75% av timene har blitt «arbeidet» i en tidligere periode).
Det betyr videre at vi bare trenger å regne med de enhetene vi har satt i produksjon når vi skal finne standard materialforbruk. Dette fordi ALLE enhetene som blir satt i produksjon denne perioden blir tilført 100% av materialene de trenger. At bare 1400 av disse ble ferdigstilt, betyr ingenting – fordi alle 1500 enheter fikk tilført 100% av materialet i perioden.
Det betyr ganske enkelt at vi bare trenger å gange enheter satt i produksjon med antall kg pr enhet. Lykke til
Oppgave 3
Hva utgjør standard materialforbruk i kr i januar måned? Svaret (kun tallet) oppgis i kr uten benevning og uten desimaler. Bruk punktum som tusenskiller.
For å finne standard materialforbruk i kg ganger du antall kg du har brukt (som du fant i oppgave 2) med antall kroner det koster pr kg!
Oppgave 4
Hva utgjør standard timeforbruk i tilvirkningsavdeling 1 i januar måned? Svaret (kun tallet) oppgis i timer uten benevning og uten desimaler. Bruk punktum som tusenskiller.
Standard timeforbruk i T1 finner du enkelt ved å se på hvor mange timer som brukes på en enhet i tilvirkningsavdeling 1. Det er da viktig å skille mellom en vare i arbeid («VIA») og en ferdigvare («FV»)
For en VIA ser vi at 75% av jobben allerede er gjort i en tidligere periode (se for deg at den er satt på et lager etter at den er 75% ferdigarbeidet, og at du i januar tok den ut for å gjøre den ferdig). Det betyr at vi må gjøre følgende regnestykker:
Timeforbruk FV = (ferdigprodusert*antall timer som brukes pr enhet i T1)
Timeforbruk VIA = (satt i produksjon – ferdigprodusert *(antall timer*0,75)
Finner du disse to, og legger dem sammen, har du svaret ditt.
Oppgave 5
Hva utgjør standard direkte lønnskostnader i tilvirkningsavdeling 2 i januar måned? Svaret (kun tallet) oppgis i kroner uten benevning og uten desimaler. Bruk punktum som tusenskiller.
Javel, så hva med T2, tenker du! Samme som T1? Ikke helt. Her skal svaret oppgis i antall kroner. Vi ser av informasjonen at VIA ikke har vært innom T2 i det heletatt. Det betyr ganske greit at alle de ferdigproduserte enhetene har vært innom T2 denne perioden (og bare de, fordi de 100 enhetene som ble satt i produksjon, men ikke ferdigstilt fortsatt «står på lager».)
Da tar du ganske enkelt: (ferdigproduserte enheter*lønnskostnadene i T2)
Oppgave 6
Hva utgjør effektivitetsavviket for indirekte variable kostnader i tilvirkningsavdeling 1 i januar måned? Svaret (kun tallet) oppgis i kr uten benevning og uten desimaler. Bruk punktum som tusenskiller. Hvis avviket er negativt, markerer du det ved å sette minustegn foran beløpet. Hvis avviket er positivt (gunstig), setter du ikke fortegn foran beløpet.
Effektivitetsavviket blir vi spurt om her. Effektivitetsavviket på de indirekte variable kostnadene skyldes over- eller underforbruk av direkte timer i forhold til forventningene (da direkte timer er aktivitetsmålet som uttrykker effektiviteten i våre oppgaver)
Effektivitetsavvik indirekte variable kostnader = (standard tid*standard tilleggssats i kr) – (virkelig tid * standard tilleggssats i kr)
Vi har en tilleggssats for indirekte variable kostnader på 50 kroner pr direkte time.
Periodens standard direkte timer er beregnet til ??? (dette fant vi i oppgave 4).
Virkelig direkte timer utgjør 2.875 (oppgitt i oppgaveteksten).
Lykke til!
Har du nytte av bloggen? Vipps en kaffekopp eller et valgfritt beløp:
Vipps: 536077
Eller via Ko-fi: Ko-fi.com/hobbyokonomen
Oppgave 7
Hva utgjør forbruksavviket for indirekte variable kostnader i tilvirkningsavdeling 2 i januar måned? Svaret (kun tallet) oppgis i kr uten benevning og uten desimaler. Bruk punktum som tusenskiller. Hvis avviket er negativt, markerer du det ved å sette minustegn foran beløpet. Hvis avviket er positivt (gunstig), setter du ikke fortegn foran beløpet.
Vi blir spurt om forbruksavviket for indirekte variable kostnader i tilvirkningsavdeling 2. I vårt tilfelle har vi en prosentsats for indirekte variable kostnader i T2, på 50%. Da får vi følgende formel:
Forbruksavvik = ((Tid virkelig * Lønn standard) * Tilleggssats) – Virkelige indirekte variable kostnader
Forbruksavvik = ((????*???)*0,5) – 380.000
Forbruksavvik= ?
Oppgave 8
Hva utgjør beholdningsendringen i kroner for varer i arbeid i januar måned forutsatt at bedriften har satt opp sitt driftsregnskap etter bidragsmetoden? Svaret (kun tallet) oppgis i kr uten benevning og uten desimaler. Bruk punktum som tusenskiller. Hvis det er en nedgang i beholdningen, setter du et minustegn foran beløpet. Hvis det er en økning, setter du ikke fortegn foran beløpet.
For å finne beholdningsendring i kroner, er det lurt å først finne beholdningsendring i antall enheter.
Det er ganske enkelt. Du må bare se på hvor mye større eller mindre lagret ditt er på slutten av måneden sammenlignet med starten av måneden. Også her er det nødvendig å skille mellom VIA og FV.
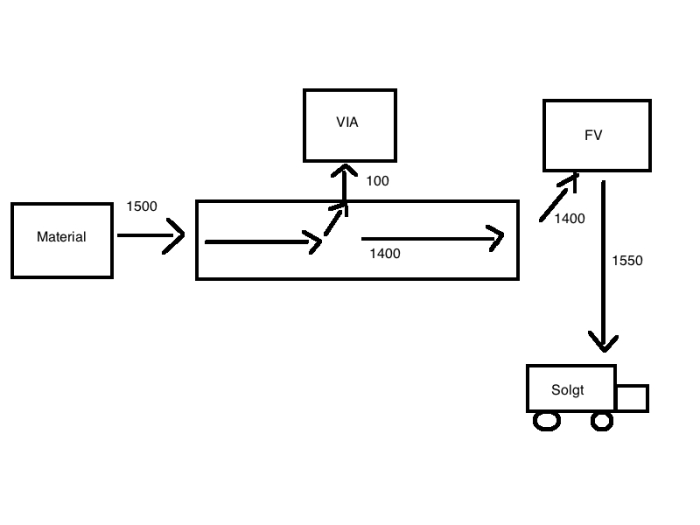
Jeg har laget en nydelig Paint-tegning som kanskje kan gjøre dette litt lettere å forstå. Boksene med “material”, “VIA” og “FV” er lager for henholdsvis material, varer i arbeid og ferdigvarer. Den litt lengre boksen skal være et samlebånd. Det siste er en lastebil. Jeg er ingen kunstner.
I vår oppgave har vi satt i gang hele 1500 enheter, så vi legger i første omgang material til 1500 enheter på samlebåndet. Deretter, underveis på samlebåndet tar vi av 100 enheter for å legge dem på VIA-lageret vårt, slik at vi kan fortsette produksjonen senere. Vi får altså en økning på (1500-1400=100) enheter VIA i beholdningsøkning. De 1400 ferdigvarene settes på ferdigvarelageret vårt.
Men, så skjer det ting, vi selger 1550 enheter, det vil si at etter vi satte 1400 ferdigvarer inn, så tar vi 1550 ferdigvarer ut. Følger vi denne tankerekken ser vi at vi har fått (1400-1550 = -150) ferdigvarer mindre på lager.
Beholdningsendring i antall enhet er derfor slik:
Beholdningsendring VIA: +100
Beholdningsendring FV: -150
Det er VIA vi blir spurt om i oppgaven, og derfor må vi finne ut hva en VIA er verdt forutsatt at vi bruker bidragsmetoden (som i praksis betyr at vi ikke regner med de faste kostnadene). Vi skjønner at verdien av VIA består av materialkostnadene, lønnskostnadene og de indirekte variable kostandene
VIA materialkostnad: 500
VIA lønnskostnad: 300*0,75 = 225 (fordi vi anvender bare 75% av arbeidstimene i T1 på VIA)
VIA indirekte variable kostnader: 100*0,75=75
=VIA verdi: 800
En VIA er altså verdt 800 kroner, og vi har fått 100 flere på lager. Hva tror du verdien av “VIA-hylla” på lageret vårt har økt med?
Oppgave 9
Hva utgjør beholdningsendringen i kroner for ferdigvarer i januar måned forutsatt at bedriften har satt opp sitt driftsregnskap etter bidragsmetoden? Svaret (kun tallet) oppgis i kr uten benevning og uten desimaler. Bruk punktum som tusenskiller. Hvis det er en nedgang i beholdningen, setter du et minustegn foran beløpet. Hvis det er en økning, setter du ikke fortegn foran beløpet.
Ferdigvarene på lager er verdt 1800 (VTVK). Vi har fått 150 mindre siden starten av måneden. Hvor mye mindre er “FV-hylla” vår verdt? Enkelt regnestykke, lykke til. Husk negativt fortegn.
Oppgave 10:
| Resultatregnskap for året | 20×1 | |
| Driftsinntekter | 70.000.000 | |
| Driftskostnader | 58.000.000 | |
| Driftsresultat | 12.000.000 | |
| Renteinntekter | 150.000 | |
| Rentekostnader | 2.050.000 | |
| Resultat før skattekostnad | 10.100.000 | |
| Skattekostnad | 2.727.000 | |
| Årsresultat | 7.373.000 | |
| ||
| Balanse per 31.12. | 20×1 | 20×0 |
| Anleggsmidler | 76.000.000 | 65.000.000 |
| Omløpsmidler | 30.000.000 | 25.000.000 |
| Sum eiendeler | 106.000.000 | 90.000.000 |
|
| |
| Egenkapital | 33.700.000 | 30.000.000 |
| Langsiktig gjeld | 42.000.000 | 34.000.000 |
| Kortsiktig gjeld | 30.300.000 | 26.000.000 |
| Sum egenkapital og gjeld | 106.000.000 | 90.000.000 |
|
|
Tilleggsopplysninger:
Varelager 6.000.000 4.000.000
Kundefordringer 8.000.000 12.000.000
Leverandørgjeld 14.000.000 10.000.000
Varekostnad 31.000.000
Avskrivninger 11.000.000
Gevinst ved salg av brukte
anleggsmidler 120.000
Hvor mye ble avsatt til utbytte per 31.12.20×1? Oppgi svaret (kun tallet) i kroner og bruk punktum som tusenskiller. Det har ikke vært innskudd av ny egenkapital i løpet av året.
Vi har tidligere sett på denne sammenhengen, som kan brukes til veldig mye.
IB + tilkomst – avgang = UB
For den som trenger å få det inn med teskje. Det denne ligninga sier er:
Så mye hadde jeg (IB) + så mye fikk jeg (tilkomst) – så mye ga jeg bort (avgang) = så mye har jeg igjen (UB).
Tilkomst er det som gjør at beholdningen/balanseposten blir større.
Avgang er det man kvitter seg med, og som følgelig gjør at beholdningen eller balanseposten blir mindre.
Denne kan også brukes her, og da må vi spørre oss selv, hva er “tilkomsten” og “avgangen” her?
Hvordan er det vi får tilkomst til egenkapitalen? Jo, egenkapitalen vokser hvis vi får et positivt resultat, og/eller hvis man får skutt inn egenkapital fra investorer.
Hvordan får vi “avgang”? Jo, egenkapitalen vil krympe hvis selskapet gir ut utbytte til eierne, eller ved underskudd i driften. Derfor blir sammenhengen slik:
IB EK + resultat + innskutt egenkapital – avsatt utbytte = UB EK
Løs denne ligningen med hensyn på avsatt utbytte.
Oppgaven sier ikke noe om innskutt egenkapital, så denne antar vi at er 0.